Skip to main content
NCBI home page
Genetics logoLink to Genetics
. 2006 Nov;174(3):1441–1453. doi: 10.1534/genetics.105.052019

Evolution of the Human Immunodeficiency Virus Envelope Gene Is Dominated by Purifying Selection

C T T Edwards *,1, E C Holmes †, O G Pybus ‡, D J Wilson §, R P Viscidi **, E J Abrams ††, R E Phillips *, A J Drummond ‡,2
PMCID: PMC1667091  PMID: 16951087

Abstract

The evolution of the human immunodeficiency virus (HIV-1) during chronic infection involves the rapid, continuous turnover of genetic diversity. However, the role of natural selection, relative to random genetic drift, in governing this process is unclear. We tested a stochastic model of genetic drift using partial envelope sequences sampled longitudinally in 28 infected children. In each case the Bayesian posterior (empirical) distribution of coalescent genealogies was estimated using Markov chain Monte Carlo methods. Posterior predictive simulation was then used to generate a null distribution of genealogies assuming neutrality, with the null and empirical distributions compared using four genealogy-based summary statistics sensitive to nonneutral evolution. Because both null and empirical distributions were generated within a coalescent framework, we were able to explicitly account for the confounding influence of demography. From the distribution of corrected P-values across patients, we conclude that empirical genealogies are more asymmetric than expected if evolution is driven by mutation and genetic drift only, with an excess of low-frequency polymorphisms in the population. This indicates that although drift may still play an important role, natural selection has a strong influence on the evolution of HIV-1 envelope. A negative relationship between effective population size and substitution rate indicates that as the efficacy of selection increases, a smaller proportion of mutations approach fixation in the population. This suggests the presence of deleterious mutations. We therefore conclude that intrahost HIV-1 evolution in envelope is dominated by purifying selection against low-frequency deleterious mutations that do not reach fixation.

DURING chronic human immunodeficiency virus (HIV-1) infection the turnover of virions is rapid (Ho et al. 1995; Wei et al. 1995), the mutation rate high (Mansky and Temin 1995), and the population size large (Haase 1999). Consequently a huge amount of diversity accumulates (Wain-Hobson 1993), so that viral genomes within an individual can differ by between 3 and 5% in their envelope regions (Balfe et al. 1990; Wolfs et al. 1990; Lamers et al. 1993). This variation has important consequences, allowing HIV-1 to infect different cell types (Groenink et al. 1992; Chavda et al. 1994), evade the immune system (Burns et al. 1993; Price et al. 1997; Wei et al. 2003), and acquire resistance to antiviral drugs (Fitzgibbon et al. 1993; Condra et al. 1996; de Jong et al. 1996). During chronic intrahost infection, the HIV-1 envelope gene diverges from the founding population at a rate of ∼1%/year (Shankarappa et al. 1999). Revealing the processes that govern this diversification, and the properties of mutations that contribute to increasing levels of diversity, is therefore central to our understanding of HIV-1 evolution.

The trajectory of emergent mutations in the population is potentially influenced by both random genetic drift and natural selection. If selection played no role then evolution would proceed according to a stochastic model of genetic drift. With increasing selection, the accumulation of polymorphisms becomes more predictable. When selection is strong and the effect of drift negligible, evolution can be considered deterministic. In between the extremes of deterministic and purely stochastic evolution, it is possible for drift, selection, and mutation to all have interacting and important influences on population evolution (Rouzine et al. 2001).

The degree of evolutionary stochasticity to which a population is subjected is critically influenced by the number of replicating virions N. If the population were ideal (all changes are neutral, with discrete generations and no population subdivision) then stochasticity could be predicted by N, with large N (Nμ ≫ 1; where μ is the mutation rate) associated with a deterministic outcome. Because real populations are not ideal, stochasticity is instead represented by the effective population size Ne, which is the expected value of N under ideal conditions, given the stochasticity observed (Wright 1931). In HIV-1, Ne is typically estimated to be ∼103–104 (Leigh Brown 1997; Seo et al. 2002; Achaz et al. 2004; Shriner et al. 2004). These small Ne values (Neμ ≪ 1) have been interpreted as evidence for stochastic evolution (Leigh Brown 1997; Shriner et al. 2004). However, in each case Ne was obtained under the assumption of neutrality, despite the potential influence that selection may have on its estimation. Because selection is confounded with Ne, Ne does not provide an accurate predictor of stochastic evolution. Instead, it should be regarded simply as a measure of sequence diversity in the population θ, weighted by 1/2μ (i.e., Ne = θ/2μ in a haploid population). Hence, because diversity can be reduced by selection, a low estimated Ne could also be a sign of deterministic evolution in the form of a mutation–selection balance. Arguments have been forwarded that a neutral model of evolution is indeed valid (Leigh Brown 1997; Shriner et al. 2004), so that a low Ne provides an indication of stochasticity. However, by considering individual time points from a single population separately, these have suffered from a lack of statistical power to reject neutrality and nonindependence.

Here we test directly for a stochastic model of evolution in which the fate of emergent mutations is dictated only by genetic drift. Rejecting this model, we infer it to be an inadequate representation of HIV-1 envelope evolution and conclude an important role for natural selection.

We apply our test to envelope sequences from a cohort of HIV-1-infected children, sampled longitudinally from birth. The external envelope protein is a likely site of selection, being targeted by the patient's antibody response (Moore et al. 1994), and responsible for receptor binding and entry into host cells (Wyatt and Sodroski 1998), and therefore constitutes an ideal region with which to investigate the evolutionary processes acting on HIV-1.

MATERIALS AND METHODS

Background:

Currently the best evidence of a role for natural selection in HIV-1 evolution is provided by estimates of the ratio of nonsynonymous to synonymous changes per site (dN/dS), with dN/dS = 1 being the expectation under neutrality. Codon-based estimates of the dN/dS ratio in HIV-1 envelope sequences have consistently shown a preponderance of constrained sites (dN/dS < 1), punctuated by relatively frequent positive selection (dN/dS > 1) (Nielsen and Yang 1998; Ross and Rodrigo 2002; Guindon et al. 2004). These techniques are sensitive to recombination, which leads to an overestimation of the number of positively selected sites (Anisimova et al. 2003; Shriner et al. 2003). Recently a coalescent approximation has been proposed to overcome this problem (Wilson and McVean 2006). However, whether all synonymous changes in HIV-1 are selectively neutral is still uncertain.

Another approach is provided by population genetic arguments based on the frequency distribution of polymorphic sites. The most popular of these tests are Tajima's D (Tajima 1989), and Fu and Li's D (Fu and Li 1993). These compare the contributions of low- and high-frequency polymorphisms to population diversity, representing recent and established substitutions, respectively. The frequency distribution of nonneutral segregating sites will be influenced by selection. Purifying and directional positive selection will lead, on average, to an excess of low-frequency polymorphisms in the contemporary population. However, this pattern of polymorphism can also be produced by demographic change, most notably exponential growth, necessitating the careful application of these statistics.

Because of its sensitivity to selection, we focus on Fu and Li's D as a test statistic, adopting a genealogy-based approach to its estimation. We call this the genealogical D, estimated using a version of coalescent theory (Kingman 1982a,b) that can consider sequences obtained from multiple time points simultaneously (Rodrigo and Felsenstein 1999). This increases the power of our test and removes the problem of nonindependence of samples obtained sequentially from a single individual.

In addition to the genealogical D we include measures of tree symmetry. Selection is likely to leave its mark on the genealogy by biasing the extinction and branching rates of different lineages (Grenfell et al. 2004). This will lead to imbalance, or asymmetry, in the phylogeny (Kirkpatrick and Slatkin 1993), so that the use of measures of tree asymmetry in this study is justified.

Estimates of each test statistic involve sampling a large number of genealogies within a Bayesian framework. Hence, uncertainties in parameters of the evolutionary model and the ancestral genealogy are explicitly acknowledged. For each test of neutrality, a distribution of coalescent genealogies was produced from the empirical data and compared to a simulated null distribution using a goodness-of-fit test.

Testing a model of genetic drift:

Generating the null and posterior genealogical distributions:

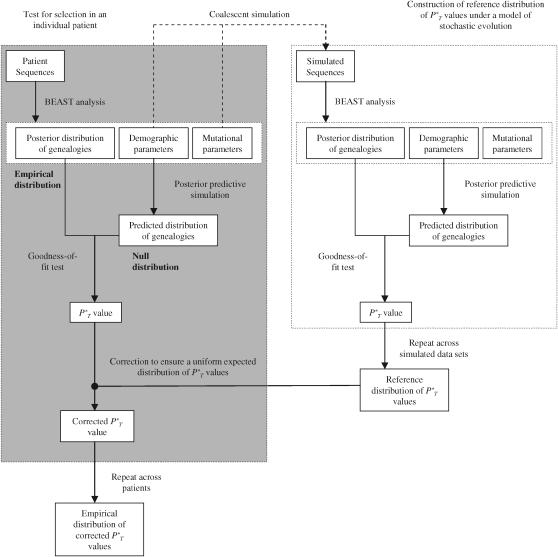
For each set of longitudinally sampled patient sequences the posterior distributions of genealogies were generated using the BEAST software package (Drummond and Rambaut 2004). This selects genealogies according to their posterior probability within a Bayesian framework using Markov chain Monte Carlo (MCMC), as described previously (Drummond et al. 2002). The HKY85 model of nucleotide substitution (Hasegawa et al. 1985), with a four-category discrete approximation to a gamma distribution of rate heterogeneity across sites (Yang 1994), was implemented. All substitution model parameters, including κ, the shape parameter α, and substitution rate μ in changes per site per day, were estimated from the data using MCMC along with demographic model parameters (shaded area in Figure 1). Both a constant population size and exponential growth were assumed. Using the serial sampled coalescent, population size is considered as the product of the effective population size and generation length in days Neτ (Rodrigo and Felsenstein 1999). HIV-1 is known to follow a reproducible pattern of increasing diversity during the course of infection (Shankarappa et al. 1999), making the exponential model appropriate. It was compared to the constant alternative according to the Akaike information criteria (AIC) (Akaike 1973), with the model with the lowest AIC score considered to be the best representation of the data.

Figure 1.—

Figure 1.—

Open in a new tab

Illustrative summary of methods. The procedure outlined was repeated for both constant and exponential demographic models. Further details are given in the appendix.

During MCMC a marginal posterior distribution of genealogies is generated, with each genealogy associated with demographic model parameter values that can be used to predict future iterations of the evolutionary process. This is known as posterior predictive simulation (Rubin 1984), performed here using the COALGEN program (Rambaut and Drummond 2004). It proceeds by simulating new coalescent genealogies using the posterior distribution of demographic parameter values generated from the data, with one simulated tree for each step in the MCMC chain (see Bollback 2002). This generates an appropriate null distribution to test if the assumptions made by the coalescent are accurate, because under this condition the posterior and null distributions are expected to be identical in the long run.

The neutral coalescent proceeds according to a stochastic model that represents an evolutionary process dominated by genetic drift. We are interested in departures from this assumption that are attributable to natural selection. We therefore compared the null and posterior distributions in goodness-of-fit tests using genealogy-based statistics sensitive to nonneutral evolution. One of these statistics, the genealogical D, is also sensitive to demography. In particular, exponential growth is known to lead to more negative values, so that if the null distribution was generated under the incorrect assumption of a constant population size, it would yield a large discrepancy between the posterior and null distribution of values even for a population not influenced by selection. An advantage of posterior predictive simulation is that it can incorporate the assumption of exponential growth so that its potentially confounding influence is explicitly accounted for.

Comparing the null and posterior genealogical distributions:

The observed and predicted genealogical distributions were compared using four summary statistics (Table 1). The genealogical D-statistic is a corrected comparison of the total length of the rooted tree to that expected from the length of the tips under neutral genetic drift (see appendix), and assuming that all sequences were sampled simultaneously (i.e., the neutral expectation for synchronous sequences is 0). When longitudinal samples are considered, the genealogical D is usually <0, even for a neutral population, because the length of internal branches is shortened relative to that predicted from the tips. If slightly deleterious mutations are abundant in the population and selected against, then they will on average be at lower frequency than other mutations (Nielsen and Weinreich 1999) and segregate near to the tips of the genealogy (Williamson and Orive 2002). Simulation studies, in which singleton mutations were randomly allocated to sequences generated under a neutral model of evolution, showed that the presence of low-frequency mutations leads to more negative D-values (data not shown). Positive selection on the other hand is more likely to lead to the fixation of changes between time points (Williamson 2003) and less negative estimates of D. As noted above, the genealogical D is sensitive to exponential growth, which was factored out of the analysis when evidence for exponential growth was detected in the empirical data (i.e., when the exponential demographic model was found to have the lowest AIC score).

TABLE 1.

Summary statistics used to test for selection

Summary statistic Expectation under selection Reference
Genealogical D More negative values indicate purifying selection. —
Less negative values indicate positive directional selection.
B1 Value will decrease as asymmetry increases. Kirkpatrick and Slatkin (1993)
Colless tree imbalance Ic Increases from 0 to 1 as asymmetry increases. Colless (1982)
Cherry count Cn Value will decrease as asymmetry increases. McKenzie and Steel (2000)
Open in a new tab

In addition, three measures of tree symmetry were used: B1 (Kirkpatrick and Slatkin 1993), Colless tree imbalance (Ic) (Colless 1982), and cherry count (Cn) (McKenzie and Steel 2000). The response of each of these statistics to increasing asymmetry is listed in Table 1, with mathematical definitions given in the appendix.

Testing for significance:

To test for a statistically significant difference between the null and posterior genealogical distributions (Figure 1), we first calculated the proportion of times that the simulated genealogy yielded a summary statistic (T) value greater (for Ic) or less (for D, B1, and Cn) than the genealogy estimated from the empirical data. This provided the posterior predictive P-value P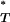Inline graphic (see appendix). In the case of the genealogical D, this specifically tests the significance of more negative values, which would indicate an excess of low-frequency polymorphisms and be consistent with the action of purifying selection.

By considering the entire distributions of T-values in our estimation of P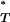Inline graphic, we account for the considerable uncertainty inherent in estimates of the true genealogy. However, posterior predictive P-values are known to be conservative (Meng 1994), in that they do not reveal the full discrepancy between the model being tested and the empirical data. Statistically, there are fewer extreme values than would be expected if P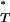Inline graphic followed a uniform reference distribution between 0 and 1. To overcome this problem we simulated multiple sequence data sets under a neutral coalescent model of evolution. By estimating P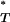Inline graphic for each, we obtained the expected reference distribution of P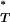Inline graphic-values. This allowed us to apply the appropriate correction to P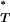Inline graphic-values obtained from the empirical data (see appendix), ensuring that the expected distribution of corrected P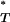Inline graphic-values was uniform. We thus not only increased the sensitivity of our test, but also were able to combine corrected P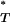Inline graphic-values across patients so that a more powerful inference could be made.

Because we have prior knowledge of the effect of selection on each of the statistics, a one-tailed test was applied to each corrected P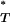Inline graphic-value, with P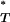Inline graphic < 0.05 considered significant.

Patient data:

Envelope sequences were obtained from 28 HIV-1-positive children infected at birth. The majority of these sequences have been published previously (Edwards et al. 2006) and detailed descriptions of the cohort (Thomas et al. 1994; Abrams et al. 1995) and sequencing techniques (Strunnikova et al. 1995) are given elsewhere.

The sequences analyzed were derived from a heteroduplex mobility assay (HMA), which screens the sample to isolate distinct clones. They were therefore more divergent than would be expected from a random sample. Because closely related sister taxa were underrepresented, the sampled distribution of coalescent times may have been slightly biased toward the past, in comparison to that expected from a random sample. This will have had an effect on estimates of population demography, contributing to the appearance of an expanding or logistically growing population. However, it is unlikely to have affected our test for selection, since the distribution of node heights is accounted for by the demographic correction implemented.

Sequences were ∼360 bp in length, spanning the highly variable envelope V3 region. Multiple clones were available from serial time points postinfection (supplemental Table 1 at http://www.genetics.org/supplemental/) with the majority during the chronic stages of disease (supplemental Table 2 at http://www.genetics.org/supplemental/). All sequences (excepting those from pa, pb, pc, and pd) were derived from viral RNA. These sequences are available from GenBank under accession nos. AY823998–AY824946.

RESULTS

Application of test statistics to patient data:

We tested for departures from a model of genetic drift through the application of each test statistic to envelope sequences from 28 infected children, sampled longitudinally from birth. In the majority of cases (19/28) evidence for exponential growth of the viral population was detected (Table 2). Notable exceptions were the patients for which only proviral DNA was available. Sequences derived from this source will represent virus that may have been active some time in the past. However, the serial sampled coalescent will treat each sequence as a member of the temporal population from which it was sampled. Therefore, because the population may have remained apparently unchanged, it could appear to follow a constant demographic. This suggests that caution should be exercised in interpreting the results from these patients, because unaccounted for exponential growth may have taken place.

TABLE 2.

P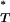Inline graphic-values from tests for a significant departure from a neutral stochastic model of evolution in HIV-1 envelope sequences

Genealogical D
B1
Ic
Cn
Patient data Preferred demographic modela Correctedc
Corrected
Corrected
Corrected
dN/dS ratiod
Uncorrectedb No rec. Rec. Uncorrected No rec. Rec. Uncorrected No rec. Rec. Uncorrected No rec. Rec.
p1 Exponential 0.683 0.608 0.620 0.386 0.333 0.170 0.450 0.500 0.580 0.471 0.333 0.120 0.720
p2 Constant 0.107 0.157 0.444 0.399 0.324 0.323 0.265 0.176 0.253 0.568 0.441 0.424 0.492
p3 Constant 0.031* 0.059 0.091 0.202 0.059 0.051 0.225 0.127 0.222 0.375 0.147 0.111 1.123
p4 Exponential 0.300 0.098 0.170 0.465 0.529 0.340 0.440 0.471 0.540 0.597 0.529 0.380 0.515
p5 Exponential 0.757 0.745 0.710 0.612 0.814 0.670 0.471 0.520 0.610 0.734 0.794 0.700 0.445
p6 Constant 0.045* 0.078 0.172 0.318 0.216 0.152 0.225 0.127 0.222 0.484 0.294 0.253 0.446
p7 Exponential 0.080 0.010* 0.020* 0.238 0.176 0.020* 0.121 0.039* 0.080 0.451 0.294 0.110 1.059
p8 Constant 0.034* 0.069 0.101 0.237 0.098 0.091 0.218 0.127 0.212 0.474 0.294 0.232 0.587
p9 Exponential 0.244 0.039* 0.130 0.172 0.059 0.010* 0.167 0.088 0.170 0.271 0.098 0.010* 0.344
p10 Exponential 0.163 0.010* 0.070 0.633 0.843 0.730 0.316 0.304 0.350 0.698 0.735 0.590 0.868
p11 Exponential 0.103 0.010* 0.040* 0.242 0.186 0.020* 0.153 0.088 0.150 0.397 0.216 0.040* 0.457
p12 Exponential 0.312 0.108 0.180 0.404 0.373 0.200 0.216 0.167 0.230 0.599 0.529 0.380 0.913
p13 Exponential 0.029* 0.010* 0.010* 0.269 0.196 0.030* 0.109 0.029* 0.050 0.584 0.510 0.360 0.462
p14 Exponential 0.215 0.029* 0.100 0.514 0.637 0.460 0.218 0.167 0.230 0.693 0.706 0.580 0.793
p15 Exponential 0.108 0.010* 0.050 0.560 0.755 0.540 0.366 0.373 0.420 0.541 0.392 0.210 0/546
p16 Exponential 0.224 0.029* 0.100 0.426 0.402 0.240 0.514 0.569 0.670 0.508 0.363 0.160 0.402
p18 Constant 0.183 0.235 0.657 0.569 0.598 0.687 0.289 0.186 0.333 0.639 0.618 0.576 0.373
p19 Exponential 0.147 0.010* 0.070 0.438 0.451 0.260 0.134 0.069 0.100 0.678 0.696 0.550 0.463
p20 Exponential 0.405 0.186 0.250 0.483 0.569 0.410 0.449 0.500 0.580 0.650 0.647 0.500 0.305
p21 Exponential 0.378 0.157 0.220 0.501 0.608 0.440 0.270 0.275 0.330 0.650 0.647 0.500 0.573
p22 Exponential 0.606 0.441 0.470 0.545 0.735 0.520 0.481 0.529 0.630 0.694 0.716 0.590 0.276
p23 Exponential 0.115 0.010* 0.050 0.557 0.745 0.530 0.062 0.020* 0.040* 0.776 0.843 0.790 0.442
p24 Exponential 0.146 0.010* 0.070 0.613 0.814 0.670 0.279 0.275 0.330 0.708 0.755 0.630 0.312
p25 Exponential 0.075 0.010* 0.020* 0.073 0.010* 0.010* 0.126 0.049* 0.090 0.170 0.020* 0.010* 0.727
pa Constant 0.003* 0.010* 0.010* 0.409 0.333 0.333 0.381 0.304 0.485 0.470 0.255 0.212 0.591
pb Constant 0.001* 0.010* 0.010* 0.136 0.020* 0.030* 0.097 0.049* 0.061 0.322 0.108 0.061 0.569
pc Constant 0.003* 0.010* 0.010* 0.200 0.049* 0.051 0.168 0.098 0.162 0.324 0.108 0.071 0.747
pd Constant 0.027* 0.059 0.061 0.318 0.216 0.152 0.215 0.127 0.212 0.491 0.294 0.253 0.314
Open in a new tab
*

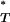PInline graphic-values significant at the 5% level.

a

The best-fit (preferred) demographic model selected using the Akaike information criteria.

b

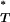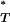Uncorrected PInline graphic-values.

c

PInline graphic-values corrected using a reference distribution that assumes either no recombination (No rec.) or recombination (Rec.).

d

Estimated across the entire genetic region using maximum likelihood according to the method of Goldman and Yang (1994).

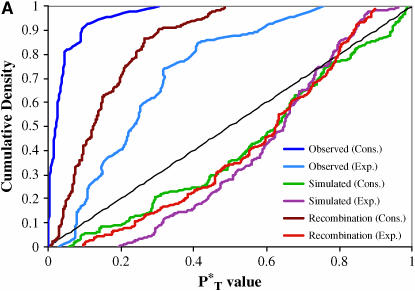
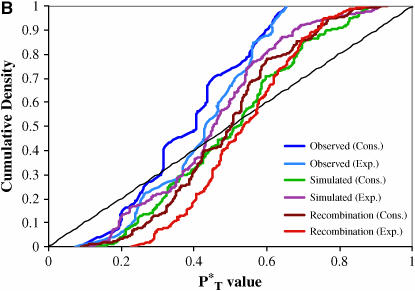
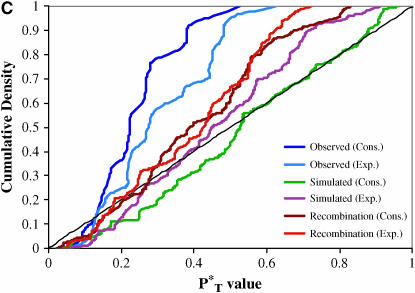
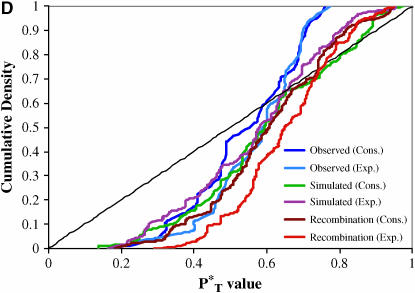
The distributions of uncorrected P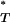Inline graphic-values across patients, assuming both a constant and an exponential demographic, are shown in Figure 2. Also shown are the reference distributions of P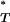Inline graphic-values obtained from sequences simulated under a neutral coalescent model (see appendix). These are typically S-shaped, rather than lying on the diagonal, consistent with the conservative nature of posterior predictive P-values (i.e., there is a lower frequency of extreme values than would be expected from a uniform distribution). After correcting P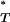Inline graphic-values with the simulated reference distributions, and assuming the best-fit (preferred) demographic model, we obtained significant results using both the genealogical D and measures of tree asymmetry (Table 2). The genealogical D gave the strongest evidence for selection, with 15 of the patients tested giving significant corrected P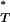Inline graphic-values (Table 2).

Figure 2.—

Figure 2.—

Figure 2.—

Figure 2.—

Figure 2.—

Open in a new tab

Distribution of uncorrected P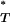Inline graphic-values for each test statistic, calculated using the observed data. Also shown are the reference distributions of P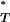Inline graphic-values from data simulated under constant and exponential demographic models, with and without recombination. (A) Genealogical D. (B) B1. (C) Colless tree imbalance Ic. (D) Cherry count Cn.

Accounting for recombination:

The posterior distributions of genealogies were generated assuming no recombination. If recombination is not accounted for, the resultant homoplasious changes will lead to a lengthening of the tips of the genealogy relative to the internal branches, in a manner similar to exponential growth (Schierup and Hein 2000). It also has the potential to affect tree asymmetry. Because recombination in HIV-1 is frequent (Jung et al. 2002; Zhuang et al. 2002), it may therefore have influenced our estimation of each test statistic. In particular, our estimate of the genealogical D will be biased toward more negative values if sequences were obtained from a recombining population. To account for the potential influence of recombination on our estimates of D and tree asymmetry, we simulated reference distributions under this assumption and used them to correct our P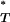Inline graphic-values.

For each patient we first estimated the per site rate of recombination using the LDhat software package (McVean et al. 2002). Because of the short sequence length, we assumed a linear model of recombination. The significance of each result was tested using the Lkmax test, which randomly permutes segregating sites along the sequence and tests whether the maximum composite likelihood obtained from the real data differs from this null distribution. The average ratio of the recombination to mutation rate (r/μ) was found to be 0.44 (range 0.0–3.3) (supplemental Table 3 at http://www.genetics.org/supplemental/). Sequences were then generated as before assuming both a constant population size and exponential growth, with an r/μ ratio of 0.5 (approximately equal to the mean across data sets).

If the reference distributions of P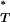Inline graphic-values obtained with and without recombination are different, this indicates that recombination may have confounded interpretation of our significant results. Using the Kolmogorov–Smirnov test we found significant differences in the reference distributions of P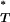Inline graphic-values for all statistics (Figure 2 and Table 3). This indicated that our original correction to empirical P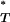Inline graphic-values may not have been robust to the effect of recombination. In the case of the genealogical D, recombination leads to more negative values, so that the significance of P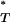Inline graphic-values will have been increased (see reference distributions in Figure 2). Interestingly, this bias was much greater when a constant population size was assumed. In the case of tree asymmetry, the effect of recombination was also dependent on the demographic model assumed (Table 3). The reasons for this are unclear, since recombination is likely to have broad and unpredictable effects on the inferred genealogy. Nevertheless, we consider there to be sufficient evidence to necessitate a correction for its effect. We therefore applied a new correction based on reference distributions constructed under the assumption of recombination. This ensured that recombination was taken into account when interpreting the significance of our results.

TABLE 3.

Kolmogorov–Smirnov tests for equivalence of reference distributions in presence vs. absence of recombination

P-value
Demographic model D B1 Ic Cn
Constant size <0.001* 0.557 0.004* 0.712
Exponential growth 0.527 0.009* 0.034* 0.010*
Open in a new tab
*

Kolmogorov–Smirnov P-values significant at the 5% level.

For the genealogical D, we found a notable reduction in the significance of our results under the preferred demographic model (Table 2). This indicated that significant departures from a simple stochastic model of evolution could have been induced by an empirically relevant rate of recombination. Furthermore, in four of the seven patients for which significant results were still observed (p11, p13, pa, and pb) r/μ ratios >0.5 were estimated (supplemental Table 3 at http://www.genetics.org/supplemental/). For these patients correction for the effects of recombination may have been inadequate.

The effect of recombination on measures of tree asymmetry was more complex. For Ic the number of significant results was also reduced, again indicating that recombination can inflate the significance of departures from the expectation under drift, in this case by increasing levels of asymmetry. The correction applied lowered the significance of observed Ic-values to take this effect of recombination into account. In contrast, for B1 and Cn the number of significant results was increased. This can be explained if recombination lowered the degree of asymmetry recorded by these measures, so that the significance of observed values of B1 and Cn was increased when recombination was taken into account.

Even after correction for recombination a number of significant results remained (Table 2). Because the statistics applied were specifically designed to detect nonneutral evolution, and because their significance cannot be accounted for by demography, we interpreted this as evidence for selection.

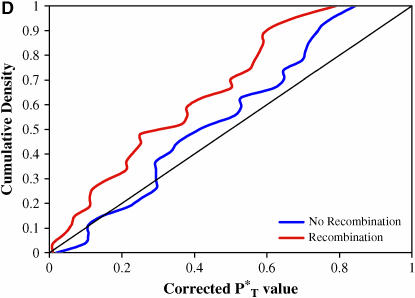
Distribution of PT*-values across patients:

To improve the sensitivity of our analysis we next examined the distribution of corrected P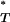Inline graphic-values across patient data sets for evidence of a role for natural selection in HIV-1 evolution. Departures from the expected uniform distribution were assessed using a one-tailed 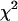Inline graphic-test (see appendix).

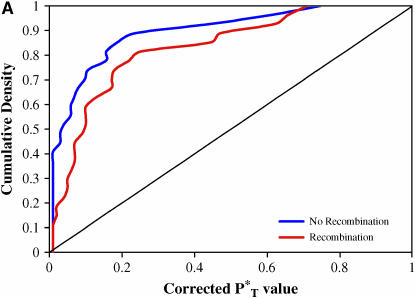
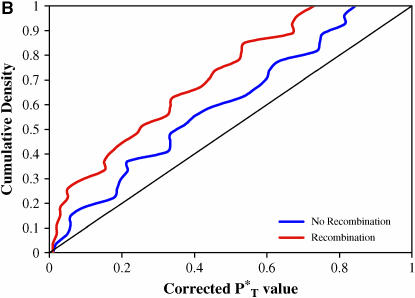
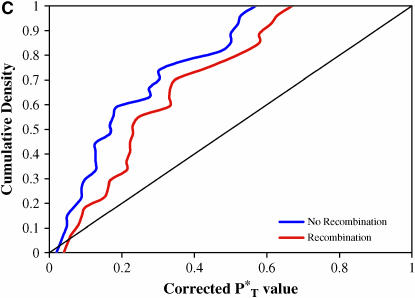
We found our results to be highly significant. Figure 3 shows the distribution of corrected P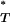Inline graphic-values across patients, with corrections applied using a reference distribution with and without recombination. For purposes of illustration, only P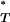Inline graphic-values obtained assuming the preferred demographic model for each patient are shown. The significance of departures from the expected uniform distribution is listed in Table 4. Assuming recombination, and under the preferred demographic model, all statistics yielded a significant result.

Figure 3.—

Figure 3.—

Figure 3.—

Figure 3.—

Figure 3.—

Open in a new tab

Distribution of corrected P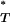Inline graphic-values for each test statistic, assuming the preferred demographic model, with and without recombination. The diagonal line represents the uniform distribution expected if sequences evolved according to a neutral stochastic model. (A) Genealogical D. (B) B1. (C) Colless tree imbalance Ic. (D) Cherry count Cn.

TABLE 4.

Tests for selection using the distribution of corrected P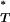Inline graphic-values across patients

P-value
Reference distribution D B1 Ic Cn
No recombination
Constant size <0.001* 0.015* <0.001* 0.350
Exponential growth <0.001* 0.422 0.011* 0.786
Preferred model <0.001* 0.053* <0.001* 0.442
Recombination
Constant size <0.001* 0.010* 0.015* 0.097
Exponential growth <0.001* <0.001* 0.146 0.020*
Preferred model <0.001* <0.001* 0.035* 0.014*
Open in a new tab

P-values indicate the significance of departure from the uniform expectation and were calculated as outlined in the appendix. *Values significant at the 5% level.

The presence of slightly deleterious mutations:

More negative genealogical D-values, compared to the expectation under neutral genetic drift, indicate an excess of low-frequency polymorphisms in the population. Because positive selection is likely to fix changes between time points, leading to a deficiency of low-frequency polymorphisms, this result suggests that these represent transient, slightly deleterious mutations that are removed from the population by purifying selection before they increase in frequency.

To gain further insight into the nature of the selective forces operating we estimated the overall dN/dS ratio across the region using a codon-based method (Goldman and Yang 1994). This provides an appropriate comparison to the results presented here. In line with previous work on HIV-1 envelope (Nielsen and Yang 1998), the overall dN/dS ratio is <1 for all patients (except p3 and p7). These results do not in themselves provide a robust test of selection, but nevertheless indicate that if selection is acting, as we have argued here, its primary role is in lowering the rate of nonsynonymous substitution.

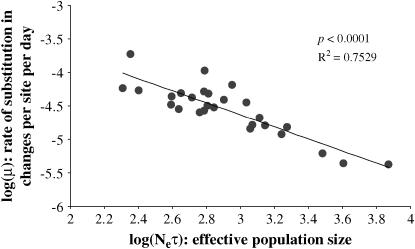
If the majority of mutations are slightly deleterious, then purifying selection will lower their contribution to the substitutions that occur between time points. Therefore the stronger the selection, the lower the rate of fixation (Kimura 1962). To investigate the relationship between the strength of selection and rate of substitution we plotted μ against the effective population size Neτ, both estimated using BEAST. Because estimates of Neτ will be influenced by selection (as discussed above), it was obtained using the third codon site only. The majority (∼70%) of changes at this position are synonymous, so that diversity is more likely to reflect the strength of selection acting on the population.

Under a strictly neutral model of sequence evolution the rate of substitution is dependent only on the underlying mutation rate and is therefore independent of the population size. In contrast to this expectation, we found a strong negative correlation between μ and Neτ (P < 0.0001; Figure 4). This result is consistent with theoretical predictions (Ohta 1987) and suggests the action of purifying selection in removing slightly deleterious mutations from the population before they increase in frequency.

Figure 4.—

Figure 4.—

Open in a new tab

Regression analysis showing a negative correlation between the substitution rate μ and effective population size Neτ, estimated using the third codon position only. The rate of substitution could not be reliably estimated from one patient.

DISCUSSION

We have tested for a stochastic model of evolution in which mutations arise randomly and in proportion to the length of each branch in the coalescent genealogy. This represents evolution driven by mutation and random genetic drift only. Our analysis shows that the empirical data do not fit this model. Because the genealogical statistics used to test model fit were designed specifically to detect nonneutral evolution, we interpret this as evidence for natural selection acting on the population.

Population genetics theory states that genetic drift will dominate evolution when the product of the effective population size and selection coefficient is much less than one (Nes ≪ 1). Because the HIV-1 genome is not strictly neutral (s ≠ 0), this would be interpreted as evidence for a low Ne. We have shown that this is not the case, so that selection is important in shaping the evolution of HIV-1 envelope sequences. This conclusion does not imply that evolution is deterministic with natural selection the only important component. Genetic drift is likely to play a substantial role, particularly at sites where the selection coefficient is small. In the case of purifying selection, evolution may still be considered stochastic but with an increased bias toward the loss (rather than fixation) of emergent mutations.

Our analyses focused on the frequency distribution of polymorphic sites in the population and tree asymmetry, both estimated from the coalescent genealogy. By simulating a null distribution of genealogies under a stochastic model of genetic drift, we could test directly whether the observed frequency distribution differed significantly from this expectation. The approach adopted incorporates a number of improvements on previous tests that have applied similar goodness-of-fit tests (Leigh Brown 1997; Shriner et al. 2004). Multiple time points were considered simultaneously, improving the power of each test and removing nonindependence from the analysis. Furthermore, the use of posterior predictive simulation to generate the null distribution of genealogies eliminated the confounding influence of demographic change. Further improvements to the sensitivity of our test could be made by estimating demography using synonymous sites only. Assuming that synonymous and nonsynonymous sites evolve independently, this would allow posterior predictive simulation under conditions that more closely reflect the actual demography of the viral population. Although these techniques are currently unavailable within the implemented framework, they could provide a fruitful avenue for future research (see Hahn et al. 2002).

In addition to higher than expected levels of tree asymmetry, we found that the frequency distribution of polymorphic sites (summarized by the genealogical D) was significantly different from the expectation under drift, with a clear excess of low-frequency mutations. This suggests that purifying selection acts to remove slightly deleterious mutations before they increase in frequency, an interpretation consistent with codon-based estimates of the dN/dS ratio, both here and in previous work (Nielsen and Yang 1998; Ross and Rodrigo 2002), that show the rate of nonsynonymous substitution is generally low. To further investigate this hypothesis, we plotted the relationship between the rate of substitution μ and effective population size Neτ. We found a strong negative correlation between μ and Neτ, as expected if the majority of mutations are removed from the population and therefore make a decreasing contribution to the overall rate of change as the efficacy of selection increases (Ohta 1987). Because Neτ will be influenced by selection, we considered diversity only at third codon positions, which is largely synonymous. Nevertheless, synonymous diversity may still be reduced through linkage to sites that are under directional positive selection (Maynard Smith and Haigh 1974). Thus, although it would predict a deficiency in the proportion of low-frequency mutations and therefore be incompatible with our previous observations, an alternative explanation of this relationship is that the strength of positive directional selection differs between patients, being strongest at low levels of associated diversity.

A role for frequency-dependent selection is also plausible, so that the fitness advantage of a particular mutation is lost as it increases in frequency, impeding its eventual fixation. The negative relationship could then be explained if strong frequency-dependent selection imposed by the immune response simultaneously increased diversity and lowered the rate of substitution. This, however, would contradict what is known from empirical studies, which show that antibody escape mutations in envelope reach high frequencies before their selective advantage is lost (Wei et al. 2003). Frequency-dependent selection is therefore unlikely to be strong enough to influence our estimates of the substitution rate. Furthermore, there does not appear to be any correlation between vigor of the antibody response and plasma viral loads (Richman et al. 2003; Schmitz et al. 2003), making it unlikely that the strength of frequency-dependent selection will correlate consistently with diversity across patients. On the basis of these arguments we conclude that frequency-dependent selection is an improbable explanation for the negative relation observed between μ and Neτ.

Our results suggest that HIV-1 carries a mutational load of low frequency, deleterious mutations, which represent a substantial contribution to the total genetic diversity of the viral population. A burden of deleterious mutations is a probable consequence of the high rate at which genetic errors are introduced during replication (Mansky and Temin 1995), necessitating a short, compact genome to maintain evolutionary consistency (Overbaugh and Bangham 2001; Holmes 2003). Even in the envelope gene, the most highly variable region of the genome, a degree of constraint is required for operational viability. This is not surprising, given its essential role in receptor binding and cell entry (Wyatt and Sodroski 1998) and the need to maintain extensive glycosylation on its surface to avoid antibody neutralization (Reitter et al. 1998).

Acknowledgments

The BEAST analysis software was developed by Alexei Drummond and Andrew Rambaut and contributed to by Roald Forsberg, Oliver Pybus, and Korbinian Strimmer. We gratefully acknowledge the contribution of the New York City Maternal Infant HIV Transmission Study, funded by the Centers for Disease Control and Prevention. This work was supported by the Wellcome Trust (C.E., A.D., R.P., and E.H.) and the Biotechnology and Biological Sciences Research Council (D.W.).

APPENDIX

Mathematical definitions of genealogy-based statistics for testing nonneutral evolution:

Genealogical D:

Given the number of sequences n, the total length of the genealogy T, and the total length of the external branches Te, the genealogical D is defined as

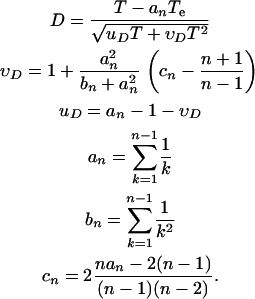graphic file with name M32.gif

The definitions of υD, uD, an, bn, and cn are reproduced directly from Fu and Li (1993).

B1:

Each interior node in a bifurcating genealogy is considered as the root of a subgenealogy. M is the maximum number of interior nodes between each root i and the terminal branches. This is summed over all interior nodes, excluding the root for the entire genealogy:

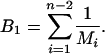graphic file with name M33.gif

Colless tree imbalance Ic:

For each of n − 1 internal nodes in a bifurcating genealogy, sequences are partitioned into two groups of sizes ri and si, with ri ≥ si. Ic is based on the differences between ri and si summed over all internal nodes:

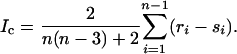graphic file with name M34.gif

Cherry count Cn:

A cherry is defined simply as a pair of sequences adjacent to a single common ancestor node on the genealogy. The number of cherries gives the cherry count Cn.

Testing for neutrality in serially sampled genetic sequences from a single viral population:

Estimation of genealogy and demographic parameters:

Two demographic models, namely constant population size and exponential growth, were fitted to sequences from each patient using the BEAST program (Drummond and Rambaut 2004). This applies a Bayesian coalescent framework using MCMC, with all substitution and demographic parameters estimated from the data and values represented by their marginal posterior probability distributions. All priors were assumed to be uniform on a natural scale. In this way a distribution of genealogies was generated around the posterior expectation, with each genealogy associated with a vector of mutational and demographic model parameters (Drummond et al. 2002). This is referred to in the text as the “empirical” posterior distribution.

Model fit:

The relative fit of each demographic model to the data was assessed using the AIC (Akaike 1973). The AIC of a given model is twice its marginal log likelihood plus the number of parameters specified (AIC = 2 lnLk + 2p). The model with the lowest AIC was selected as the best representation of the data.

Simulation of the null distribution:

The posterior distributions of demographic model parameters, namely the product of effective population size and generation length in days (Neτ) (see Rodrigo and Felsenstein 1999) and growth rate r, were then used to simulate new genealogies in a neutral coalescent process. One new genealogy was produced for each genealogy in the empirical posterior distribution. This is known as posterior predictive simulation (Rubin 1984) and effectively produces a null distribution of genealogies under the coalescent model that can be compared to the empirical distribution in a goodness-of-fit test. This tests for violations of the assumptions made by the coalescent.

Comparison of null and empirical distributions:

To test for departures from the neutral coalescent model we compared the “empirical” posterior distribution and “null” predicted distribution of genealogies in a goodness-of-fit test using descriptive statistics (referred to here as T). The posterior predictive P-value is

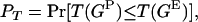graphic file with name M35.gif (A1)

where T(GP) is the value of T given by a predicted genealogy and T(GE) is that by an empirical genealogy. PT can be obtained using a consistent estimator as the proportion of times that the predicted genealogy yields a value of T less than the genealogy estimated from the real data,

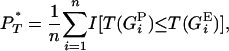graphic file with name M36.gif (A2)

where the indicator function I(.) takes the value 1 when its argument is true and 0 otherwise. By considering the entire distribution of T-values, P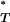Inline graphic accounts for the considerable uncertainty inherent in estimates of the true genealogy. Note that the direction of the inequality is dependent on the statistic used. Equations A1 and A2 are appropriate for the genealogical D, B1, and Cn. Selection leads to a reduction in the value of these test statistics (Table 1). Significance is therefore obtained when P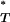Inline graphic < 0.05. The value for Ic, however, is increased by selection. In this case therefore the inequality is reversed.

The need to correct PT*-values:

By convention, P-values are expected to follow a uniform distribution between 0 and 1, so that the type I error rate is equal to the chosen significance level. However, posterior predictive P-values such as P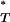Inline graphic are known to be conservative (Meng 1994). Intuitively, this is because the same data are used both to estimate the parameter distributions and to test the goodness-of-fit. Using the uniform distribution as a reference will therefore lead to a conservative test, and it is necessary to obtain a new reference distribution. This can be used to correct our P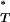Inline graphic-values so that their expectation is indeed uniform.

Simulating the necessary reference distributions:

New reference distributions were obtained by generating sequences using a neutral coalescent simulator. The sampling structure, length of artificial sequences, and mutational and demographic parameters were selected as representative of the patient data. Both a constant population size and exponential growth were assumed. One hundred time-structured data sets were obtained with sample times at 0, 300, 600, and 900 days and 10 sequences at each time. Artificial DNA sequences were 400 bp in length and simulated down the coalescent tree under an HKY + continuous Γ model of substitution with κ = 8.0, α = 0.1, and μ = 4.0 × 10−5/site/day. Insertions and deletions were not simulated. For a constant population size, Neτ was set to 1500. For data sets simulated under exponential growth, Neτ was 5000 and the growth rate 2.0 × 10−3.

For each artificial sequence data set produced, a P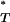Inline graphic-value was estimated. The distribution of these values is shown in Figure 2, which reveals that the expected P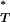Inline graphic is indeed not uniform, with a paucity of extreme values.

Obtaining corrected PT*-values:

If N is the number of data points in the simulated reference distribution and n the number of data points in the reference distribution ≤P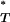Inline graphic, then

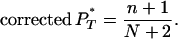graphic file with name M44.gif (A3)

Note that each uncorrected P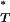Inline graphic was obtained assuming a particular demographic model and corrected using a reference distribution generated under the same demographic assumption.

This procedure allowed us to apply a one-tailed 5% significance test to the corrected P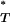Inline graphic-value generated for each test with the expectation of a 5% type I error rate.

Testing for neutrality across multiple-sequence data sets:

Because corrected P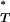Inline graphic-values follow a uniform distribution between 0 and 1, they can be combined across patients, even if obtained under different demographic scenarios. Instead of relying on individual tests of neutrality, this allows for a more powerful inference.

Combining values over all 28 patients, let

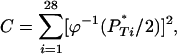graphic file with name M48.gif

where 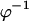Inline graphic is the inverse cumulative distribution function of the standard normal distribution N(0, 1). Under the null model, C follows a 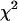Inline graphic-distribution with 28 d.f., so that a one-tailed 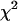Inline graphic-test gives the combined corrected P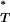Inline graphic-value. This effectively tests whether the empirical distribution of corrected P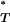Inline graphic-values differs significantly from the uniform expectation (Figure 3 and Table 4).

Sequence data from this article have been deposited with the EMBL/GenBank Data Libraries under accession nos. AY823998–AY824946.

References

  1. Abrams, E. J., P. B. Matheson, P. A. Thomas, D. M. Thea, K. Krasinski et al., 1995. Neonatal predictors of infection status and early death among 332 infants at risk of HIV-1 infection monitored prospectively from birth. New York City Perinatal HIV Transmission Collaborative Study Group. Pediatrics 96: 451–458. [PubMed] [Google Scholar]
  2. Achaz, J., S. Palmer, M. Kearney, F. Maldarelli, J. W. Mellors et al., 2004. A robust measure of HIV-1 population turnover within chronically infected individuals. Mol. Biol. Evol. 21: 1902–1912. [DOI] [PubMed] [Google Scholar]
  3. Akaike, H., 1973. Information theory as an extension of the maximum likelihood principle, pp. 267–281 in Second International Symposium on Information Theory, edited by B. N. Petrov and F. Csaki. Akademiai Kiado, Budapest.
  4. Anisimova, M., R. Nielsen and Z. Yang, 2003. Effect of recombination on the accuracy of the likelihood method for detecting positive selection at amino acid sites. Genetics 164: 1229–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Balfe, P., P. Simmonds, C. A. Ludlam, J. O. Bishop and A. J. Leigh Brown, 1990. Concurrent evolution of human immunodeficiency virus type 1 in patients infected from the same source: rate of sequence change and low frequency of inactivating mutations. J. Virol. 64: 6221–6233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bollback, J. P., 2002. Bayesian model choice and adequacy in phylogenetics. Mol. Biol. Evol. 19: 1171–1180. [DOI] [PubMed] [Google Scholar]
  7. Burns, D. P., C. Collignon and R. C. Desrosiers, 1993. Simian immunodeficiency virus mutants resistant to serum neutralization arise during persistent infection of rhesus monkeys. J. Virol. 67: 4104–4113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chavda, S. C., P. Griffin, Z. Han-Liu, B. Keys, M. A. Vekony et al., 1994. Molecular determinants of the V3 loop of human immunodeficiency virus type 1 glycoprotein gp120 responsible for controlling cell tropism. J. Gen. Virol. 75(11): 3249–3253. [DOI] [PubMed] [Google Scholar]
  9. Colless, D. H., 1982. Phylogenetics: the theory and practice of phylogenetic systematics. Syst. Zool. 31: 100–104. [Google Scholar]
  10. Condra, J. H., D. J. Holder, W. A. Schleif, O. M. Blahy, R. M. Danovich et al., 1996. Genetic correlates of in vivo viral resistance to indinavir, a human immunodeficiency virus type 1 protease inhibitor. J. Virol. 70: 8270–8276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. de Jong, M. D., J. Veenstra, N. I. Stilianakis, R. Schuurman, J. M. Lange et al., 1996. Host-parasite dynamics and outgrowth of virus containing a single K70R amino acid change in reverse transcriptase are responsible for the loss of human immunodeficiency virus type 1 RNA load suppression by zidovudine. Proc. Natl. Acad. Sci. USA 93: 5501–5506. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Drummond, A., and A. Rambaut, 2004. BEAST. Bayesian Evolutionary Analysis Sampling Trees v1.1. (http://evolve.zoo.ox.ac.uk/software.html). [DOI] [PMC free article] [PubMed]
  13. Drummond, A. J., G. K. Nicholls, A. G. Rodrigo and W. Solomon, 2002. Estimating mutation parameters, population history and genealogy simultaneously from temporally spaced sequence data. Genetics 161: 1307–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Edwards, C. T. T., E. C. Holmes, D. J. Wilson, R. P. Viscidi, E. J. Abrams et al., 2006. Population genetic estimation of the loss of genetic diversity during horizontal transmission of HIV-1. BMC Evol. Biol. 6: 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fitzgibbon, J. E., A. E. Farnham, S. J. Sperber, H. Kim and D. T. Dubin, 1993. Human immunodeficiency virus type 1 pol gene mutations in an AIDS patient treated with multiple antiretroviral drugs. J. Virol. 67: 7271–7275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fu, Y. X., and W. H. Li, 1993. Statistical tests of neutrality of mutations. Genetics 133: 693–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Goldman, N., and Z. Yang, 1994. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol. Biol. Evol. 11: 725–736. [DOI] [PubMed] [Google Scholar]
  18. Grenfell, B. T., O. G. Pybus, J. R. Gog, J. L. Wood, J. M. Daly et al., 2004. Unifying the epidemiological and evolutionary dynamics of pathogens. Science 303: 327–332. [DOI] [PubMed] [Google Scholar]
  19. Groenink, M., A. C. Andeweg, R. A. Fouchier, S. Broersen, R. C. van der Jagt et al., 1992. Phenotype-associated env gene variation among eight related human immunodeficiency virus type 1 clones: evidence for in vivo recombination and determinants of cytotropism outside the V3 domain. J. Virol. 66: 6175–6180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Guindon, S., A. G. Rodrigo, K. A. Dyer and J. P. Huelsenbeck, 2004. Modeling the site-specific variation of selection patterns along lineages. Proc. Natl. Acad. Sci. USA 101: 12957–12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Haase, A. T., 1999. Population biology of HIV-1 infection: viral and CD4+ T cell demographics and dynamics in lymphatic tissues. Annu. Rev. Immunol. 17: 625–656. [DOI] [PubMed] [Google Scholar]
  22. Hahn, M. W., M. D. Rausher and C. W. Cunningham, 2002. Distinguishing between selection and population expansion in an experimental lineage of bacteriophage T7. Genetics 161: 11–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hasegawa, M., H. Kishino and T. Yano, 1985. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22: 160–174. [DOI] [PubMed] [Google Scholar]
  24. Ho, D. D., A. U. Neumann, A. S. Perelson, W. Chen, J. M. Leonard et al., 1995. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 373: 123–126. [DOI] [PubMed] [Google Scholar]
  25. Holmes, E. C., 2003. Error thresholds and the constraints to RNA virus evolution. Trends Microbiol. 11: 543–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jung, A., R. Maier, J. P. Vartanian, G. Bocharov, V. Jung et al., 2002. Recombination: multiply infected spleen cells in HIV patients. Nature 418: 144. [DOI] [PubMed] [Google Scholar]
  27. Kimura, M., 1962. On the probability of fixation of mutant genes in a population. Genetics 47: 713–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kingman, M., 1982. a The coalescent. Stoch. Proc. Appl. 13: 235–248. [Google Scholar]
  29. Kingman, M., 1982. b On the genealogy of large populations. J. Appl. Probab. 19A: 27–43. [Google Scholar]
  30. Kirkpatrick, M., and M. Slatkin, 1993. Searching for evolutionary patterns in the shape of a phylogenetic tree. Evolution 47: 1171–1181. [DOI] [PubMed] [Google Scholar]
  31. Lamers, S. L., J. W. Sleasman, J. X. She, K. A. Barrie, S. M. Pomeroy et al., 1993. Independent variation and positive selection in env V1 and V2 domains within maternal-infant strains of human immunodeficiency virus type 1 in vivo. J. Virol. 67: 3951–3960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Leigh Brown, A. J., 1997. Analysis of HIV-1 env gene sequences reveals evidence for a low effective number in the viral population. Proc. Natl. Acad. Sci. USA 94: 1862–1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mansky, L. M., and H. M. Temin, 1995. Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J. Virol. 69: 5087–5094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Maynard Smith, J., and J. Haigh, 1974. The hitch-hiking effect of a favourable gene. Genet. Res. 23: 23–35. [PubMed] [Google Scholar]
  35. McKenzie, A., and M. Steel, 2000. Distributions of cherries for two models of trees. Math. Biosci. 164: 81–92. [DOI] [PubMed] [Google Scholar]
  36. McVean, G., P. Awadalla and P. Fearnhead, 2002. A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics 160: 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Meng, X.-L., 1994. Posterior predictive p-values. Ann. Stat. 22: 1142–1160. [Google Scholar]
  38. Moore, J. P., Y. Cao, D. D. Ho and R. A. Koup, 1994. Development of the anti-gp120 antibody response during seroconversion to human immunodeficiency virus type 1. J. Virol. 68: 5142–5155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nielsen, R., and D. M. Weinreich, 1999. The age of nonsynonymous and synonymous mutations in animal mtDNA and implications for the mildly deleterious theory. Genetics 153: 497–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Nielsen, R., and Z. Yang, 1998. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics 148: 929–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ohta, T., 1987. Very slightly deleterious mutations and the molecular clock. J. Mol. Evol. 26: 1–6. [DOI] [PubMed] [Google Scholar]
  42. Overbaugh, J., and C. R. Bangham, 2001. Selection forces and constraints on retroviral sequence variation. Science 292: 1106–1109. [DOI] [PubMed] [Google Scholar]
  43. Price, D. A., P. J. Goulder, P. Klenerman, A. K. Sewell, P. J. Easterbrook et al., 1997. Positive selection of HIV-1 cytotoxic T lymphocyte escape variants during primary infection. Proc. Natl. Acad. Sci. USA 94: 1890–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Rambaut, A., and A. Drummond, 2004. Coalescent Generator v1.0. (http://evolve.zoo.ox.ac.uk/software.html).
  45. Reitter, J. N., R. E. Means and R. C. Desrosiers, 1998. A role for carbohydrates in immune evasion in AIDS. Nat. Med. 4: 679–684. [DOI] [PubMed] [Google Scholar]
  46. Richman, D. D., T. Wrin, S. J. Little and C. J. Petropoulos, 2003. Rapid evolution of the neutralizing antibody response to HIV type 1 infection. Proc. Natl. Acad. Sci. USA 100: 4144–4149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rodrigo, A. G., and J. Felsenstein, 1999. Coalescent approaches to HIV population genetics, pp. 233–272 in The Evolution of HIV, edited by K. A. Crandall. John Hopkins University Press, Baltimore.
  48. Ross, H. A., and A. G. Rodrigo, 2002. Immune-mediated positive selection drives human immunodeficiency virus type 1 molecular variation and predicts disease duration. J. Virol. 76: 11715–11720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Rouzine, I. M., A. Rodrigo and J. M. Coffin, 2001. Transition between stochastic evolution and deterministic evolution in the presence of selection: general theory and application to virology. Microbiol. Mol. Biol. Rev. 65: 151–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Rubin, D., 1984. Bayesianly justifiable and relevant frequency calculations for the applied statistician. Ann. Stat. 12: 1151–1172. [Google Scholar]
  51. Schierup, M. H., and J. Hein, 2000. Consequences of recombination on traditional phylogenetic analysis. Genetics 156: 879–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Schmitz, J. E., M. J. Kuroda, S. Santra, M. A. Simon, M. A. Lifton et al., 2003. Effect of humoral immune responses on controlling viremia during primary infection of rhesus monkeys with simian immunodeficiency virus. J. Virol. 77: 2165–2173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Seo, T. K., J. L. Thorne, M. Hasegawa and H. Kishino, 2002. Estimation of effective population size of HIV-1 within a host: a pseudomaximum-likelihood approach. Genetics 160: 1283–1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Shankarappa, R., J. B. Margolick, S. J. Gange, A. G. Rodrigo, D. Upchurch et al., 1999. Consistent viral evolutionary changes associated with the progression of human immunodeficiency virus type 1 infection. J. Virol. 73: 10489–10502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Shriner, D., D. C. Nickle, M. A. Jensen and J. I. Mullins, 2003. Potential impact of recombination on sitewise approaches for detecting positive natural selection. Genet. Res. 81: 115–121. [DOI] [PubMed] [Google Scholar]
  56. Shriner, D., R. Shankarappa, M. A. Jensen, D. C. Nickle, J. E. Mittler et al., 2004. Influence of random genetic drift on human immunodeficiency virus type 1 env evolution during chronic infection. Genetics 166: 1155–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Strunnikova, N., S. C. Ray, R. A. Livingston, E. Rubalcaba and R. P. Viscidi, 1995. Convergent evolution within the V3 loop domain of human immunodeficiency virus type 1 in association with disease progression. J. Virol. 69: 7548–7558. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Tajima, F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Thomas, P. A., J. Weedon, K. Krasinski, E. Abrams, N. Shaffer et al., 1994. Maternal predictors of perinatal human immunodeficiency virus transmission. The New York City Perinatal HIV Transmission Collaborative Study Group. Pediatr. Infect. Dis. J. 13: 489–495. [DOI] [PubMed] [Google Scholar]
  60. Wain-Hobson, S., 1993. The fastest genome evolution ever described: HIV variation in situ. Curr. Opin. Genet. Dev. 3: 878–883. [DOI] [PubMed] [Google Scholar]
  61. Wei, X., S. K. Ghosh, M. E. Taylor, V. A. Johnson, E. A. Emini et al., 1995. Viral dynamics in human immunodeficiency virus type 1 infection. Nature 373: 117–122. [DOI] [PubMed] [Google Scholar]
  62. Wei, X., J. M. Decker, S. Wang, H. Hui, J. C. Kappes et al., 2003. Antibody neutralization and escape by HIV-1. Nature 422: 307–312. [DOI] [PubMed] [Google Scholar]
  63. Williamson, S., 2003. Adaptation in the env gene of HIV-1 and evolutionary theories of disease progression. Mol. Biol. Evol. 20: 1318–1325. [DOI] [PubMed] [Google Scholar]
  64. Williamson, S., and M. E. Orive, 2002. The genealogy of a sequence subject to purifying selection at multiple sites. Mol. Biol. Evol. 19: 1376–1384. [DOI] [PubMed] [Google Scholar]
  65. Wilson, D. J., and G. McVean, 2006. Estimating diversifying selection and functional constraint in the presence of recombination. Genetics 172: 1411–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Wolfs, T. F., J. J. de Jong, H. Van den Berg, J. M. Tijnagel, W. J. Krone et al., 1990. Evolution of sequences encoding the principal neutralization epitope of human immunodeficiency virus 1 is host dependent, rapid, and continuous. Proc. Natl. Acad. Sci. USA 87: 9938–9942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Wright, S., 1931. Evolution in Mendelian populations. Genetics 16: 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Wyatt, R., and J. Sodroski, 1998. The HIV-1 envelope glycoproteins: fusogens, antigens, and immunogens. Science 280: 1884–1888. [DOI] [PubMed] [Google Scholar]
  69. Yang, Z., 1994. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 39: 306–314. [DOI] [PubMed] [Google Scholar]
  70. Zhuang, J., A. E. Jetzt, G. Sun, H. Yu, G. Klarmann et al., 2002. Human immunodeficiency virus type 1 recombination: rate, fidelity, and putative hot spots. J. Virol. 76: 11273–11282. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES