Abstract
The change in the membrane potential of Jurkat cells in response to nanosecond pulsed electric fields was studied for pulses with a duration of 60 ns and maximum field strengths of ∼100 kV/cm (100 V/cell diameter). Membranes of Jurkat cells were stained with a fast voltage-sensitive dye, ANNINE-6, which has a subnanosecond voltage response time. A temporal resolution of 5 ns was achieved by the excitation of this dye with a tunable laser pulse. The laser pulse was synchronized with the applied electric field to record images at times before, during, and after exposure. When exposing the Jurkat cells to a pulse, the voltage across the membrane at the anodic pole of the cell reached values of 1.6 V after 15 ns, almost twice the voltage level generally required for electroporation. Voltages across the membrane on the side facing the cathode reached values of only 0.6 V in the same time period, indicating a strong asymmetry in conduction mechanisms in the membranes of the two opposite cell hemispheres. This small voltage drop of 0.6–1.6 V across the plasma membrane demonstrates that nearly the entire imposed electric field of 10 V/μm penetrates into the interior of the cell and every organelle.
INTRODUCTION
When mammalian cells are placed in a static or slowly varying electric field, charges will accumulate along the plasma membrane and, as a result, the potential difference across the membrane will change from the resting value. The plasma membrane behaves as a leaky dielectric, and when the voltage is increased to ∼1 V, water-filled pores form in the lipid bilayer resulting in “electroporation” (1,2). This leads to an increased permeability of the cell membrane (3), allowing for transfer of molecules across the cell membrane. The pore size is a function of the duration of the electric field pulse. Traditional electroporation utilizes pulses microseconds to milliseconds in duration and a few hundred volts to several kilovolts per centimeter. This generates pores large enough for molecules such as DNA to pass through. Current applications of this technique include transfer of genes and drug delivery into cells (4–7). Shorter pulse durations in the nanosecond range are thought to create much smaller pores that will allow ions but not large molecules to pass through (8,9). At higher electric fields, the probability of creating nonresealable pores increases and, for such pores, cells lose their cytoplasm and die. This effect can be used for food processing (10) or bacterial decontamination (11).
If the rise time of the applied pulsed electric field is faster than the charging time of the plasma membrane, the electric field will pass through the membrane into the cytoplasm and affect internal cell structures. If the amplitude of the applied field is high enough, transmembrane voltages across intracellular membranes will reach threshold values, and pore formation in such membranes becomes likely (12). Although the charging mechanism for intracellular membranes is not yet completely understood, the use of ultrashort pulses on such membranes has been shown to cause a number of new biochemical and biological phenomena. Among the events observed so far are the transient externalization of phosphatidyl serine (13), the release of intracellular calcium (14,15), and the induction of apoptosis (16,17).
Better understanding of the effects of pulsed electric fields on membranes requires the measurement of transmembrane voltages in real time, i.e., with a temporal resolution short compared to the charging time of the membrane. Because characteristic charging time constants for the plasma membrane of mammalian cells are on the order of 100 ns, and even less for membranes of subcellular structures (18), real-time measurements require a temporal resolution of 1–10 ns. For larger cells, e.g., sea urchin eggs, where the characteristic membrane charging time constant is in the microsecond range, real-time measurements of membrane charging only require a temporal resolution on the order of 100 ns. Such measurements have been conducted by Kinosita et al. (19) for applied square wave pulses of several microseconds duration and a maximum field strength of 400 V/cm by using a 300-ns laser pulse to excite the voltage sensitive dye, RH292. The advantage of this pulsed illumination with the laser is that the temporal resolution of the measurement is not determined by the shutter time of the camera but by the pulsed (stroboscopic) laser illumination only. The results of the experiments with 400 V/cm pulses showed an exponential increase in the transmembrane voltage until saturation was reached after 2 μs. The saturation of the fluorescence response was assumed to be due to electroporation.
To use the same technique to monitor the transmembrane potential during the exposure to a nanosecond pulsed electric field, a laser pulse of nanosecond pulse duration and a voltage sensitive dye with an equally fast response time are needed. Whereas nanosecond lasers are readily available, only recently has a voltage-sensitive dye, ANNINE-6, with subnanosecond temporal response, become available. ANNINE-6 was developed with a voltage-regulated fluorescence response that depends only on the shift of energy levels due to the Stark effect (20).
To investigate membrane charging in response to an ultrashort pulsed electric field, we stained Jurkat cells with Annine-6 and exposed them to an electric field of 95 kV/cm for 60 ns. At different times during the exposure, the cells were illuminated with a laser pulse of 5-ns duration (fullwidth half-maximum (FWHM)). In this manner, the recorded changes in fluorescence intensity allowed us to monitor temporal development of the transmembrane voltage with a 5-ns temporal resolution.
MATERIALS AND METHODS
Cell culture
Jurkat cells, a T-lymphocyte cell line obtained from American Type Culture Collection (Manassas, VA), were cultured in 75-cm2 flasks in phenol red RPMI 1640 medium (Mediatech Cellgro, Herndon, VA) supplemented with 10% fetal bovine serum (Atlanta Biologicals, Norcross, GA), 1% L-glutamine, and 1% penicillin/streptomycin (Mediatech Cellgro), and incubated at 37°C with 5% CO2. Cells in log-phase were removed from the culture and resuspended in a physiological buffer before experimentation. The buffer used to resuspend the Jurkat cells was composed of 145 mM NaCl, 5 mM KCl, 0.4 mM NaH2PO4, 1 mM MgSO4, 6 mM glucose, 5 mM HEPES, 1.5 mM CaCl2, with enough NaOH added to bring the pH to 7.4.
Cell staining
Cells were stained with the voltage-sensitive fast response dye ANNINE-6 (Sensitive Dyes GbR, Munich Germany) at a concentration of 16 μM (20). The dye molecules become attached to the cellular membrane, and undergo a change in charge distribution when the voltage across the membrane, or the electric field in the membrane, respectively, is increased. This increase in electric field, causes a change in charge distribution of the molecule. This field-induced redistribution occurs on a timescale small compared to nanoseconds, and leads to a shift of the excitation and emission spectra of ANNINE-6. Kuhn and co-workers (21) found strong experimental evidence that the spectral shifts of ANNINE-6 embedded in a plasma membrane depend on the molecular Stark effect (electrochromism) only (22). As a result of the spectral shift, the fluorescence intensity of ANNINE-6 that is observed in a certain wavelength range is modulated strongly by the voltage across the membrane (21) with a response time of ANNINE-6 in the subnanosecond range.
Experimental setup
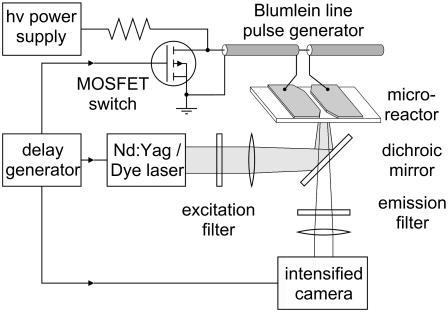
Stained cells in suspension were placed between two stainless steel electrodes (type 301, Small Parts, Miami Lakes, FL) mounted on a standard (25 × 75 mm) microscope slide. Although some authors doubt the chemical inertness of stainless steel electrodes in experiments with electric fields (23,24), we have found no adverse effects caused by the material in our experiments thus far. The gap distance between the electrodes is 100 μm (depth and length of the gap are 100 μm and 1 cm, respectively) and the electrodes are affixed to the slide with a <10-μm epoxy layer. A homogeneous electric field was applied to the suspension by means of a Blumlein line pulse generator matched to the load resistance of the sample between the electrodes (25). The pulse duration is determined by the cable length of the Blumlein line and was set to 60 ns for this experiment. To synchronize the exposure with the pulsed illumination, a fast semiconductor switch (MOSFET (DE275-102N06A, IXYS RF, Fort Collins, CO)) was used as a closing switch for the Blumlein line pulse generator. The MOSFET, which can be triggered with a TTL signal, allows the application of a voltage pulse with amplitude up to 1 kV, corresponding to a maximum electric field in the 100-μm gap of 95 kV/cm. A schematic of the experimental setup is shown in Fig. 1.
FIGURE 1.
Block diagram of the experimental setup: nanosecond pulse generator, microreactor, and optical system.
The required nanosecond pulsed illumination was accomplished with a dye laser (PDL-2, Quanta Ray, Spectra Physics, Mountain View, CA). The dye laser was pumped by the third harmonic of an Nd:Yag laser (DCR-3, Quanta Ray). Coumarin 440 (Exciton, Dayton, OH) was used in the dye laser to provide illumination at a wavelength close to the excitation maximum of Annine-6 at 440 nm. The pulse duration of the multimode laser pulse was 5 ns (FWHM). The laser light is guided through an optical fiber to the microscope, where it is weakly focused on the area between the electrodes of the microreactor on the microscope stage. The diameter of the illuminated spot in the specimen plane is 180 μm. To ensure reproducibility, the laser intensity was adjusted to the same value in each experiment. A filter with an optical transmission peaking at 440 nm and a FWHM of 20 nm prevents excitation of the sample by the laser used to pump the dye laser itself (355, 532, and 1064 nm) and by stray light from sources other than the laser. To further minimize the influence of stray light, the fluorescence emission is observed through a combination of a dichroic mirror and a bandpass filter with a range from 560 to 660 nm. The transmission of this filter is 88 ± 2% over the entire range.
The peak laser power density at the illuminated area A = 2.54 × 10−4 cm2, amounts to 5 MW/cm2. Thus, the peak photon flux density at the specimen plane is Ipeak = 1.1 × 1025 photons per cm2 and per second. Dye excitation at these moderate power densities is a single-photon process. For two-photon excitation of common fluorescent probes, a photon flux density on the order of 1030 cm−2s−1 is typically required (26), which is five orders of magnitude higher than is used in the experiment.
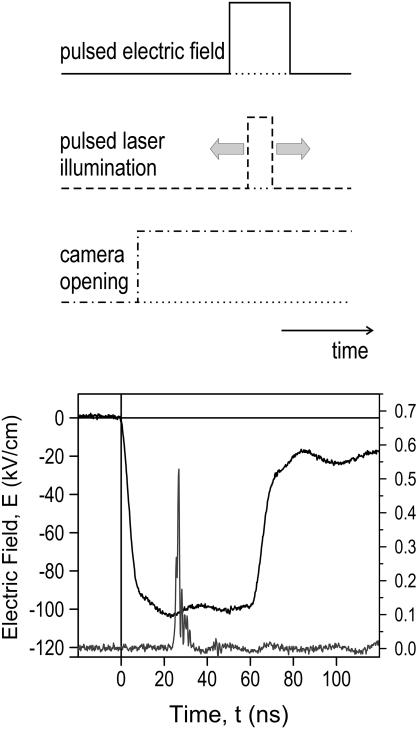
The laser was operated in single-shot mode triggered by an external signal that was synchronized with the electric field pulse. The timing was controlled with a fast photodiode (S4797, Hamamatsu; Hamamatsu City, Japan). All propagation delays were accounted for and corrected by using appropriate delays on the trigger signals. The principle of the stroboscopic imaging technique is shown in Fig. 2. The voltage pulse applied to the microreactor was trapezoidal with a rise and fall time of ∼5 ns (10–90% value). The pulse voltage did not return to zero after 60 ns, but stayed, for another 60 ns, at ∼20% of its peak value.
FIGURE 2.
The concept of stroboscopic measurements is depicted on the left. The actual laser pulse of 5 ns (recorded with a fast photodiode), relative to the temporal development of the 60-ns applied electric field is shown in the right graphic.
With this system, it is possible to collect images with a temporal resolution of 5 ns, the duration of the laser pulse, by illuminating the cells at different times before, during, and after the 60-ns electrical exposure. It needs to be pointed out, however, that the setup allows the capture of only one image during each exposure to a pulsed electric field. Therefore, the development of the transmembrane voltage is necessarily a reconstruction from repeated experiments with different cell samples recorded at different times during the electric field exposure.
Fluorescence microscopy
Photographs of the cell sample were taken on an inverted microscope (IX71, Olympus, Melville, NY) with a 600× magnification. A photograph was taken as a reference before the electric field exposure, another during the application of the electric field, and one 30 s after the pulse. The images of the cells were recorded in 12-bit grayscale with a signal amplifying camera (PCO DiCAM Pro, The Cooke Corporation, Auburn Hills, MI). Image processing was done using ImageJ software (National Institutes of Health, rsb.info.nih.gov/ij/). In each image, two to 10 cells were visible between the electrodes. From these cells, a maximum of five cells were analyzed. A circular mask was drawn around each selected cell in the control image taken before exposure to the electrical field, and its dimensions recorded. A smaller circular mask was then drawn to 25% the size of the original and placed at the outermost position (pole) of the membrane facing the cathode and that facing the anode. The average pixel intensity for the selected mask area at both positions was then measured. The same process was repeated for the image taken during the electric field pulse. Background values for each image were subtracted from average pixel intensity values. Once these values were obtained, a ratio of the average fluorescence intensity change in the images, taken before and during the electrical exposure was calculated and expressed as a percentage change in fluorescence intensity. Changes in the fluorescence intensity could be determined with an accuracy of 2%. However, the fluorescence intensity of cells observed in successive experiments with the same exposure parameters varied as much as 12%.
The Jurkat cells were stained with a voltage-sensitive dye, ANNINE-6, having a subnanosecond temporal response (21). With a high-intensity laser as excitation source, almost all the dye molecules that are embedded in the membrane will be excited. Because the lifetime of the excited state is on the same order as the laser pulse duration, 5 ns, multiple excitation cycles of the dye molecules are not likely (in contrast to the static illumination by a mercury lamp, where continuous excitation and fluorescent decay occurs). Consequently, for the pulsed laser illumination, the fluorescence signal depends on the number of dye molecules attached to the membrane, rather than on the intensity of the incident light.
A laser intensity that is too high results in rapid bleaching of the dye, rendering measurements on transmembrane potential changes futile. To take the influence of laser bleaching into account, we have adjusted the laser intensity to a value that gave us a reproducible fluorescent signal reduction of 80% after 10 laser pulses. In addition, a control image was always taken as the third picture in a sequence of pictures before, during, and after the exposure to the pulsed electric field. The comparison of the fluorescence intensity before and after the application of the electrical pulse, together with the information from images recorded in the same sequence but without the effect of an applied electrical pulse, allows us to estimate “inherent” changes in fluorescent intensity that are not caused by changes in the transmembrane voltage. Small fluctuations in the intensity of the laser illumination are responsible for changes in fluorescence of 5–10% between the first and the second image. For a nominal laser energy of 5 μJ (corresponding to a power density of 5 MW/cm2 at the illuminated focal area), this value was found to be reproducible and was taken into account when the experimental results were evaluated.
Image analysis
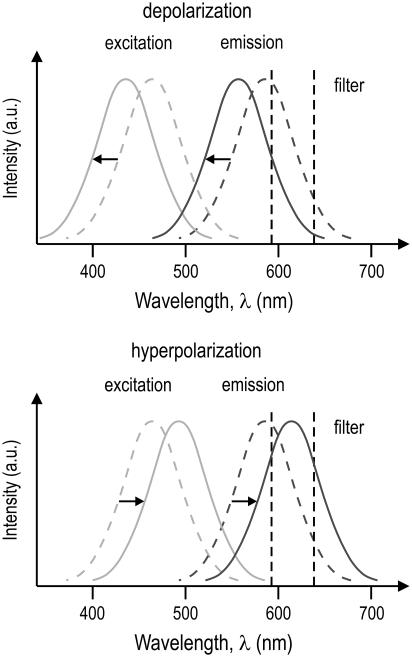
When the voltage across the membrane changes due to the applied electric field, the wavelengths for the excitation and emission maxima shift in response (Fig. 3). When the fluorescence signal is observed through an emission filter with a transmission range small compared to the width of the fluorescence emission band, this shift causes a change in the intensity of the recorded signal. With the data provided by Kuhn et al. (27), transmembrane voltages can be calculated from the change in fluorescence intensity as shown in Fig. 4. For an increase of the electric field across the membrane (hyperpolarization), the fluorescence spectrum shifts toward longer wavelengths, corresponding first to an increase in recorded intensity (up to the point where the peak of the fluorescence spectrum coincides with the center wavelength of the filter transmission), followed by a decrease. The opposite is the case when the electrical field across the membrane decreases (depolarization). The changes in intensity, therefore, provide a measure of the transmembrane voltage.
FIGURE 3.
Excitation and emission spectra of ANNINE-6 are depicted for a resting transmembrane voltage of 50 mV (dashed curves). With decreasing voltage across the membrane (depolarization), the spectra are shifted to shorter wavelengths (solid curves; diagram on left), resulting in a decrease of the light intensity passing through a filter centered at 610 nm with a bandwidth of 100 nm. With increasing transmembrane voltage (hyperpolarization), the spectra are shifted to longer wavelengths (solid curves; diagram on right), resulting in first, an increase, and, with increasing voltage, a decrease in intensity passing through the filter.
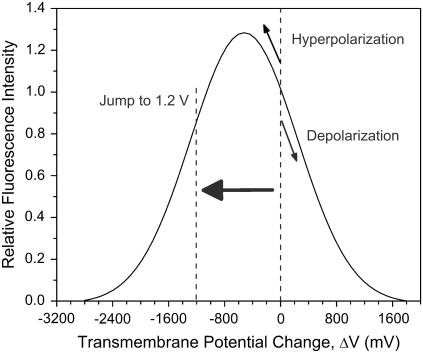
FIGURE 4.
The relative fluorescence intensity of ANNINE-6 versus transmembrane voltage change. The fluorescence has been recorded through a filter centered at 610 nm with a bandwidth of 100 nm and has been normalized with respect to the intensity without electric field application. For a change of the transmembrane voltage at the pole of the cell facing the anode of >1 V the hyperpolarization of the membrane will also lead to a decrease of the fluorescence signal.
RESULTS
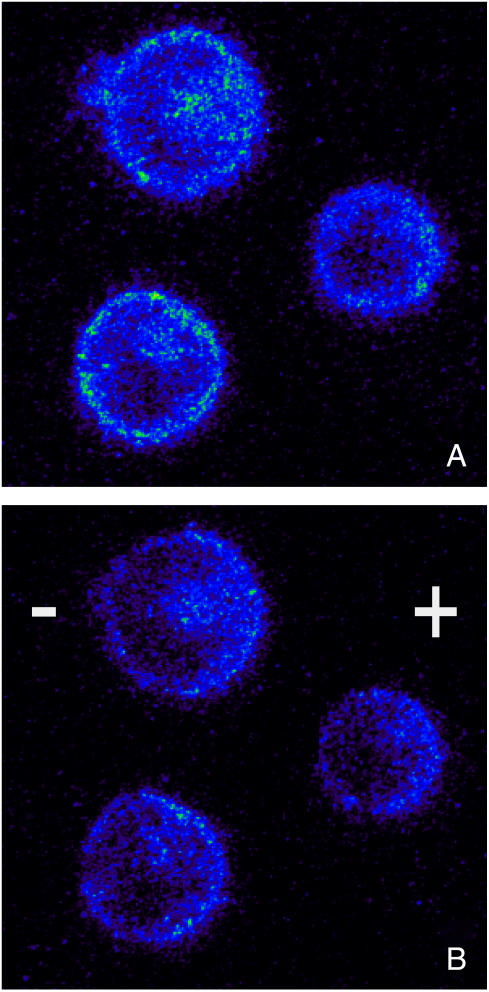
We have imaged Jurkat cells stained with ANNINE-6 before, during, and after the application of a 60-ns pulse of 95 kV/cm. Images were acquired during the excitation of the dye with a 5-ns laser pulse to achieve a snapshot of the membrane voltage of the entire cell with a 5-ns temporal resolution (Fig. 5). Images acquired before the pulse was applied show a fluorescence distribution that is uniform along the perimeter of the cell, as expected for cells where the voltage across the membrane is just the resting potential difference. For Jurkat cells this is ∼50 mV (of negative polarity with respect to the grounded exterior of the cell) (28). When the cells are exposed to high electric fields, the fluorescence decreases dramatically in both hemispheres, slightly more on the hemisphere that faces the cathode (negatively biased electrode) than the hemisphere that faces the anode.
FIGURE 5.
Jurkat cells before (A) and 25 ns into (B) an electric field application. The images show a drastic decrease of the fluorescence intensity during the pulsed electric field, which indicates high membrane voltages. During the pulse, the intensities are different for the anode- and the cathode-directed hemispheres, but within the hemispheres, are independent of the azimuthal angle θ.
Note that no azimuthal differences in fluorescence intensity can be observed within the same hemisphere of the cell for any time during the exposure. The fluorescence intensity shows only a discontinuity at the equator (perpendicular to the electric field). This indicates that for such high electric fields, the membrane voltage “breaks down” very rapidly, and assumes across each hemispherical membrane a constant value, which is independent of the azimuth angle, and which is different from computed voltage distribution, where the membrane is considered an ideal dielectric material:
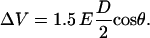 |
(1) |
D is the cell diameter and θ is the angle with respect to the direction of the applied electric field, E. Similar observations have been made by Kinosita et al. for “conventional” electroporation pulses (19).
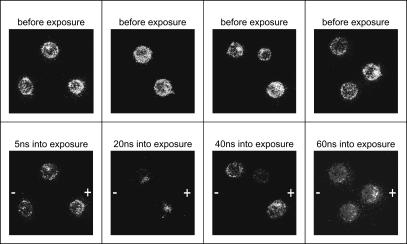
The temporal development of the membrane voltage can be recorded by varying the time of illumination with the laser pulse with respect to the applied electric field pulse. For each experiment we acquired a fluorescence image before the pulse, a second image at a single time point during electric field application, and a third image about half a minute after the pulse. Each measurement sequence was performed on a fresh batch of cells that had not been previously exposed to an electric field. A representative set of images is shown in Fig. 6. We then evaluated at least five such images, taken at the same time point, from five different cells to determine the average change of the fluorescence signal.
FIGURE 6.
Typical images of the fluorescence intensity taken at different times during the exposure. The external electric field was orientated from the right to the left. Cells were exposed to a 60-ns duration pulse of 95-kV/cm electric field and the images were taken at the times listed. Images taken before the pulse (top row) serve as control images.
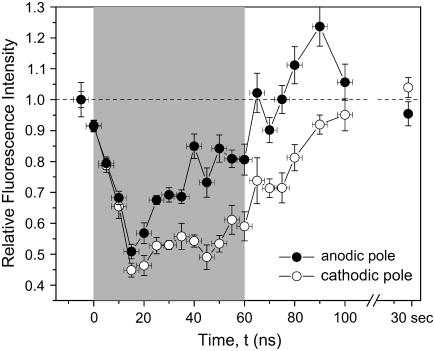
The change in relative fluorescence intensities at the pole of the cell that faces the cathode (negatively biased electrode), and that which faces the anode (positively biased electrode) are plotted versus time in Fig. 7. The gray area depicts the time when the full voltage is applied. The fluorescence intensity rapidly decreases for both the cathodic pole as well as anodic pole, and reaches a minimum ∼15 ns after application of the external field. It then increases slightly at the cathodic pole, and more strongly at the anodic pole, during the application of the 60-ns pulse. After the pulse, the intensity increases at an even faster rate than during the 60-ns pulse, and at 30 s, has almost returned to the value of the unperturbed membrane.
FIGURE 7.
Change of the fluorescence signal in response to a change in transmembrane voltage with time. The data represent the mean fluorescence intensity changes ± SE in three to five experiments. The shaded area depicts the time when the electric field was applied. The change in fluorescence intensity is reaching a maximum at ∼15 ns after the electric field is applied.
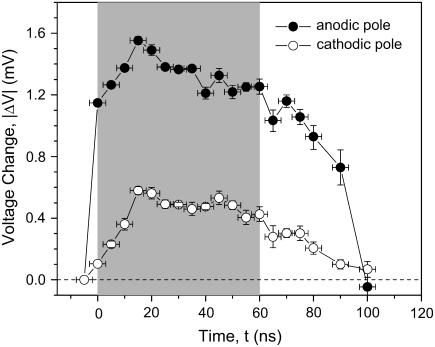
Depolarization is expected for the cathode-facing pole of the cell and hyperpolarization for the pole facing the anode. To correlate the observed fluorescence changes with membrane potential we used the bell-shaped calibration curve shown in Fig. 4. The temporal development of the voltage at the anodic and cathodic side of the cells was calculated accordingly as shown in Fig. 8.
FIGURE 8.
Temporal development of the membrane voltage at the cathodic and anodic pole. The data represent the mean membrane voltages ± SE in three to five experiments. The shaded area depicts the time when the electric field was applied.
We want to point out that the transmembrane voltages, obtained from the fluorescence data, are extrapolated from the available data on the fluorescence response of ANNINE-6, and this extrapolation could be a cause of deviations of the calculated membrane voltage from the real one. Eventually, an experimental calibration of the dye response will be necessary. The design of such measurements for voltages in excess of 1 V is challenging, because independent methods to quantify the membrane potential, such as patch-clamp, require applying very high voltages across the cell for at least several microseconds. Under these conditions, however, the formation of large pores, i.e., “conventional” electroporation of the membrane, is inevitable.
The voltage across the membrane at the anodic pole rises in <5 ns (the temporal resolution of our method) to values of 1.2 V, and then increases at a slower rate of 30 mV/ns to values of 1.6 V, 15 ns after pulse application. During the same time period, the voltage across the membrane at the cathodic pole rises with a rate of ∼40 mV/ns to a value of 0.6 V. From 15 ns forward, up to the end of the 60-ns high voltage pulse, the membrane voltages decrease slightly. After the electrical pulse, the voltages at both hemispheres return to the resting voltage.
DISCUSSION
For ANNINE-6, experimental data on the spectral shift of excitation and emission spectra with voltage are available for transmembrane voltage changes up to ±300 mV, although for a different cell line (27). The shift in wave number was found to be 163 cm−1 for excitation and 170 cm−1 for emission for a change in voltage of 100 mV independent of polarity. We have used these data to calculate the expected response for an excitation wavelength of 440 nm and a range of emission from 560 to 660 nm. The response of the camera in this wavelength range is almost linear as long as the number of counts per pixel is kept on the order of 1000. Consequently a deconvolution with the camera sensitivity curve has a negligible effect on the calibration of voltage change against fluorescence. We can assume that the spectral shift per 100 mV stays the same for voltages in excess of ±300 mV because the fluorescence response caused by the underlying linear Stark effect is not limited to lower voltages. Only for electric fields of >30 MV/cm, do higher order contributions of the field strength become significant in their effect on the shift of electronic energy levels (29). The calculations result in a bell-shaped calibration curve (Fig. 4) where the fluorescence intensity was normalized to one for the undisturbed membrane (ΔV = 0).
The observed decrease of fluorescence of the cathode-facing side is consistent with the predicted change for depolarization (Fig. 4). The fluorescence intensity is expected to decrease continuously with voltage. For the anode-facing pole, one would expect that at the beginning of the pulse, the fluorescence would increase up to 600 mV, the membrane voltage that corresponds to the peak in the calibration curve (Fig. 4) before decreasing again. However, for the 60-ns, 95-kV/cm electrical exposure, an increase in fluorescence intensity was observed only after the end of the 60-ns electric field pulse. This is at a time when the applied electric field has already declined to a value of ∼20 kV/cm. For every other time during the electric field exposure, both hemispheres of the cells show a decrease in fluorescence intensity. For the hemisphere facing the cathode, values as low as 45% are measured ∼15 ns after the onset of the pulsed electric field. The value for the hemisphere on the anode side decreases, at the same time, by ∼50%.
That the expected increase in fluorescence at the anode side during charging was not observed can be explained by the extremely fast rise in membrane voltage, which occurs on a timescale of <5 ns, the resolution of the diagnostic system. Considering that, with a 95-kV/cm electric field applied, the voltage across a 16-μm-diameter cell (the average size of cells in our experiments) reaches 160 V, and that the charging time constant for such a cell embedded in a medium with a conductivity of 1 S/m, and cytosol conductivity of the same value, is on the order of 120 ns, the membrane potential is expected to reach values of 1.2 V (level of fluorescence intensity equal to that with no electric field applied) in ∼1 ns, assuming that there are no changes in the electrical properties of the membrane during this time. With a 5-ns optical exposure time, we would not observe the corresponding initial increase in fluorescence.
After the initial rise in voltage at the anodic pole, the cell membrane becomes permeable (as indicated by the change in the rate of voltage increase), but probably only for small, monovalent or divalent ions. Larger molecules such as propidium iodide were not found to enter the cell when 10-ns pulses of about the same amplitude (80 kV/cm) as our 60-ns pulses were applied to HL-60 cells (8). A possible explanation might be that during the first 15 ns the electric field creates a multitude of small nanopores across the cell membrane previously referred to as “supra-electroporation” (30). The small pore size, coupled with the formation of a screened double layer (an effective depletion zone around the pore periphery) limits the membrane conductivity and ionic throughput. Previous molecular dynamic simulations by our group (9) have demonstrated that nanopore formation can occur within the first 10 ns at these electric field strengths, and validates their nanoscale size.
The lower transmembrane voltage at the cathodic pole in Fig. 8 suggests that the corresponding conduction current must be larger at this end, implying a polarity-dependent asymmetry in electrical transport. There is theoretical (31) and experimental evidence (32) that the anode and cathode sides of cell membranes react very differently to the application of an electric field. Asymmetric pore formation in cell membranes was first reported for plant mesophyll protoplasts by Mehrle et al. (33) who attributed this phenomenon to a superposition of the induced and the resting potentials. It has also been observed for several mammalian cell lines (32,34) and for vesicles (35). Using microsecond, monopolar pulses, transport of various fluorescent markers across anode- and cathode-facing membranes implied a higher density of small pores at the anode side than at the cathode side. Assuming a similar asymmetry for nanosecond pulses, the differences in pore density and size on anode- and cathode-facing membrane must affect the membrane voltage at constant current. It is therefore reasonable to assume that the relatively low voltage across the cathode-facing membrane, which we obtain from our measurements, is due to a strong asymmetry of the ionic transport parameters.
Such an asymmetry in conduction mechanisms at the two opposite poles could be due to formation of cylindrical nanopores with nonuniform cross section. Such pores produce an asymmetric potential profile within the pore region as discussed recently in articles by Siwy et al. (36,37). This asymmetric potential then leads to nonlinear current-voltage characteristics resembling an electrical diode. The role of asymmetric potentials in facilitating and modifying electrical transport is not new, and had been discussed by Astumian in the context of molecular Brownian ratchets (38).
Field-driven translocation of phospholipids might also contribute to an asymmetric potential distribution at opposite hemispheres. Depending on their charge, membrane-embedded molecules will either be driven into the cell or pulled out into the outer leaflet of the membrane. Recent experiments (13) suggest the translocation of phosphatidyl serine during the application of one pulse of >30 kV/cm and duration of 30 ns. As a result of a significant change in membrane surface, charges inside and outside the cell will affect the transmembrane voltage. The expected azimuthal effect on the transmembrane voltage change was not observed in our experiments. Simplified calculations show that the movement of heavy phospholipids through the membrane in large numbers for an applied electric field for pulse durations of <100 ns cannot be explained by the assumption of an electric force acting on the molecules against the friction in the lipid bilayer alone. This was also demonstrated by recent molecular dynamics studies (39) showing that phosphatidyl serine externalization is a pore-mediated event rather than a direct migration through the membrane. The observed asymmetry in transmembrane potential voltages can be explained by an extended screening layer caused by an increase in phosphatidyl serine molecules around the pore on the anode side. Moreover, the simulations demonstrate that the pulse initiates a pore dynamic that will eventually lead to the formation of pores long after (as compared to the pulse duration) the exposure, which will allow not only small ions to pass, but also larger dye molecules. In fact, the experiments mentioned above (13) and work conducted with longer pulses (40) suggest that, with every pulse, the membrane is altered in a way that facilitates phospholipid translocation. As a consequence, an ongoing increase in translocated molecules can still be observed up to milliseconds, or even minutes, after the exposure. A possible explanation for this alteration might be the uptake of water into the membrane, as, for example, in nanopores.
One could presume that another possible reason for the unexpectedly large difference in the calculated anodic and cathodic pole membrane voltage is the assumption that the Stark effect is purely linear. Theoretical studies predict relevant contributions to the shift of energy levels of the dye molecule from the quadratic Stark effect only for electric fields of >30 MV/cm (29) or at least 10 MV/cm (22). Even, if we assume that the membrane is charged to 2 V, the electric field in a cell membrane with a thickness of 5 nm is still only 4 MV/cm, which is too low to expect significant contributions from the quadratic Stark effect that would affect the fluorescence response of the dye. Unfortunately, a calibration of the dye response for transmembrane voltages of 2 V is difficult, if not impossible, because such voltages cannot be applied long enough to the membrane without the formation of pores.
Another very important conclusion drawn from these results is the fact that during the pulse, almost all the voltage across the cell appears across the interior of the cell after conduction pores through the membrane have formed. The voltage drop across the membranes can almost be neglected during this time. That means that the cell interior sees approximately the same electric field as the entire cell: 95 kV/cm. It is reasonable to assume that these high electric fields charge subcellular membranes in the same way as external electric fields charge the outer membrane, and indeed, this “electroporation effect” on subcellular membranes has been observed (41), and is the focus of a large number of current studies (18).
Acknowledgments
We thank Peter Fromherz (Max-Planck Institute for Biochemistry) and Bernd Kuhn (Max-Planck Institute for Medical Research) for their valuable advice and assistance in discussions regarding the ANNINE-6 dye.
This study was funded by an Air Force Office of Scientific Research, Department of Defense, Multidisciplinary University Research Initiative grant on “Subcellular Response to Narrow Band and Wide Band Radio Frequency Radiation” administered by Old Dominion University, Norfolk, VA.
References
- 1.Hamilton, W. A., and A. J. H. Sale. 1967. Effects of high electric fields on microorganisms. II. Mechanisms of action of the lethal effect. Biochim. Biophys. Acta. 148:789–800. [Google Scholar]
- 2.Neumann, E., S. Kakorin, and K. Toensing. 1999. Fundamentals of electroporative delivery of drugs and genes. Bioelectrochem. Bioenerg. 48:3–16. [DOI] [PubMed] [Google Scholar]
- 3.Weaver, J. C., and Y. A. Chizmadzhev. 1996. Theory of electroporation: a review. Bioelectrochem. Bioenerg. 4:135–160. [Google Scholar]
- 4.Hofmann, G. A., S. B. Dev, G. S. Nanda, and D. Rabussay. 1999. Electroporation therapy of solid tumors. Crit. Rev. Ther. Drug Carrier Syst. 16:523–569. [PubMed] [Google Scholar]
- 5.Widera, G., M. Austin, D. Rabussay, C. Goldbeck, S. W. Barnett, M. C. Chen, L. Leung, G. R. Otten, K. Thudium, M. J. Selby, and J. B. Ulmer. 2000. Increased DNA vaccine delivery and immunogenicity by electroporation in vivo. J. Immunol. 164:4635–4640. [DOI] [PubMed] [Google Scholar]
- 6.Dev, S. B., D. P. Rabussay, G. Widera, and G. A. Hofmann. 2000. Medical applications of electroporation. IEEE Transactions on Plasma Science. 28:206–223. [Google Scholar]
- 7.Lucas, M. L., and R. Heller. 2003. IL-12 gene therapy using an electrically mediated nonviral approach reduces metastatic growth of melanoma. DNA Cell Biol. 22:755–763. [DOI] [PubMed] [Google Scholar]
- 8.Chen, N., K. H. Schoenbach, J. F. Kolb, S. R. James, A. L. Garner, J. Yang, R. P. Joshi, and S. J. Beebe. 2004. Leukemic cell intracellular responses to nanosecond electric fields. Biochem. Biophys. Res. Commun. 317:421–427. [DOI] [PubMed] [Google Scholar]
- 9.Hu, Q., S. Viswanadham, R. P. Joshi, K. H. Schoenbach, S. J. Beebe, and P. F. Blackmore. 2005. Simulations of transient membrane behavior in cells subjected to a high-intensity, ultrashort electric pulse. Phys. Rev. E. Stat. Nonlin. Soft. Matter Phys. 71:031914. [DOI] [PubMed] [Google Scholar]
- 10.Schultheiss, C., H. Bluhm, H.-G. Mayer, M. Kern, T. Michelberger, and G. Witte. 2002. Processing of sugarbeets with pulsed-electric fields. IEEE Transactions on Plasma Science. 30:1547–1551. [Google Scholar]
- 11.Schoenbach, K. H., R. P. Joshi, R. H. Stark, F. C. Dobbs, and S. J. Beebe. 2000. Bacterial decontamination of liquids with pulsed electric fields. IEEE Transactions on Dielectrics and Electrical Insulation. 7:637–645. [Google Scholar]
- 12.Schoenbach, K. H., S. J. Beebe, and E. S. Buescher. 2001. Intracellular effect of ultrashort electrical pulses. Bioelectromagnetics. 22:440–448. [DOI] [PubMed] [Google Scholar]
- 13.Vernier, P. T., Y. H. Sun, L. Marcu, C. M. Craft, and M. A. Gundersen. 2004. Nanosecond pulsed electric fields perturb membrane phospholipids in T lymphoblasts. FEBS Lett. 572:103–108. [DOI] [PubMed] [Google Scholar]
- 14.Buescher, E. S., and K. H. Schoenbach. 2003. Effects of submicrosecond, high intensity pulsed electric fields on living cells-intracellular electromanipulation. IEEE Transactions on Dielectrics and Electrical Insulation. 10:788–794. [Google Scholar]
- 15.White, J. A., P. F. Blackmore, K. H. Schoenbach, and S. J. Beebe. 2004. Stimulation of capacitative calcium entry in HL-60 cells by nanosecond pulsed electric fields. J. Biol. Chem. 279:22964–22972. [DOI] [PubMed] [Google Scholar]
- 16.Beebe, S. J., P. M. Fox, L. J. Rec, K. Somers, R. H. Stark, and K. H. Schoenbach. 2002. Nanosecond pulsed electric field (nsPEF) effects on cells and tissues: apoptosis induction and tumor growth inhibition. IEEE Transactions on Plasma Science. 30:286–292. [Google Scholar]
- 17.Beebe, S. J., P. M. Fox, L. J. Rec, E. L. Willis, and K. H. Schoenbach. 2003. Nanosecond, high-intensity pulsed electric fields induce apoptosis in human cells. FASEB J. 17:1493–1495. [DOI] [PubMed] [Google Scholar]
- 18.Schoenbach, K. H., R. P. Joshi, J. F. Kolb, N. Y. Chen, M. Stacey, P. F. Blackmore, E. S. Buescher, and S. J. Beebe. 2004. Ultrashort electrical pulses open a new gateway into biological cells. Proc. IEEE. 92:1122–1137. [Google Scholar]
- 19.Kinosita, K., Jr., I. Ashikawa, N. Saita, H. Yoshimura, H. Itoh, K. Nagayama, and A. Ikegami. 1988. Electroporation of cell membrane visualized under a pulsed-laser fluorescence microscope. Biophys. J. 53:1015–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hubener, G., A. Lambacher, and P. Fromherz. 2003. Anellated hemicyanine dyes with large symmetrical solvatochromism of absorption and fluorescence. J. Phys. Chem. B. 107:7896–7902. [Google Scholar]
- 21.Kuhn, B., and P. Fromherz. 2003. Anellated hemicyanine dyes in a neuron membrane: molecular Stark effect and optical voltage recording. J. Phys. Chem. B. 107:7903–7913. [Google Scholar]
- 22.Loew, L. M., G. W. Bonneville, and J. Surow. 1978. Charge shift optical probes of membrane-potential: theory. Biochemistry. 17:4065–4071. [DOI] [PubMed] [Google Scholar]
- 23.Loomis-Husselbee, J. W., P. J. Cullen, R. F. Irvine, and A. P. Dawson. 1991. Electroporation can cause artifacts due to solubilization of cations from the electrode plates. Biochem. J. 277:883–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tomov, T., and I. Tsoneva. 2000. Are stainless steel electrodes inert? Biochemistry. 51:207–209. [DOI] [PubMed] [Google Scholar]
- 25.Kolb, J. F., S. Kono, and K. H. Schoenbach. 2005. Nanosecond pulsed electric field generators for the study of subcellular effects. Bioelectromagnetics. 27:172–187. [DOI] [PubMed] [Google Scholar]
- 26.Xu, C., W. Zipfel, J. B. Shear, R. M. Williams, and W. W. Webb. 1996. Multiphoton fluorescence excitation: new spectral windows for biological nonlinear microscopy. Proc. Natl. Acad. Sci. USA. 93:10763–10768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kuhn, B., P. Fromherz, and W. Denk. 2004. High sensitivity of Stark-shift voltage-sensing dyes by one- or two-photon excitation near the red spectral edge. Biophys. J. 87:631–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sarkadi, B., A. Tordai, and G. Gardos. 1990. Membrane depolarization selectively inhibits receptor-operated calcium channels in human T (Jurkat) lymphoblasts. Biochim. Biophys. Acta. 1027:130–140. [DOI] [PubMed] [Google Scholar]
- 29.Fischer, J. K., D. M. von Bruning, and H. Labhart. 1976. Light-modulation by electrochromism. Appl. Opt. 15:2812–2816. [DOI] [PubMed] [Google Scholar]
- 30.Stewart, D. A., T. R. Gowrishankar, and J. C. Weaver. 2004. Transport lattice approach to describing cell electroporation: use of a local asymptotic model. IEEE Transactions on Plasma Science. 30:1696–1708. [Google Scholar]
- 31.Loew, L. M. 1999. Potentiometric membrane dyes and imaging membrane potential in single cells. In Fluorescent and Luminescent Probes for Biological Activity. E. Mason, editor. Academic Press. New York. 210–221.
- 32.Tekle, E., R. D. Astumian, and P. B. Chock. 1990. Electro-permeabilization of cell membranes: effect of the resting membrane potential. Biochem. Biophys. Res. Commun. 172:282–287. [DOI] [PubMed] [Google Scholar]
- 33.Mehrle, W., R. Hampp, and U. Zimmermann. 1989. Electric pulse induced membrane permeabilization. Spatial orientation and kinetics of solute efflux in freely suspended and dielectrophoretically aligned plant mesophyll protoplasts. Biochim. Biophys. Acta. 978:267–275. [DOI] [PubMed] [Google Scholar]
- 34.Tekle, E., R. D. Astumian, and P. B. Chock. 1994. Selective and asymmetric molecular transport across electroporated cell membranes. Proc. Natl. Acad. Sci. USA. 91:11512–11516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tekle, E., R. D. Astumian, W. A. Friauf, and P. B. Chock. 2001. Asymmetric pore distribution and loss of membrane lipid in electroporated DOPC vesicles. Biophys. J. 81:960–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Siwy, Z., and A. Fulinski. 2004. A nanodevice for rectification and pumping ions. Am. J. Phys. 72:567–574. [Google Scholar]
- 37.Siwy, Z., and A. Fulinski. 2002. Fabrication of a synthetic nanopore ion pump. Phys. Rev. Lett. 89:198103–1-198103–4. [DOI] [PubMed] [Google Scholar]
- 38.Astumian, R. D. 1997. Thermodynamics and kinetics of a Brownian motor. Science. 276:917–922. [DOI] [PubMed] [Google Scholar]
- 39.Hu, Q., V. Srindhara, R. P. Joshi, J. F. Kolb, and K. H. Schoenbach. 2006. Molecular dynamics analysis of high electric pulse effects on bilayer membranes containing DPPC and DPPS. IEEE Transactions on Plasma Science. In press.
- 40.Haest, C. W. M., D. Kamp, and B. Deuticke. 1997. Transbilayer reorientation of phospholipid probes in the human erythrocyte membrane. Lessons from studies on electroporated and resealed cells. Biochim. Biophys. Acta. 1325:17–33. [DOI] [PubMed] [Google Scholar]
- 41.Schoenbach, K. H., S. J. Beebe, and E. S. Buescher. 2001. Intracellular effect of ultrashort electrical pulses. Bioelectromagnetics. 22:440–448. [DOI] [PubMed] [Google Scholar]