Abstract
Two mixed bilayers containing dipalmitoylphosphatidylcholine and dipalmitoylphosphatidylserine at a ratio of 5:1 are simulated in NaCl electrolyte solutions of different concentration using the molecular dynamics technique. Direct NH···O and CH···O hydrogen bonding between lipids was observed to serve as the basis of interlipid complexation. It is deduced from our results and previous studies that dipalmitoylphosphatidylcholine alone is less likely to form interlipid complexes than in the presence of bound ions or other bilayer “impurities” such as dipalmitoylphosphatidylserine. The binding of counterions is observed and quantitated. Based upon the calculated ion binding constants, the Gouy-Chapman surface potential (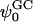 ) is calculated. In addition we calculated the electrostatic potential profile (Φ) by twice integrating the system charge distribution. A large discrepancy between
) is calculated. In addition we calculated the electrostatic potential profile (Φ) by twice integrating the system charge distribution. A large discrepancy between 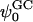 and the value of Φ at the membrane surface is observed. However, at “larger” distance from the bilayer surface, a qualitative similarity in the z-profiles of Φ and ψGC is seen. The discrepancy between the two potential profiles near the bilayer surface is attributed to the discrete and nonbulk-like nature of water in the interfacial region and to the complex geometry of this region.
and the value of Φ at the membrane surface is observed. However, at “larger” distance from the bilayer surface, a qualitative similarity in the z-profiles of Φ and ψGC is seen. The discrepancy between the two potential profiles near the bilayer surface is attributed to the discrete and nonbulk-like nature of water in the interfacial region and to the complex geometry of this region.
INTRODUCTION
The cellular membrane is a self-assembled set of macromolecular components that serves as a barrier and intermediary between two distinct chemical media—the inner and outer cellular contents. The species that compose the majority of the membrane are zwitterionic (such as phosphatidylcholine (PC)) and acidic (such as phosphatidylserine (PS)) lipids. Though these species are in the majority, in reality, biomembranes are quite complex mixtures of not only these simple lipids, but also of proteins and sterols. The interfacial region of membranes in electrolyte solution is a site of complex interactions between water molecules, lipid headgroups, proteins, and ions. In the majority of cases, biological membranes carry negative charge, and the surface charge density on the membrane is on the order of −0.05 C/m2 (Cevc, 1990). The presence of charged surfaces at the interface, due to lipids such as acidic PS lipids, and also the presence of bound ions and highly polarized water molecules that exhibit nonbulk-like properties (Pandit et al., 2003a) give rise to biologically important electrostatic properties. For example, adsorption of some peripheral proteins to the plasma membrane requires the electrostatic interaction of a cluster of basic residues of the protein with acidic lipids in the membrane (McLaughlin and Aderem, 1995).
To begin investigating the way in which these various molecular species interact to perform their function, many studies focus first on model membrane systems—simple single-component or binary mixtures of biomembrane components. Even after making these simplifications, the study of model membranes is still quite daunting. In particular, bilayers containing a mixture of PC and PS molecules present many complications. It is known that such a mixture is nonideal in nature (Huang et al., 1993). Furthermore, in the presence of divalent cations, these mixed bilayers are observed to show a phase separation (Jacobson and Papahadjopoulos, 1975; Luna and McConnell, 1977; Reviakine et al., 2000; van Dijck et al., 1978) that is undoubtedly due to specific lipid-lipid and lipid-ion interactions. Experimental methods possess the ability to observe such macroscopic events as phase separation. On the other hand, the microscopic molecular details of the interactions that give rise to these events might be a suitable goal for computational study. The most utilized computational technique for molecular systems, molecular dynamics (MD) simulation, can give some insight to this issue, though the timescale and length scale for observation of events such as phase separation are not attainable as yet.
In many cases, experimental studies that glean information about the electrostatic properties of the membrane interface make use of electrophoretic methods (Cevc, 1990; Eisenberg et al., 1979; McLaughlin, 1989; Tatulian, 1987). In such experiments, the electrophoretic mobility of vesicles in electrolyte is determined. The ζ-potential is calculated from this mobility using the Helmholtz-Smoluchowski equation. The membrane surface charge density is then determined by calculating the intrinsic binding constant of ions using the Langmuir isotherm along with the Gouy-Chapman (GC) theory.
Ultimately, the results from this experimental method depend upon the validity of the GC theory. This theory is based on the Poisson-Boltzmann equation. The GC theory uses a simple model where a membrane of thickness δ and low dielectric constant ε′ separates two regions containing ionic solutions immersed in water represented as a dielectric continuum with a dielectric constant ε (Cevc, 1990; McLaughlin, 1977, 1989). The GC model assumes that the interface between the membrane and aqueous solution is planar with zero width and that the charge on the membrane is homogeneously distributed on the membrane surface in a continuous way. The ions in the GC description are represented as point charges immersed in a dielectric continuum and the ion-ion correlation is neglected. Most of the theoretical and simulation work done on the extension of the GC model has considered a rather simple interface and has concentrated on understanding the effects due to ion-ion correlation (Carnie and Torrie, 1984; Greberg et al., 1997; Mar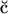 elja, 2000; Boda et al., 1999), the discrete character of water solvent (Boda et al., 1998, 2000), ion size (Crozier et al., 2001), and recently, the effect of surface charge modulations on the electrical properties of the interface (Lukatsky et al., 2002).
elja, 2000; Boda et al., 1999), the discrete character of water solvent (Boda et al., 1998, 2000), ion size (Crozier et al., 2001), and recently, the effect of surface charge modulations on the electrical properties of the interface (Lukatsky et al., 2002).
The assumption that the membrane/aqueous solution interface is planar with zero width has always been considered rather dramatic. One would hope that the powerful technique of computer simulation can help in our understanding of the nature of this interface. Recent simulations mostly performed on neutral phospholipid bilayers convincingly illustrated that the width of the water/membrane interface and structure of the interface cannot be neglected since the interface represents a large portion of the system under consideration (Marrink et al., 1993; Pandit et al., 2003b,a). The issue of electrostatics at the interface of charged membranes, especially in the presence of electrolyte, has not yet been addressed by computer simulation studies.
To fill this gap we present the results from two detailed simulations of a bilayer containing a mixture of dipalmytoylphosphatidylcholine (DPPC) and dipalmitoylphosphatidylserine (DPPS) phospholipids (Fig. 1) immersed in an aqueous solution containing water molecules, 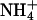 counterions, and NaCl salt.
counterions, and NaCl salt.
FIGURE 1.
Structures of the simulated DPPS (PS) and DPPC (PC) molecules. The atom naming is adopted from a previous convention (Smondyrev and Berkowitz, 1999).
METHODS
MD simulations were performed on two bilayer systems composed of a mixture of 106 DPPC and 22 DPPS molecules (a ∼5:1 mixture of DPPC:DPPS) with 22 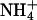 counterions in NaCl electrolyte solution. Although both systems contained 6562 water molecules, one of them contained 22 Na+ and 22 Cl− ions, giving rise to an initial concentration of ∼0.19 M NaCl (referred to as the S1 system), and the other contained 36 Na+ and 36 Cl− ions, giving rise to an initial concentration of ∼0.30 M NaCl (referred to as the S2 system). The DPPC:DPPS ratio was chosen such that the number of counterions in the system could be kept relatively small. This provision allowed us to focus on the alkyl-halide salt's distribution properties, and its interaction with the membrane.
counterions in NaCl electrolyte solution. Although both systems contained 6562 water molecules, one of them contained 22 Na+ and 22 Cl− ions, giving rise to an initial concentration of ∼0.19 M NaCl (referred to as the S1 system), and the other contained 36 Na+ and 36 Cl− ions, giving rise to an initial concentration of ∼0.30 M NaCl (referred to as the S2 system). The DPPC:DPPS ratio was chosen such that the number of counterions in the system could be kept relatively small. This provision allowed us to focus on the alkyl-halide salt's distribution properties, and its interaction with the membrane.
The use of MD simulation in the study of distribution properties of salt (e.g., density and electrostatics) in the aqueous baths surrounding the bilayer deserves mention. Since the computational cost of such studies leads one to study small patches of bilayer, it is essential that the number of ions in the system is chosen carefully. Ideally, the concentration of ions in the system should be as small as possible such that ion-ion correlation is negligible, and comparison with the Gouy-Chapman electrostatic theory of ions near a charged surface might be applicable. On the other hand, the concentration should not be so low as to provide poor statistical sampling of the ion distribution given a tractable simulation time. It was with these thoughts in mind that we chose the initial concentrations of NaCl electrolyte for our simulations to be 0.19 M and 0.3 M. These concentrations provided us with data where ion-ion correlation is relatively small, and also allowed us to observe concentration-dependent differences in the system properties.
The bilayer mixture was prepared by independently creating two monolayers, each containing 53 DPPC and 11 DPPS molecules. The lipids were initially randomly placed on their monolayer planes with their tails in an all-trans conformation. These monolayers were placed to form a bilayer with tails pointing inward and a phosphorus-phosphorus interleaflet distance of 50 Å. The initial random dispersal of lipid molecules is justified in the presence of monovalent ions because clustered domains of DPPS are only observed in experiments for systems containing divalent ions (Jacobson and Papahadjopoulos, 1975; Huang et al., 1993; Luna and McConnell, 1977; Reviakine et al., 2000; van Dijck et al., 1978). Given that DPPS is not expected to be clustered, the fact that it is not possible to observe appreciable lateral motion of the lipids in a relatively short simulation time should not strongly affect the measurement of quantities related to ion binding. Two slabs of NaCl electrolyte solution and 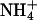 ions were then independently created by randomly placing 3281 SPC water molecules, 11
ions were then independently created by randomly placing 3281 SPC water molecules, 11 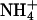 ions, and the appropriate amount of Na+ and Cl− ions for each system on either side of the existing bilayer. With this initial configuration, we proceeded to relax the two systems.
ions, and the appropriate amount of Na+ and Cl− ions for each system on either side of the existing bilayer. With this initial configuration, we proceeded to relax the two systems.
All simulations were performed at the North Carolina Supercomputing Center using the GROMACS package (Berendsen et al., 1995; Lindahl et al., 2001) with a time step of 4 fs. The force field parameters for lipids were based on the work of Berger (Berger et al., 1997). All bonds in the system were constrained using the LINCS algorithm (Hess et al., 1997). Periodic boundary conditions were applied in all three dimensions and long-range electrostatics were handled using the SPME algorithm with a real-space cutoff of 0.9 nm and a tolerance of 10−5 (Essmann et al., 1995). The temperature in all simulations was maintained using the Nose-Hoover scheme with a thermostat relaxation time of 0.5 ps. Analysis of subsequent results was performed using a combination of GROMACS analysis utilities and our own code. Simulations under constant pressure conditions utilized the Parrinello-Rahman pressure coupling scheme (Nose and Klein, 1983; Parrinello and Rahman, 1981) with a barostat relaxation time of 2.0 ps at a pressure of 1 atm.
A series of short simulations for both systems (each of 40 ps duration) was performed in an NVT ensemble at 350 K, keeping the phosphorus atoms frozen to their initial locations. The monolayers were brought closer to each other after each short simulation until the phosphorus-phosphorus distance reached the value of 38 Å. The dimension of the simulation box along the bilayer normal (z-dimension) was then adjusted such that the bulk electrolyte density was close to 1 g/cm3. Since the initial conformation of the lipid tails was all-trans, an additional 100 ps simulation at a temperature of 500 K was performed to ensure their disorder. The temperature was then decreased by performing a set of 100 ps simulations, each at a temperature lowered by 50 K until a final temperature of 350 K was reached. Both systems were then simulated in an NPT ensemble while monitoring the centers of mass of the co- and counterions to ascertain their equilibration. The S1 system was simulated for 15 ns whereas the S2 system was simulated for 20 ns. The trajectory was sampled at an interval of 1 ps for the analysis of each simulation. Since the ions' centers of mass were seen to be stable over the last 5 ns of both trajectories, this portion of each trajectory was used in our analysis. The time-series data for the ions' centers of mass for this portion of both simulations is shown in Fig. 2.
FIGURE 2.
Time series data of the centers of mass of the ions in both systems.
RESULTS AND DISCUSSION
Structural properties
The dimensions of the simulation cell for each calculation were monitored, allowing us to obtain the area per lipid headgroup in both cases. This quantity was 60.1 ± 1.2 Å2 in the S1 system and 58.5 ± 1.0 Å2 in the S2 system. These values compare well with those of pure DPPC bilayers (Pandit et al., 2003b) in 0.1 M NaCl electrolyte solution (∼60.5 Å2) and pure, hydrated DPPC bilayer in the absence of salt (∼62.7 Å2). Though nearly all of these values of the area per headgroup are equivalent considering their uncertainties, there is a distinct trend implying that this quantity decreases upon increasing the salt concentration.
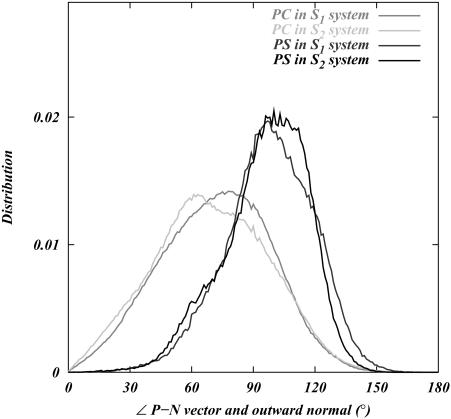
The orientation of lipid headgroups in the presence of the different concentrations of electrolyte was studied by calculating the angle between the phosphorus-nitrogen (P-N) vector, 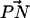 , and the outwardly directed bilayer normal. The distribution of this angle for both systems is shown in Fig. 3. Although there is substantial overlap of the PC and PS orientational distributions, there is a well-resolved difference in their orientational preference. The DPPC
, and the outwardly directed bilayer normal. The distribution of this angle for both systems is shown in Fig. 3. Although there is substantial overlap of the PC and PS orientational distributions, there is a well-resolved difference in their orientational preference. The DPPC 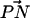 distribution in the S1 system is seen to be nearly the same as in previous studies on pure DPPC bilayer in the absence of salt (Pandit et al., 2003b). This distribution indicates that the DPPC headgroups prefer an orientation that is nearly parallel to the bilayer surface (∼78° ± 21° with respect to the bilayer normal). The DPPS headgroups prefer a slightly more inwardly directed P-N vector (∼100° ± 17°). DPPS prefers this more inwardly directed conformation most likely because its negatively charged serine carboxyl group likes to “stick out” of the membrane, forcing the nitrogen to take a position closer to the center of the bilayer than the phosphorus. Also, the −NH3 of PS is much less bulky than the −N(CH3)3 of PC, providing less steric hindrance for this moiety to reside closer to the bilayer. Although the distributions are very similar for both systems, the S2 system shows a larger difference in the orientational preference of the headgroups. With this higher ionic concentration, DPPC prefers a slightly more outwardly directed P-N vector, whereas DPPS prefers a slightly more inwardly directed orientation.
distribution in the S1 system is seen to be nearly the same as in previous studies on pure DPPC bilayer in the absence of salt (Pandit et al., 2003b). This distribution indicates that the DPPC headgroups prefer an orientation that is nearly parallel to the bilayer surface (∼78° ± 21° with respect to the bilayer normal). The DPPS headgroups prefer a slightly more inwardly directed P-N vector (∼100° ± 17°). DPPS prefers this more inwardly directed conformation most likely because its negatively charged serine carboxyl group likes to “stick out” of the membrane, forcing the nitrogen to take a position closer to the center of the bilayer than the phosphorus. Also, the −NH3 of PS is much less bulky than the −N(CH3)3 of PC, providing less steric hindrance for this moiety to reside closer to the bilayer. Although the distributions are very similar for both systems, the S2 system shows a larger difference in the orientational preference of the headgroups. With this higher ionic concentration, DPPC prefers a slightly more outwardly directed P-N vector, whereas DPPS prefers a slightly more inwardly directed orientation.
FIGURE 3.
Distribution of the angle between 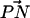 (the vector pointing from the headgroup phosphorus atom to the headgroup nitrogen atom) and the outwardly directed bilayer normal for each lipid in both systems.
(the vector pointing from the headgroup phosphorus atom to the headgroup nitrogen atom) and the outwardly directed bilayer normal for each lipid in both systems.
Lipid complexation through direct hydrogen bonding
This very slight change in orientation seems to be coupled with the complexation of lipids in the system. Phase separation in DPPC:DPPS mixtures have been experimentally observed only in the presence of divalent cations (Jacobson and Papahadjopoulos, 1975; Huang et al., 1993; Luna and McConnell, 1977; Reviakine et al., 2000; van Dijck et al., 1978). Although there are no divalent cations in our simulation, it may be possible to glean what sorts of interactions can occur between lipids in the presence of such cations by observing the interactions in our simulation. The investigation of this possibility would involve a statistical analysis of the frequency of Nlipid-complexes (complexes of lipids involving any single lipid molecule and Nlipid other lipid molecules that are connected to it through direct hydrogen bonding) that occur between DPPC and DPPS in the system. Such an analysis was performed by identifying the ways through which these lipids could form direct intermolecular hydrogen bonds (direct binding modes), and calculating the distribution of these Nlipid-complexes as a function of the number of lipids in each complex.
A DPPS molecule may be a hydrogen bond donor through a moderate NH···O interaction (Jeffrey, 1997). Thus, a geometric criterion was constructed to determine approximately how many lipids were NH···O hydrogen bonded to a single DPPS molecule in our simulation trajectories. An NH···O interaction was identified if the N of a DPPS molecule was seen to be within 0.35 nm of an oxygen atom from a lipid (either DPPC or DPPS) and if the angle between 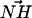 and
and 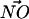 was ≤30° (Jeffrey, 1997). On the other hand, DPPC may form hydrogen bonds with other lipids by donating a hydrogen through a CH···O interaction. Initially, one might be puzzled that such a CH···O interaction might exist. Nonetheless, the idea of the CH···O hydrogen bond is not new and is firmly established (Desiraju, 1991; Gu et al., 1999; Raveendran and Wallen, 2002; Jeffrey, 1997). Though such a hydrogen bond is usually slightly weaker than the typical OH···O hydrogen bond, it is shown that it can be categorized as a true hydrogen bond (Gu et al., 1999). Since the lipid model we use in our simulation does not employ explicit hydrogens on −CH3 groups, the judgment of a CH···O interaction is not straightforward. Thus, we use criteria for identifying such interactions in an approximate way. Typically, the distance between the donor carbon and the acceptor oxygen in the CH···O hydrogen bond is ∼4 Å (Desiraju, 1991; Jeffrey, 1997). We adopted this distance criterion along with the restriction that the angle between the
was ≤30° (Jeffrey, 1997). On the other hand, DPPC may form hydrogen bonds with other lipids by donating a hydrogen through a CH···O interaction. Initially, one might be puzzled that such a CH···O interaction might exist. Nonetheless, the idea of the CH···O hydrogen bond is not new and is firmly established (Desiraju, 1991; Gu et al., 1999; Raveendran and Wallen, 2002; Jeffrey, 1997). Though such a hydrogen bond is usually slightly weaker than the typical OH···O hydrogen bond, it is shown that it can be categorized as a true hydrogen bond (Gu et al., 1999). Since the lipid model we use in our simulation does not employ explicit hydrogens on −CH3 groups, the judgment of a CH···O interaction is not straightforward. Thus, we use criteria for identifying such interactions in an approximate way. Typically, the distance between the donor carbon and the acceptor oxygen in the CH···O hydrogen bond is ∼4 Å (Desiraju, 1991; Jeffrey, 1997). We adopted this distance criterion along with the restriction that the angle between the 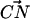 and the
and the 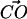 vectors must be in the range between 79° and 139°. This angular restriction makes use of the weak angular dependence of the CH···O hydrogen bond (Desiraju, 1991). It also forces the
vectors must be in the range between 79° and 139°. This angular restriction makes use of the weak angular dependence of the CH···O hydrogen bond (Desiraju, 1991). It also forces the 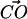 vector to be roughly parallel to the expected
vector to be roughly parallel to the expected 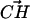 vector in the choline −CH3 groups. The criteria for establishing the DPPS and DPPC hydrogen bonds are summarized in Fig. 4.
vector in the choline −CH3 groups. The criteria for establishing the DPPS and DPPC hydrogen bonds are summarized in Fig. 4.
FIGURE 4.
Schematic diagram showing the established criteria for NH···O and CH···O hydrogen bonding.
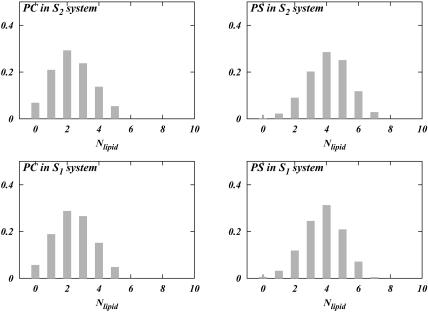
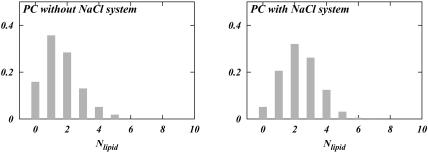
The results of our direct hydrogen bonding analysis are shown in Fig. 5. It is seen that in both S1 and S2 systems, DPPC prefers complexation with two other lipids, whereas DPPS prefers complexation with four. Fig. 5 shows that the distributions for DPPC and DPPS change slightly with the change in the ionic concentration. The distributions show that the number of DPPC complexes with three other lipids is slightly smaller in the S2 system than in the S1 system. On the other hand, complexation with one lipid is more popular in the S2 system than in the S1 system. DPPS seems to behave in a contrary manner. Whereas its preference for five lipids in the S2 system is larger than in the S1 system, its preference for three lipids is smaller in the S2 system. Hence, the changes in headgroup orientation could conceivably be coupled to this change in the hydrogen bonding pattern of the lipids in the mixture. The same sort of analysis was performed for a system containing pure hydrated DPPC bilayer and a pure DPPC bilayer with NaCl electrolyte. The data for these systems were obtained from previous simulations (Pandit et al., 2003b). The result of the analysis in Fig. 6, left, shows that DPPC prefers to be bound to only one other lipid if there is no salt present in the bathing solution. Upon the addition of NaCl, a complexation behavior similar to that of our S1 system emerges (Fig. 6, right). Considering that the area per headgroup in the S1 system and that of our previous simulation of DPPC with NaCl are very similar, we conclude that addition of salt provides DPPC with the ability to change the observed lipid complexation pattern.
FIGURE 5.
Distribution of the number of lipids bound to a given lipid via direct bonding for each PC and PS in both systems.
FIGURE 6.
Distribution of the number of lipids bound to a given lipid via direct bonding in a pure DPPC system with and without salt.
Given that there is a change in the propensity for DPPC complexation with the addition of salt, we further probe what sort of interaction (NH···O or CH···O) the salt enhances in our mixture. The distributions given in Fig. 5 were “coarse-grained” to obtain a gross picture of the propensity of each lipid to form either “larger” or “smaller” complexes. Thus, each distribution was divided at its mean value so that “smaller” DPPC complexes are those involving Nlipid ≤ 2 and “smaller” DPPS complexes are those involving Nlipid ≤ 4. Complexes that are considered “larger” for the two lipid types comprise the complements to the “smaller” complexes in their respective sample spaces (Nlipid > 2 and Nlipid > 4 for DPPC and DPPS, respectively).
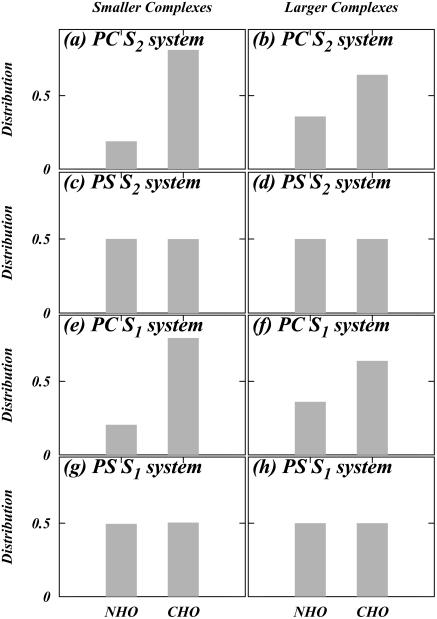
The results of this resampling are summarized in Fig. 7. It is seen that smaller complexes involving DPPC utilize mostly CH···O hydrogen bonds (see Fig. 7, a and e), implying that DPPS does not contribute significantly in the formation of these complexes. However, larger complexes of this species tend to require a relatively larger population of NH···O hydrogen bonds (see Fig. 7, b and f). On the other hand, the size of complexes around DPPS do not exhibit a preference for CH···O or NH···O interactions (Fig. 7, c, d, g, and h). We also observe that the distributions a–d in Fig. 7 for the S2 system are the same as e –h for the S1 system. This indicates that the complexation pattern is unaltered by differences in salt concentration. Fig. 8 shows snapshots of various direct interlipid binding events.
FIGURE 7.
Distribution of different types of direct hydrogen bonding for “smaller” and “larger” lipid complexes for both lipid types in both simulated systems.
FIGURE 8.
Snapshots showing complexation of lipids. A schematic representation of each complex is also shown. In the representations, blue arrows represent PS, black arrows represent PC, and red lines represent the interlipid direct hydrogen bonds. The arrowheads correspond to the nitrogen atom of the headgroup.
These results give rise to a picture of what structural changes must occur within a PC or PS molecule to increase its propensity for complexation. Positively charged ions in the bathing electrolyte attract the negatively charged carboxylate of serine in the DPPS headgroup, forcing its 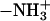 group to be closer to the bilayer. This is why, in the case of DPPS, we observe a consistent comparatively large angle between
group to be closer to the bilayer. This is why, in the case of DPPS, we observe a consistent comparatively large angle between 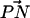 and the outward bilayer normal in Fig. 3. Thus, the DPPS headgroup is placed in a very favorable position to serve as an NH···O hydrogen bond donor to other lipid oxygen atoms. This is the reason that it is able to form larger complexes than DPPC. For example, Fig. 8 c shows the
and the outward bilayer normal in Fig. 3. Thus, the DPPS headgroup is placed in a very favorable position to serve as an NH···O hydrogen bond donor to other lipid oxygen atoms. This is the reason that it is able to form larger complexes than DPPC. For example, Fig. 8 c shows the 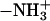 group of a DPPS molecule donating three NH···O hydrogen bonds to neighboring lipids.
group of a DPPS molecule donating three NH···O hydrogen bonds to neighboring lipids.
The story of complexation seems to be more complicated in the case of DPPC. We see that the presence of salt in a pure PC bilayer increases the number of larger complexes (Fig. 6), and that the area per headgroup generally decreases along with an increase in ion concentration. Therefore, the reduction in the area per headgroup caused by ion binding can lead to more complexation of DPPC. Ion binding also has the tendency to make the 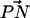 vector of the PC headgroup “stick out” of the bilayer (Fig. 3). This conformational change brings the −CH3 away from other lipids, decreasing the likelihood that the choline group will donate a CH···O hydrogen bond to other lipid oxygens. This explains the observation in the S2 system that the propensity for Nlipid = 3 is smaller whereas that for Nlipid = 1 is larger as compared to the S1 system. A more outwardly directed
vector of the PC headgroup “stick out” of the bilayer (Fig. 3). This conformational change brings the −CH3 away from other lipids, decreasing the likelihood that the choline group will donate a CH···O hydrogen bond to other lipid oxygens. This explains the observation in the S2 system that the propensity for Nlipid = 3 is smaller whereas that for Nlipid = 1 is larger as compared to the S1 system. A more outwardly directed  vector is not conducive to complexation despite the decrease in the area per headgroup. Thus, the activation of DPPC complexation seems to be a delicate balance between the area per headgroup (or closeness of the headgroups) and the
vector is not conducive to complexation despite the decrease in the area per headgroup. Thus, the activation of DPPC complexation seems to be a delicate balance between the area per headgroup (or closeness of the headgroups) and the 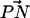 vector orientation.
vector orientation.
Lipid complexation through ion bridging
Apart from complexation via direct hydrogen bonding of lipids to one another, it was found that lipids also form complexes using ions as intermediaries. Such complexation was proposed in a previous work (Pandit et al., 2003b). Here it is investigated in more detail. We constructed ion-lipid bridging criteria to ascertain the number of lipids bound to each ion. We assumed that an 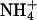 ion participated in a bridging event if a hydrogen bond existed between this ion and a lipid. The criterion for hydrogen bonding between
ion participated in a bridging event if a hydrogen bond existed between this ion and a lipid. The criterion for hydrogen bonding between 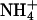 and lipid was adopted from the NH···O hydrogen-bonding criterion described in the previous section. Cl− bridging events were too rare to be sampled in the given interval of time; however, we were able to clearly discern Na+ bridging events. Na+ bonding was said to occur when an acceptor oxygen from DPPC or DPPS came within a distance of 0.32 nm of Na+. This distance was obtained by averaging the radius of the first coordination shell of Na+ with all the oxygen atoms of DPPC and DPPS. An ion was said to form a bridge if and only if it interacted with more than one lipid oxygen. An intermolecular ion bridge is an ion bridge where the interacting oxygens belong to two or more different molecules.
and lipid was adopted from the NH···O hydrogen-bonding criterion described in the previous section. Cl− bridging events were too rare to be sampled in the given interval of time; however, we were able to clearly discern Na+ bridging events. Na+ bonding was said to occur when an acceptor oxygen from DPPC or DPPS came within a distance of 0.32 nm of Na+. This distance was obtained by averaging the radius of the first coordination shell of Na+ with all the oxygen atoms of DPPC and DPPS. An ion was said to form a bridge if and only if it interacted with more than one lipid oxygen. An intermolecular ion bridge is an ion bridge where the interacting oxygens belong to two or more different molecules.
The distribution of the number of lipids with which either Na+ or  forms a bridge is shown for both simulated systems in Fig. 9. The distributions for the S2 system did not change with the reduction of ion concentration in the S1 system. This distribution invariance with respect to ion concentration is consistent with that observed for lipid direct binding. Both Na+ and
forms a bridge is shown for both simulated systems in Fig. 9. The distributions for the S2 system did not change with the reduction of ion concentration in the S1 system. This distribution invariance with respect to ion concentration is consistent with that observed for lipid direct binding. Both Na+ and 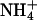 are seen to prefer bridges involving three lipids. Various ion bridging events are shown in Fig. 10.
are seen to prefer bridges involving three lipids. Various ion bridging events are shown in Fig. 10.
FIGURE 9.
Distribution of the number of lipids bound to a single cation for both cation species in both systems.
FIGURE 10.
Snapshots of complexes involving an ion bridge. Na+ (blue sphere) is coordinated with two PC lipids and two PS lipids (left). 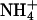 is coordinated with four lipids via hydrogen bonds (right).
is coordinated with four lipids via hydrogen bonds (right).
Ion binding
Given that the ions in our system participate in bridging interactions between lipids, it is interesting to understand how ion binding events may be correlated with such bridging. We have discussed the relation between ion binding and ion hydration in previous work (Pandit et al., 2003b). Our previously established methodology for determining ion binding is used again in this study. We recapitulate certain elements of this methodology here for brevity. In Figs. 11 a and 12 a, we show the dehydration of each ionic species as a function of the distance from the center of the bilayer (z). The hydration of the Na+ and Cl− was taken as the number of water molecules in their first coordination shell. Since the hydration shell of 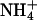 contains NH···O hydrogen bonded water molecules (Jorgensen and Gao, 1986), we defined the hydration of this ion in a more rigorous way than in the cases of Na+ and Cl−. Thus, the
contains NH···O hydrogen bonded water molecules (Jorgensen and Gao, 1986), we defined the hydration of this ion in a more rigorous way than in the cases of Na+ and Cl−. Thus, the  hydration shell was taken to be the number of water molecules to which it was hydrogen bonded. The same criteria for
hydration shell was taken to be the number of water molecules to which it was hydrogen bonded. The same criteria for  hydrogen bonding with water were used as those described previously for the determination of lipid-water NH···O hydrogen bonding. In both S1 and S2 systems, Na+ and
hydrogen bonding with water were used as those described previously for the determination of lipid-water NH···O hydrogen bonding. In both S1 and S2 systems, Na+ and  are seen to begin losing water at z ≤ 2.4 nm. Half of their water is lost at z ≈ 1.8 nm. The S1 system shows very weak binding of Cl− whereas the S2 system shows none. Figs. 11 b and 12 b show the densities of the ions and various components of the systems. In both cases, the Na+ and
are seen to begin losing water at z ≤ 2.4 nm. Half of their water is lost at z ≈ 1.8 nm. The S1 system shows very weak binding of Cl− whereas the S2 system shows none. Figs. 11 b and 12 b show the densities of the ions and various components of the systems. In both cases, the Na+ and 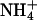 densities overlap with the lipid headgroup phosphorus and nitrogen atoms. However, due to the broad bilayer/electrolyte interface, this overlap alone does not imply binding (Pandit et al., 2003b). The integration of the ion densities provides us with the cumulative number of ions as a function of z (shown in Figs. 11 c and 12 c). Using this information and the criterion that loss of half of an ion's hydration shell implies binding, we can determine the number of ions bound to the membrane surface. These numbers are shown in Table 1.
densities overlap with the lipid headgroup phosphorus and nitrogen atoms. However, due to the broad bilayer/electrolyte interface, this overlap alone does not imply binding (Pandit et al., 2003b). The integration of the ion densities provides us with the cumulative number of ions as a function of z (shown in Figs. 11 c and 12 c). Using this information and the criterion that loss of half of an ion's hydration shell implies binding, we can determine the number of ions bound to the membrane surface. These numbers are shown in Table 1.
FIGURE 11.
Various quantities as a function of z in the S2 system: (a) hydration level of each ion type, (b) densities of various atom types, and (c) number of ions of each type.
FIGURE 12.
Various quantities as a function of z in the S1 system: (a) hydration level of each ion type, (b) densities of various atom types, and (c) number of ions of each type.
TABLE 1.
Data used in the calculation of the binding constant of cations in each system using different binding criteria
| Criterion | System | Ion | Average number of bound ions | Cbulk (M) | α | K (M−1) |
|---|---|---|---|---|---|---|
| Dehydration | S2 | Na+ | 6.0 | 0.199 | 0.0939 | 0.521 |
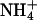 |
3.5 | 0.111 | 0.0547 | 0.520 | ||
| S1 | Na+ | 3.7 | 0.106 | 0.0578 | 0.579 | |
 |
2.8 | 0.105 | 0.0438 | 0.436 | ||
| Bridging | S2 | Na+ | 5.1 | 0.199 | 0.0791 | 0.432 |
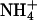 |
4.0 | 0.111 | 0.0620 | 0.487 | ||
| S1 | Na+ | 3.3 | 0.106 | 0.0508 | 0.505 | |
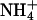 |
4.6 | 0.105 | 0.0716 | 0.734 |
With the number of bound ions in hand, we proceed to calculate their binding constant in a manner consistent with experimental procedures. In doing so, we assume that there exists one binding site per lipid molecule. Thus, we take the fraction of bound ions, α, as the number of bound ions divided by the number of lipids in a single leaflet of the bilayer. The concentration of ions in the bulk is also required to make use of the Langmuir isotherm. These values for the bulk concentrations of ions are summarized in Table 1. The binding constants are obtained using the expression
 |
Usually the value used for the pure PS-Na+ binding constant is ∼1 M−1 (Winiski et al., 1986). The value of the pure PC-Na+ binding constant is ∼0.15 M−1 (Tatulian, 1987). We expect the value of the binding constant for Na+ to our mixed bilayer to be between these values. Thus, the value for the Na+ binding constant calculated here is reasonable. We also note that the value of the Na+ and 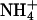 binding constants is not significantly affected by the concentration of ions.
binding constants is not significantly affected by the concentration of ions.
Given that bridging events and binding events are so closely linked, it is interesting to see whether the observation of bridging events for the determination of the binding constant gives consistent results with those using a dehydration criterion. Let us now consider another criterion for discerning whether or not an ion is bound. According to this criterion, an ion is bound to the surface if and only if it is involved in an intra- or intermolecular bridge between lipids. With this new criterion, we again calculated the binding constant following the same steps mentioned above. These results are reported in Table 1 and are consistent with the results obtained using our dehydration criterion.
Electrostatics
Given the wide use of continuum theory in the modeling of electrostatics near membrane surfaces, we thought it might be of interest to determine the surface potential of our membranes using the Gouy-Chapman theory. For this, we calculated the net surface charge using our values for the number of DPPS lipids, the number of ions bound to the membrane surface, and the number of ions in the bulk for each system (see Table 1). The value of the Gouy-Chapman potential was obtained from the following expressions (Israelachvili, 1992):
 |
where the inverse of the Debye length,
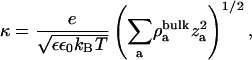 |
σ is the net surface charge density of the membrane including its bound ions, ε is the dielectric constant of water (taken to be 80), 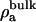 is the number density of the ath ionic species in the bulk, and za is the valence of the ath ionic species. These values are reported in Table 2.
is the number density of the ath ionic species in the bulk, and za is the valence of the ath ionic species. These values are reported in Table 2.
TABLE 2.
Calculated values of surface charge (σ), Debye length (κ−1), and Gouy-Chapman surface potential (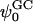 ) based upon the number of bound ions (using different criteria) and ion concentration in the bulk
) based upon the number of bound ions (using different criteria) and ion concentration in the bulk
| Criterion | System | σ (C/m2) | κ−1 (Å) |
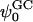 (mV) (mV) |
|---|---|---|---|---|
| Dehydration | S2 | −6.21 × 10−3 | 6.0 | −5.2 |
| S1 | −1.87 × 10−2 | 7.3 | −19.27 | |
| Bridging | S2 | −8.16 × 10−3 | 6.0 | −6.9 |
| S1 | −1.32 × 10−2 | 7.3 | −13.58 |
The value of the ζ-potential reported in electrophoretic mobility experiments on 5:1 DPPC:DPPS mixtures in bulk electrolyte solution of 0.1 M NaCl is ∼−30 mV (McLaughlin, 1989). This is close to the value of ∼−19 mV obtained from our S1 system. Recall that the bulk concentration of NaCl in the S1 system is also ∼0.1 M. (Note that the initial concentration of NaCl, after random distribution, in the S1 system was ∼0.2 M and in the S2 system was ∼0.3 M. After the distribution of ions equilibrates, however, the bulk concentration changes. The final bulk concentration of each system is that shown in Table 1). However, the calculated surface potential values should be considered as indicative rather than exact. Due to the small size of our simulated systems, the calculated surface potential sensitively depends on the number of bound ions. The binding or unbinding of a single ion will drastically affect the calculated surface charge density. Consequently, the Gouy-Chapman surface potential will have a very large uncertainty. Nonetheless, there is a good qualitative agreement between the calculated Gouy-Chapman surface potentials of our simulations and those obtained by electrophoretic mobility experiments.
Since we have performed full, atomistic MD simulations of our mixed bilayer systems with ions, we can make full use of the technique's provisions. Namely, we have access to the position vectors of all partial atomic charges in the system as a function of time. One might easily determine the electrostatic potential from these charges, rather than resorting to the approximate GC theory as in the discussion above. To this end we make the simplifying assumption that the lateral (xy) components of the electric field are constant. This is a reasonable assumption, because PS was randomly distributed in the monolayers of the mixed bilayer in each simulation. This simplifying assumption enables us to reduce the problem to one dimension. Furthermore, we made use of the symmetry in a bilayer system by averaging the charge distribution over both bilayer leaflets. Thus, the total potential for each system as a function of the bilayer normal, z (shown in Figs. 13 a and 14 a), was calculated using the expression below,
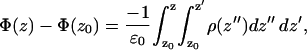 |
(1) |
such that z0 is a reference point in the bulk electrolyte where the potential is taken to be zero.
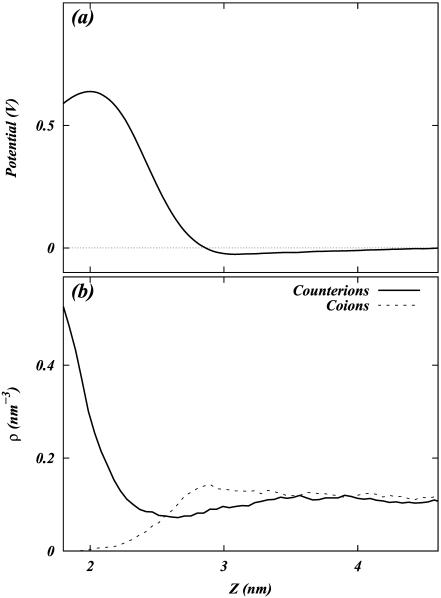
FIGURE 13.
(a) Total electrostatic potential profile of the S2 system as a function of z. (b) Density profile of co- and counterions as a function of z in the S2 system.
FIGURE 14.
(a) Total electrostatic potential profile of the S1 system as a function of z. (b) Density profile of co- and counterions as a function of z in the S1 system.
Upon observing these potential profiles, it is seen that, indeed, a negative potential exists at ∼3.0 nm from the center of the bilayer with respect to the bulk. However, an interesting discrepancy arises when comparing the value of the surface potential obtained from GC theory to the corresponding value resulting from Eq. 1. The surface used in the calculation of the GC surface potential, 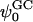 , was taken to be the plane where the cations lose half of their hydration shells (∼1.8 nm from the center of the bilayer). Again, this implies the usage of our ion-hydration criterion for ion binding. At this plane, both Figs. 13 a and 14 a display a potential that is nearly +600 mV with respect to the bulk. There is a blatant discrepancy between this value and that calculated for
, was taken to be the plane where the cations lose half of their hydration shells (∼1.8 nm from the center of the bilayer). Again, this implies the usage of our ion-hydration criterion for ion binding. At this plane, both Figs. 13 a and 14 a display a potential that is nearly +600 mV with respect to the bulk. There is a blatant discrepancy between this value and that calculated for 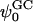 in Table 2. The observed very large positive potential at this “dehydration plane” is due to the dominance of the dipole potential at the interface. However, at larger values of z, the dipole potential decays rapidly (within ∼10 Å) and the tail of the potential profile shows the expected small negative value.
in Table 2. The observed very large positive potential at this “dehydration plane” is due to the dominance of the dipole potential at the interface. However, at larger values of z, the dipole potential decays rapidly (within ∼10 Å) and the tail of the potential profile shows the expected small negative value.
Apart from the electrostatic potential, the GC theory also predicts the density profile of ions as a function of the normal to a charged planar surface. The distributions of ions according to GC theory are determined by the surface potential and the Debye length. This Debye length is dependent upon the dielectric constant of the medium (usually taken to be 80 for bulk water) and the ionic strength of the solution. The observed deviation from GC behavior of the surface potential near the membrane surface spurred us to investigate the ion densities near the dehydration plane. These densities are shown in Figs. 13 b and 14 b. Note that neither the S2 nor the S1 systems show behavior that is similar to that of GC theory (assuming that the dielectric constant of water is 80 and 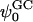 is −19 mV). In fact, Fig. 13 b shows significant charge inversion (Carnie and Torrie, 1984) in the distribution of counter- and co-ions. Fig. 14 b also shows a slight charge inversion, but this behavior is within the fluctuations of the ion densities.
is −19 mV). In fact, Fig. 13 b shows significant charge inversion (Carnie and Torrie, 1984) in the distribution of counter- and co-ions. Fig. 14 b also shows a slight charge inversion, but this behavior is within the fluctuations of the ion densities.
It is reasonable to conclude that the dipole potential is responsible for our systems' electrostatic deviations from the GC theory prediction. The behavior of the electrostatic potential in the region proximal to the bilayer surface is governed by the extreme polarization of water near the headgroups (Lin et al., 2002; Pandit et al., 2003a). This polarization effect can lead to a situation where water cannot be treated as a simple, homogenous, dielectric continuum with a dielectric constant of 80. The absence of such a homogenous dielectric can also lead to ionic distributions whose behavior deviates from that predicted by GC theory.
Typically, deviations from the GC theory are investigated by incorporating ion-ion correlations (Carnie and Torrie, 1984). One can find various possible explanations for the observed deviation from GC behavior. However, the assumption that water is a dielectric continuum is pivotal in the success of GC theory in describing the electrostatic properties of electrolyte near a charged wall. If the dielectric properties of water near the surface deviate from those expected in a homogenous continuum dielectric, grounds for questioning the usage of the theory would be apparent. This sort of deviation has been shown in previous work (Pandit et al., 2003a), where it was found that the properties of water in the region between z ≈ 1.8 nm and z ≈ 3.0 nm are not bulk-like. Therefore, at values >z ≈ 3.0 nm, one might expect ionic distributions and electrostatic potential profiles that more closely resemble those predicted by GC theory.
SUMMARY
We simulated two DPPC:DPPS (5:1) bilayer mixture systems, with two objectives. On one hand, we aimed to probe the ways in which DPPC and DPPS might interact to form complexes. It is seen in experimental studies that PC and PS form phase-separated domains in the presence of divalent ions. Although our simulations include only monovalent ions, it is still possible to study the lipid-lipid and ion-lipid interactions that may give rise to domain formation. This is important because MD simulation is capable of providing many molecular details of interaction. On the other hand, we also studied the electrostatic properties of the charged bilayer/electrolyte interface. Usually, these properties are studied using the continuum GC theory (Peitzsch et al., 1995; Murray et al., 1999), but a detailed molecular description is currently lacking.
Two direct binding modes were seen to occur between DPPC and DPPS molecules in the simulated systems. One of these involved a CH···O hydrogen bond, whereas the other involved an NH···O hydrogen bond. We observed DPPC to participate in much smaller lipid complexes (0:1–2:1) than DPPS (2:1–6:1) in both S1 and S2 systems. Furthermore, upon the comparison of results from the S1 and S2 systems to simulations of a pure DPPC bilayer with and without salt, it is observed that DPPC increases its propensity to form larger complexes when there is an electrolytic surrounding bath or when there is DPPS present in the bilayer. Another simulation study has shown that DPPC possesses the ability to form large complexes in bilayers where cholesterol is present (S. A. Pandit, D. Bostick, and M. L. Berkowitz, unpublished results). One might infer from these combined results that DPPC alone does not exhibit a tendency to form large complexes, where, in the presence of impurities, it does. Indeed, the ions' interactions with the DPPC headgroups of our systems seem to have a similar effect on the DPPC complexation propensity to that brought on by its direct interaction with cholesterol found in a previous simulation study (S. A. Pandit, D. Bostick, and M. L. Berkowitz, unpublished results). We have shown in this work that ions' ability to alter the complexation propensity of PC and PS is linked to the fact that they cause particular changes in the lipid headgroup conformation. These changes facilitate complexation with other lipids through a CH···O or NH···O hydrogen bond.
Will the presence of the ions induce a phase separation of lipids in the mixtures? How does the phase separation depend on the specific character of the ions or the specific nature of the lipids in the mixture? The present simulations do not provide us with answers to these questions due to the limited timescale of our simulations. This study does show, however, that the presence of ions enhances the interactions between the lipids in the bilayer.
To study the electrostatic properties of our simulated bilayer/electrolyte interface, it was necessary to determine the number of ions bound to the membrane surface. We studied two ways in which one might determine the number of bound ions, and consequently, the ionic binding constants. We proposed that an ion can be considered to be bound if and only if it is involved in a lipid-bridging event. It was found that this criterion gave a result similar to that employing a dehydration criterion proposed elsewhere (Pandit et al., 2003b). Both criteria provided reasonable binding constant values (listed in Table 1).
Upon using the determined number of bound ions for each system to derive a value for the membrane surface charge, we calculated the GC surface potential. Our values (Table 2) were close to those determined by electrophoretic mobility experiments (Winiski et al., 1986). We observed that the value of the potential at the dehydration surface obtained by twice integrating the excess charge density was large and positive ( +600 mV). The calculated potential profiles (Figs. 13 a and 14 a) show that the dipole potential dominates in the region of the dehydration plane (z ≈ 1.8 nm from the center of the bilayer). However, after the rapid decay of the dipole potential (over the range of ∼10 Å), the tail of the potential profiles shows the expected small negative value. Hence, our results show a qualitative agreement with GC theory for distances above ∼10 Å from the bilayer surface. It is well known that for distances less than this, water does not exhibit bulk-like properties. The water in this region cannot be expected to behave as though it were a homogenous, dielectric continuum. Moreover, in its simplest form, the GC theory assumes that the membrane/aqueous solution interface is planar with zero width. Recent simulations mostly performed on neutral phospholipid bilayers and the present simulations clearly demonstrate that the width of the water/membrane interface and structure of the interface cannot be neglected since the interface represents a large portion of the system under consideration.
Our simulations indicate that although the GC theory may give a qualitative picture of the electrostatic potential for adequate distances from the bilayer surface, it is liable to fail for distances <∼10 Å from this surface. We attribute the failure to the noncontinuous and nonbulk-like properties of water in this region and to the broad and complicated structure of the bilayer/electrolyte interface.
Acknowledgments
Computational support from the North Carolina Supercomputing Center is gratefully acknowledged.
This work was supported by the National Science Foundation under grant MCB0077499 and also in part by the Molecular and Cellular Biophysics Program at the University of North Carolina at Chapel Hill under the United States Public Health Service training grant T32 GM08570.
Sagar A. Pandit's present address is Department of Biological, Chemical, and Physical Sciences, Illinois Institute of Technology, 3101 S. Dearborn, Chicago, IL 60616.
References
- Berendsen, H., D. van der Spoel, and R. van Drunen. 1995. GROMACS: a message-passing parallel molecular dynamics implementation. Comp. Phys. Comm. 91:43–56. [Google Scholar]
- Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boda, D., K.-Y. Chan, and D. Henderson. 1998. Monte Carlo simulation of an ion-dipole mixture as a model of an electrical double layer. J. Chem. Phys. 109:7362–7371. [Google Scholar]
- Boda, D., D. Henderson, A. Patrykiejew, and S. Sokolowski. 2000. Simulation and density functional study of simple membrane. II. Solvent effects using the solvent primitive model. J. Chem. Phys. 113:802–806. [Google Scholar]
- Boda, D., D. Henderson, R. Rowley, and S. Sokolowski. 1999. Simulation and density functional study of a simple membrane separating two restricted primitive model electrolytes. J. Chem. Phys. 111:9382–9388. [Google Scholar]
- Carnie, S. L., and G. M. Torrie. 1984. The statistical mechanics of the electrical double layer. Adv. Chem. Phys. 56:141–253. [Google Scholar]
- Cevc, G. 1990. Membrane electrostatics. Biochim. Biophys. Acta. 1031:311–382. [DOI] [PubMed] [Google Scholar]
- Crozier, P. S., R. L. Rowley, and D. Henderson. 2001. Molecular-dynamics simulation of ion size effects on the fluid structure of aqueous electrolyte systems between charged model electrodes. J. Chem. Phys. 114:7513–7517. [Google Scholar]
- Desiraju, G. R. 1991. The C-H···O hydrogen bond in crystals: What is it? Acc. Chem. Res. 24:290–296. [Google Scholar]
- Eisenberg, M., T. Gresalfi, T. Riccio, and S. McLaughlin. 1979. Adsorption of monovalent cations to bilayer membranes containing negative phospholipids. Biochemistry. 18:5213–5223. [DOI] [PubMed] [Google Scholar]
- Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- Greberg, H., R. Kjellander, and T. Åkesson. 1997. Ion-ion correlations in electric double layers from Monte Carlo simulations and integral equation calculations. Part 2. Case of added salt. Mol. Phys. 92:35–48. [Google Scholar]
- Gu, Y., T. Kar, and S. Scheiner. 1999. Fundamental properties of the CH···O interaction: Is it a true hydrogen bond? J. Am. Chem. Soc. 121:9411–9422. [Google Scholar]
- Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaige. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- Huang, J., J. E. Swanson, A. R. G. Dibble, A. K. Hinderliter, and G. W. Feigenson. 1993. Nonideal mixing of phosphatidylserine and phosphatidylcholine in fluid lamellar phase. Biophys. J. 64:413–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Israelachvili, J. 1992. Intermolecular and Surface Forces, 2nd ed. Academic Press, San Diego, CA.
- Jacobson, K., and D. Papahadjopoulos. 1975. Phase transitions and phase separations in phospholipid membranes induced by changes in temperature, pH, and concentration of bivalent cations. Biochemistry. 14:152–161. [DOI] [PubMed] [Google Scholar]
- Jeffrey, G. A. 1997. An Introduction to Hydrogen Bonding. Oxford University Press, New York.
- Jorgensen, W. L., and J. Gao. 1986. Monte Carlo simulations of the hydration of ammonium and carboxylate ions. J. Am. Phys. Soc. 90:2174–2182. [Google Scholar]
- Lin, J.-H., N. A. Baker, and J. A. McCammon. 2002. Bridging implicit and explicit solvent approaches for membrane electrostatics. Biophys. J. 83:1374–1379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
- Lukatsky, D. B., S. A. Safran, A. W. C. Lau, and P. Pincus. 2002. Enhanced counterion localization induced by surface charge modulation. Europhys. Lett. 58:785–791. [Google Scholar]
- Luna, E. J., and H. M. McConnell. 1977. Lateral phase separations in binary mixtures of phospholipids having different charges and different crystalline structures. Biochim. Biophys. Acta. 470:303–316. [DOI] [PubMed] [Google Scholar]
- Marrink, S.-J., M. L. Berkowitz, and H. J. C. Berendsen. 1993. Molecular dynamics simulation of a membrane/water interface: the ordering of water and its relation to the hydration force. Langmuir. 9:3122–3131. [Google Scholar]
-
Mar
 elja, S. 2000. Exact description of aqueous electrical double layers. Langmuir. 16:6081–6083. [Google Scholar]
elja, S. 2000. Exact description of aqueous electrical double layers. Langmuir. 16:6081–6083. [Google Scholar] - McLaughlin, S. 1977. Membrane potentials at membrane-solution interfaces. Curr. Top. Membrane Transport. 9:71–144. [Google Scholar]
- McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
- McLaughlin, S., and A. Aderem. 1995. The myristoyl-electrostatic switch—a modulator of reversible protein-membrane interactions. Trends Biochem. Sci. 20:272–276. [DOI] [PubMed] [Google Scholar]
- Murray, D., A. Arbuzova, G. Hangyás-Mihályné, A. Gambhir, N. Ben-Tal, B. Honig, and S. McLaughlin. 1999. Electrostatic properties of membranes containing acidic lipids and adsorbed basic peptides: theory and experiment. Biophys. J. 77:3176–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nose, S., and M. L. Klein. 1983. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 50:1055–1076. [Google Scholar]
- Pandit, S. A., D. Bostick, and M. L. Berkowitz. 2003a. An algorithm to describe molecular scale rugged surfaces and its application to the study of a water/lipid bilayer interface. J. Chem. Phys. 119:2199–2205. [Google Scholar]
- Pandit, S. A., D. Bostick, and M. L. Berkowitz. 2003b. Molecular dynamics simulation of a dipalmitoylphosphatidylcholine bilayer with NaCl. Biophys. J. 84:3743–3750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parrinello, M., and A. Rahman. 1981. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 52:7182–7190. [Google Scholar]
- Peitzsch, R. M., M. Eisenberg, K. A. Sharp, and S. McLaughlin. 1995. Calculations of the electrostatic potential adjacent to model phospholipid bilayers. Biophys. J. 68:729–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raveendran, P., and S. L. Wallen. 2002. Cooperative C-H···O hydrogen bonding in CO2-Lewis base complexes: Implications for solvation in supercritical CO2. J. Am. Chem. Soc. 124:12590–12599. [DOI] [PubMed] [Google Scholar]
- Reviakine, I., A. Simon, and A. Brisson. 2000. Effect of Ca2+ on the morphology of mixed DPPC-DOPS supported phospholipid bilayers. Langmuir. 16:1473–1477. [Google Scholar]
- Smondyrev, A. M., and M. L. Berkowitz. 1999. United atom force field for phospholipid membranes: constant pressure molecular dynamics simulation of dipalmitoylphosphatidicholine/water system. J. Comput. Chem. 50:531–545. [Google Scholar]
- Tatulian, S. A. 1987. Binding of alkaline-earth metal cations and some anions to phosphatidylcholine liposomes. Eur. J. Biochem. 170:413–420. [DOI] [PubMed] [Google Scholar]
- van Dijck, P. W. M., B. De Kruijff, A. J. Verkleij, and L. L. M. van Deenen. 1978. Comparative studies on the effects of pH and Ca2+ on bilayers of various negatively charged phospholipids and their mixtures with phosphatidylcholine. Biochim. Biophys. Acta. 512:84–96. [DOI] [PubMed] [Google Scholar]
- Winiski, A. P., A. C. McLaughlin, R. V. McDaniel, M. Eisenberg, and S. McLaughlin. 1986. An experimental test of the discreteness-of-charge effect in positive and negative lipid bilayers. Biochemistry. 25:8206–8214. [DOI] [PubMed] [Google Scholar]