Abstract
Escherichia coli RNA polymerase translocates along the DNA discontinuously during the elongation phase of transcription, spending proportionally more time at some template positions, known as pause and arrest sites, than at others. Current models of elongation suggest that the enzyme backtracks at these locations, but the dynamics are unresolved. Here, we study the role of lateral displacement in pausing and arrest by applying force to individually transcribing molecules. We find that an assisting mechanical force does not alter the translocation rate of the enzyme, but does reduce the efficiency of both pausing and arrest. Moreover, arrested molecules cannot be rescued by force, suggesting that arrest occurs by a bipartite mechanism: the enzyme backtracks along the DNA followed by a conformational change of the ternary complex (RNA polymerase, DNA and transcript), which cannot be reversed mechanically.
Escherichia coli RNA polymerase (RNAP) is a highly processive enzyme responsible for the transcription of DNA into RNA. The ternary elongation complex of DNA, RNAP and RNA is extremely stable, with RNAP capable of reaching speeds of 35 nucleotides per second as it translocates along the DNA (1). Despite this rapid translocation during elongation, RNAP is sensitive to the sequence it transcribes, displaying temporary (pauses) and permanent (arrests) halts to transcription, which are believed to play a role in the regulation of gene expression (2).
Transcriptional pauses and arrests can occur by various mechanisms but share common features. These features include the continued stability of the ternary elongation complex (3) and the displacement of the RNA 3′ end from the enzyme active site (4, 5). Kinetic evidence suggests that both pauses and arrests are kinetically off the main elongation pathway, and that pauses are intermediate between elongation and arrest states (4, 6–8):
Much of the information about pauses and arrests has come from biochemical footprinting and crosslinking studies on complexes walked to particular template positions. These studies have suggested that core RNA polymerase is, variously, a flexible enzyme, capable of undergoing inchworming motion (9–11); a rigid enzyme, capable of monotonic translocation (12); and a “sliding clamp” enzyme, capable of frequent backwards and forwards oscillations (13–15). Among these proposed models, the importance given to an RNA:DNA hybrid and to different protein–nucleic acid interactions to explain the stability of the complex varies (16). Within the sliding clamp model, protein–nucleic acid contacts confer stability to the ternary complex (through a protein clamp enclosing downstream DNA), whereas the RNA:DNA hybrid (of 8–12 bp) is responsible for accurately positioning the enzyme active site with the 3′ OH of nascent RNA (13, 15, 17). The recently obtained crystal structure of a bacterial RNA polymerase shows evidence of a downstream DNA-binding site, and suggests that an RNA:DNA hybrid of 8–9 bp is easily accommodated within the enzyme, which is consistent with the sliding clamp model (18, 19). This model proposes that upon arrest, the entire enzyme backtracks along the DNA template, maintaining both the size of its footprint and the RNA:DNA hybrid, with its backtracking distance constrained by nascent RNA (13, 14). This severe repositioning of the enzyme upon arrest does not necessitate a flexible enzyme.
The postulated backtracking of RNA polymerase at arrest sequences and, to a lesser extent, at pause sites (5) suggests that it might be possible to regulate the degree of transcriptional pausing and arrest by applying mechanical force directly on an RNAP molecule to aid its forward translocation and thus prevent or reduce its backtracking. This type of experiment is possible with single-molecule techniques, which previously have examined transcription by single RNA polymerases subjected to a load opposing the direction of transcription (7, 8, 20) or in the absence of significant external force (21–24). In this paper, we use a new “assisting” force geometry to push the enzyme in the downstream (transcriptional) direction. By assisting the enzyme mechanically and by comparing the results with previous results on the same template in the “opposing” force geometry (8), we seek to determine the role of lateral displacements in the various components of the elongation cycle (RNA synthesis, pausing, arrest). For example, if arrest involves simply a net displacement of the enzyme along the DNA template (with concomitant changes in nucleic acid pairing) without a significant conformational change of the ternary complex, it should be possible to alter both entry into and exit from the backtracked state by applying a mechanical force in the direction opposing backwards displacement. Additionally, it is not known whether backtracking occurs upon arrest during continuous elongation, in the presence of all NTPs, without first artificially stalling transcription. By performing these experiments in the presence of all four NTPs, we can examine the role of mechanical displacement in “natural” arrest states. In the present study, we investigate the effect of mechanical force on pausing and arrest, compare the effect of forces aiding and opposing transcription, and comment on the flexibility of RNAP in the context of the various models of RNA polymerase translocation.
Materials and Methods
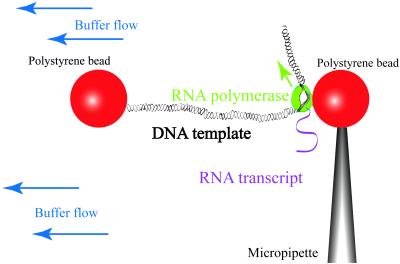
Previous work in our laboratory studied the effect of an opposing force on pausing and arrest (8). Our current studies on the effect of an assisting force use the same optical-trapping flow control video microscope (25) and a DNA template containing the same promoter and transcribed sequence. The template is derived from the pPIA2–6 plasmid (8) by digestions with PspOMI (upstream of the λ PR promoter) and either StuI or SnaBI to create a blunt downstream end. The upstream end is labeled by filling in the 5′ overhanging restriction site with biotinylated nucleotides. Ternary complexes are initially stalled by incubating biotinylated RNAP with the DNA in the presence of a subset of NTPs such that stalling occurs at position +70 (8). By using an optical trap, we tether a stalled complex between 2-μm streptavidin-coated polystyrene spheres in a flow cell. Then, we turn off the trap and flow in a buffer containing all four NTPs to restart transcription (Fig. 1). During transcription, a biotinylated RNAP moves away from the biotinylated upstream end of the DNA and toward its unlabeled downstream end, thus increasing the DNA tether length. By raising the flow speed in the microchamber, we increase the force applied on RNAP relative to the DNA, thus “pushing” the RNAP in the transcribing direction and assisting its forward translocation. In contrast, in the previous opposing-force experiments, the DNA was biotinylated downstream from the promoter and the application of higher forces increased the load opposing enzyme translocation. We obtain the DNA tether length (in bp) from bead-to-bead distance as described (8).
Figure 1.
Experimental setup (not to scale). As RNAP transcribes away from the labeled end of the DNA, the DNA tether between the two beads increases in length.
Results and Discussion
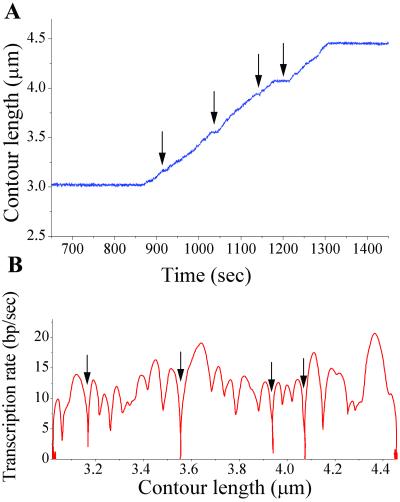
Fig. 2 shows representative assisting-force experimental data, illustrating that after the addition of NTPs to the tethered stalled elongation complex, tether length increases with time, which we interpret as transcription. The tether length was never observed to increase or decrease in the absence of NTPs. Fig. 2 also shows temporary halts to transcription, interpreted as pauses. Many molecules also arrest; an enzyme is considered arrested if it does not resume transcription within 10 min of entering a pause.
Figure 2.
(A) Change in tethered DNA contour length (calculated from bead-to-bead distance) during transcription by a single RNAP molecule, with pauses (temporary halts to transcription, arrows) and arrest (halt to transcription longer than 10 min; not all of the waiting time is shown here) clearly visible. (B) The transcription rate for the same transcription run, given by the derivative of low-pass filtered length vs. time data.
Current models of transcription entail a rate-limiting step that is biochemical (binding or catalysis) rather than mechanical (translocation) at subsaturating NTP concentrations (26, 27). This assumption is consistent with the results of single-molecule opposing-force experiments, where the transcription rate is force-independent until near the stall force of ≈15–25 pN (7, 8, 20). We wished to test these models by examining the effect of assisting force on the transcription rate.
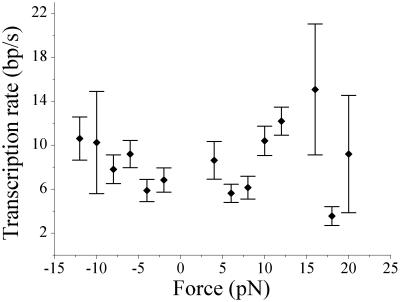
As can be seen in Fig. 2, the transcription rate varies along the template and exhibits minima at pause locations. We determined two different measures of transcription rates. The overall transcription rate, which considers only the length transcribed and the time taken to go from start to end, includes pauses. This value for the overall rate is given in Table 1 (voverall) and is strongly force- and NTP-dependent. To determine a transcription rate free of the influence of pausing, we consider only the peak rates of transcription attained between pauses separated by times greater than the resolution of our data-filtration technique (vmax in Table 1). These rates are broadly distributed, as is characteristic of single-molecule experiments. The force–velocity relationship obtained from these values for vmax at 200 μM NTPs is shown in Fig. 3 and encompasses both the opposing and assisting force data. This pause-free transcription rate (vmax) is independent of force. It does, however, increase with increasing NTP concentration, which is consistent with a biochemical rate-limiting step in this range of substrate concentrations. Thus, force in either direction does not seem to have a significant effect on translocation along the main transcription pathway.
Table 1.
Transcription rates
| NTP concentration | Opposing force
|
Assisting force
|
||
|---|---|---|---|---|
| 200 μM | 200 μM | 500 μM | 1 mM | |
| Overall transcription rate, voverall (bp/s)* | 3.6 ± 0.8 | 6.4 ± 0.8 | 9.7 ± 2.2 | 10.1 ± 1.1 |
| (N = 26) | (N = 26) | (N = 9) | (N = 26) | |
| Transcription rate free of pauses, vmax (bp/s)† | 7.9 ± 0.9 | 8.7 ± 1.0 | 12.0 ± 1.8 | 14.9 ± 1.5 |
| (N = 22) | (N = 24) | (N = 8) | (N = 26) | |
Average of the overall rate for each file, which includes pauses. Quoted error is the SEM for N transcription runs.
Maximum attainable transcription rate, determined by taking the peak rate between pauses separated by greater than the averaging window. Quoted error is the SEM for N transcription runs.
Figure 3.
The pause-free transcription rates (vmax) were determined at different forces for both opposing (negative) and assisting (positive) force at 200 μM NTPs and show no force dependence.
Effect of Force on Pausing.
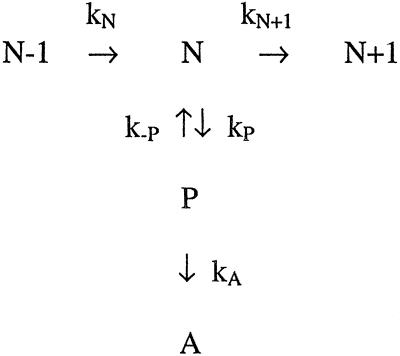
Although translocation is not the rate-determining step along the elongation pathway, the strong dependence of the overall rate (which includes pauses) on force strongly suggests that mechanical force can act on the off-pathway reaction leading to a pause (kP, Scheme S1). Such an effect is consistent with current models for pausing in which a lateral displacement of RNAP relative to the DNA template results in misalignment of the 3′ end of RNA from the catalytic center of the enzyme. Thus, transitions into a paused state should be force-dependent if the rate-limiting step to enter a pause involves this lateral movement of polymerase. To determine the effect of mechanical force on pausing, we consider its effect both on the entry into (kP) and exit from a pause (k−P), as can be obtained from the pause density (pauses per kb) and duration. Pauses give rise to minima in the transcription rate; to ensure that these minima correspond to true pauses rather than to artifacts of data sampling and filtering methods, we took only a subset of these minima that met additional criteria, verified by data simulation (see Supporting Text, which is published as supporting information on the PNAS web site, www.pnas.org).
Scheme 1.
Two different observations suggest an effect of force on entry into the pause state, kP. First, the mean pause density with assisting force is about two-thirds of that with opposing force (Table 2). As NTP concentration increases, the pause density with assisting force decreases further, showing that closer to saturation, RNAP pauses less frequently, consistent with results from bulk biochemistry. This decrease in pause density (per unit length) with increasing NTPs is not due solely to a decrease in time spent waiting at each nucleotide position: a time-based pause density (pauses per 1,000 s on the main elongation pathway) also decreases with increasing NTP (Table 2), suggesting that NTP concentration directly affects kP. Second, the fraction of molecules entering any detectable pauses during transcription decreases by more than a factor of two with an aiding force (Table 2). Assuming stochastic entry into a pause, a force-independent pausing mechanism would predict a decrease in the percentage of pause-free runs with an increase in length transcribed. Instead, an assisting force increases both the mean transcription length and the fraction of pause-free runs compared with opposing force, providing additional evidence that an assisting force exerts a considerable effect on entry into a pause. As discussed above, force does not affect the kinetics along the main elongation pathway (kN, Scheme S1), implying that the reduction in pausing that we observe is not caused by changes in the competing rates of pausing and elongation, but by the direct action of force on the off-pathway transition into the pause state (kP, Scheme S1).
Table 2.
Pausing statistics
| NTP concentration | Opposing force
|
Assisting force
|
||
|---|---|---|---|---|
| 200 μM | 200 μM | 500 μM | 1 mM | |
| Mean pause density (pauses/kb)* | 1.8 ± 0.3 (N = 26) | 1.4 ± 0.4 (N = 26) | 1.6 ± 1.1 (N = 9) | 0.6 ± 0.2 (N = 26) |
| Mean pause density (pauses/1,000 sec)† | 11.4 ± 1.1 | 7.9 ± 1.8 | 9.3 ± 3.0 | 4.7 ± 1.0 |
| Fraction of molecules with no detected pauses | 15% | 42% | 33% | 42% |
| Pause half life (sec)‡ | 78 ± 34 | 40 ± 15 | 30 ± 12 | 31 ± 12 |
| Pause duration (sec)§ | 90 ± 14 | 86 ± 27 | 45 ± 11 | 102 ± 35 |
The pause density was calculated for each transcription run from the number of pauses divided by the length transcribed. The quoted error is the SEM for N transcription runs.
This represents the likelihood of entering a pause state per time spent actively transcribing. It is calculated for each transcription run by multiplying the pause density (/kb) by the maximum transcription rate (vmax). Quoted error is the SEM.
Given by the time for 1/2 of the paused molecules to resume transcription, assuming first-order kinetics. Quoted error is SE of three different bins of fit determination (3s, 5s, 10s).
This estimate for pause duration divides the total time a molecule spends off-pathway in pause states by the number of pauses detected. The off-pathway time is calculated from the length transcribed (L), voverall, and vmax: t off = L (1/voverall − 1/vmax), as described in the text. Quoted error is the SEM.
The effect of force on exit from a pause to return to the main elongation pathway (k−P) can be studied by examining the pause durations. Again, we have accessed this in two ways. First, we determined the duration of each pause (see Supporting Text), then calculated a mean pause half-life by fitting to first-order decay kinetics. These values for pause half-lives are given in Table 2 and exhibit a slight dependence on force direction. It is difficult, however, to determine precisely the duration of a pause, whereas pause locations are easier to score. Thus, to obtain a more reliable estimate of the pause durations, we used the strongly force-dependent overall transcription rates (voverall) and the force-independent peak transcription rates between pauses (vmax). The time a given polymerase spends actively transcribing a length L is given by L/vmax; the actual time it takes to traverse this length L in an experiment is L/voverall. The difference between the active and overall transcription times gives the total time spent off-pathway in a pause state and reflects both the pause density and pause duration; dividing this total time by the number of pauses gives the mean pause duration. These values for pause durations, listed in Table 2, appear independent of force. Thus, it seems that the rate of return to the main elongation pathway, k−P, is either very weakly or not at all force-dependent.
At first glance, there is an apparent contradiction in the force dependence between entry into and exit from the paused state. Pausing is a reversible process, implying that the forward and reverse reactions traverse the same coordinate. How can traversal of this coordinate in one direction be force-dependent whereas force apparently has little affect on the reverse process? The rate of a force-dependent process scales exponentially with force applied and distance to the transition state (28). With an asymmetrically located transition state, the effect of force on reaction rate can be orders of magnitude stronger in one direction than in the other (see Supporting Text), easily accounting for the difference in force dependence between kP and k−P.
Effect of Force on Arrest.
Although RNAP has been shown to backtrack during arrest in stalled complexes formed by NTP deprivation, there is no evidence for backtracking into arrest during continuous elongation with all NTPs present. Previous single-molecule experiments using the same template as in this study showed that in the presence of an opposing load, all RNAP molecules arrested before arriving to the end of the template (10.7 kb from the transcription start site) at both 200 μM and 1 mM NTPs (8). Arrest in these experiments is not due to cumulative photodamage of the enzyme, as the optical trap is turned off as soon as a ternary complex is tethered, before resuming transcription. Given the putative large displacement involved in backtracking, arrest of actively transcribing complexes should display significant force dependence, assuming that the rate-limiting step to entry into arrest involves backtracking of the enzyme over this distance. Specifically, mechanical force opposing transcription should enhance the efficiency of backtracking into an arrested state, whereas assisting force should reduce backtracking and, hence, arrest.
Indeed, mechanically assisting transcription markedly reduces the incidence of arrest compared with transcription subjected to a load (Table 3). Even at 200 μM NTPs, fewer than 60% of the molecules arrest under assisting force, and this value decreases to less than 25% as the NTP concentration increases to 1 mM. The arrest density (total arrests per total length transcribed) also exhibits a significant force dependence (Table 3): the arrest density at 200 μM NTP decreases from 0.87 arrests per kb (opposing force) to 0.30 arrests per kb (assisting force). As mentioned earlier, current kinetic models for transcription elongation suggest that arrests are preceded by pausing intermediates. Given the effect of assisting force in reducing the rate of entry into the pause state, it is possible that the reduction in arrest efficiency with assisting force results simply from reduced pause efficiency and not from a direct effect of mechanical force on entry into arrest (kA, Scheme S1). To address this possibility, we computed the effect on pause density (pauses per kb, ∝kP) and arrest density (arrests per kb, ∝kA) of assisting vs. opposing transcription with force. We found that, at 200 μM NTPs, the pause density with an assisting force is 78% of that with opposing force, whereas the arrest density is decreased much further, to 35% of the opposing force value (Tables 2 and 3). The stronger effect of force on arrest density than on pause density indicates that mechanical force acts directly on the rate of entry into the arrested state (kA). The strong effect of mechanical force on arrest efficiency can be rationalized if pushing the enzyme in the direction of transcription tilts the reaction coordinate to energetically disfavor backtracking into the arrested state. Furthermore, this strong force dependence implies that entry into arrest involves a displacement of RNAP, consistent with the backtracked arrest state previously described for stalled complexes.
Table 3.
Arrest statistics
| NTP concentration | Opposing force
|
Assisting force
|
||
|---|---|---|---|---|
| 200 μM | 200 μM | 500 μM | 1 mM | |
| Arrest frequency, % transcription runs* | 100% (N = 18) | 57% (N = 23) | 40% (N = 10) | 24% (N = 29) |
| Arrest density, arrests/kb† | 0.87 | 0.30 | 0.15 | 0.11 |
| Mean length transcribed, kb‡ | 1.8 ± 0.3 (N = 18) | 2.2 ± 0.3 (N = 23) | 2.6 ± 0.4 (N = 10) | 3.2 ± 0.2 (N = 29) |
The percentage of molecules that arrested (irreversibly halted for at least 10 minutes) before reaching the end of the template. N is the total number of molecules included in the statistics.
Calculated by dividing the total number of molecules that arrested by the total length transcribed (for those that arrested and those that transcribed to the end of the template).
Average distance transcribed before arrest or template run-off. Quoted error is the SEM. Note that the values for assisting force underestimate the potential length transcribed, as a significant fraction of enzymes reached the end of the template without arresting; for these, the length of the transcribed template was used as a lower estimate.
Having shown that applying an assisting force can prevent the arrest of the molecule during continuous elongation, we asked whether it is possible to rescue mechanically an already arrested ternary complex and return it to the main elongation pathway. For purified ternary complexes under standard biochemical reaction conditions, entry into the arrested state is an irreversible process, as arrested complexes cannot resume transcription without the addition of a transcript cleavage factor such as GreB (29, 30). This biochemical irreversibility does not imply that the reaction is mechanically irreversible: force could tilt the reaction coordinate, lowering the energetic barrier sufficiently to allow forward displacement of the enzyme. To test this idea, complexes in which elongation had ceased for at least 10 minutes, i.e., arrested by our definition, were subjected to increasing force in the forward direction. These efforts proved largely unsuccessful, with the enzyme resuming transcription in less than 10% of the cases (3 of 41 attempted rescues).
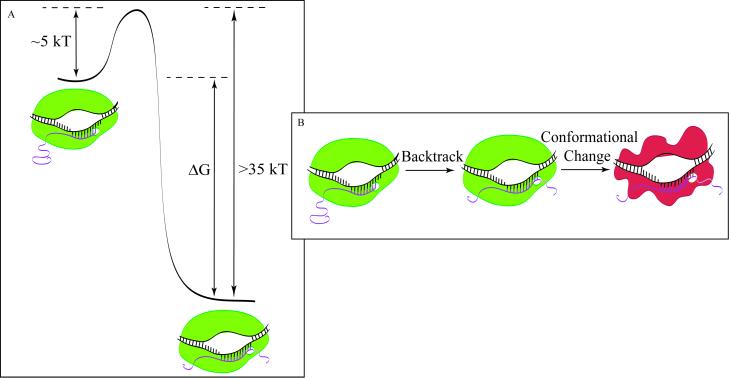
Is this inability to rescue arrested complexes due solely to the existence of a large energetic barrier to forward displacement? Forces up to 50 pN were applied to the arrested complexes in the above experiments, which, if acting over a distance of 10 bp (the estimated extent of the backtrack; ref. 31), results in ≈40 kBT of work. (The maximum of ≈50 pN of force available in our instrument is very close to the upper limit of 65 pN that can be applied to double-stranded DNA before it undergoes an overstretching transition to a different structural form; ref. 32.) If the arrested enzyme is simply mechanically displaced, i.e., if the reaction coordinate to arrest involves only a displacement of the enzyme along the DNA, the failure to rescue arrested complexes implies that an exceptionally high energetic barrier must be overcome to resume elongation, which is consistent with the irreversibility of arrest in bulk assays. However, because RNAP can enter into arrest under thermal conditions, the energetic barrier leading to arrest at those template locations must be on the order of at most a few kBT (Fig. 4). Again, assuming that the reaction coordinate for entry into and exit from arrest is the relative position of RNAP along the DNA template, the free energy difference between the active state and the arrested, backtracked state of the enzyme would be a minimum of ≈35 kBT. This number is unreasonably large, because it would imply an energetic stabilization upon backtracking by an amount greater than the overall binding energy of RNAP to DNA (≈25 kBT; ref. 33). This absurd result suggests, instead, that the reaction coordinate for arrest is not simply a displacement of the RNAP along the DNA. Rather, it is likely that a force-independent conformational change of the enzyme or ternary complex occurs after backtracking, and that this conformational change is off the mechanical reaction coordinate, effectively rendering the overall process mechanically irreversible.
Figure 4.
(A) Reaction coordinate for polymerase entering arrest by mechanical displacement only. For illustration purposes, we assume that the barrier to arrest is equal to 5 kBT. (B) Depiction of entry into arrest by backtracking followed by a structural reorganization.
What is the nature of this structural reorganization of the ternary complex after backtracking? Zaychikov et al. (34) studied active and arrested ternary complexes and found a significant increase in gel mobility upon arrest, which they interpreted as a change in DNA-bending angle leading to a more extended conformation. Crosslinking studies of arrested and productive elongation complexes have shown a change in interactions between the 3′ end of the RNA and polymerase upon arrest and demonstrated that unwound 3′-proximal RNA feeds into the secondary channel of RNAP (19, 35). It is unlikely that a change in RNA location alone would be sufficient to prevent mechanical repositioning of the polymerase and would account for the large energetic barrier to reactivation of transcriptional elongation. It is more likely that the change in contacts between RNA and the polymerase exerts an allosteric effect on the enzyme, triggering a conformational change away from the active configuration. The rescue of arrested complexes by GreB could be caused as much by the removal of the extruded 3′ RNA as by the removal of its allosteric contact with the polymerase.
Does the backtracking of RNAP automatically induce this structural reorganization of the ternary complex; i.e., are the two components of arrest tightly coupled? In a tight coupling scheme, translocation of the enzyme is accompanied by the simultaneous structural reorganization of the complex. A number of observations suggest that this is not the case. For example, bulk biochemical studies showed that backtracked enzymes are still capable of resuming active transcription at some locations (14). Thus, it is plausible that, upon backtracking, the complex is initially in a displaced intermediate state from which it then undergoes a structural reorganization as described above. This last step should be a mechanically irreversible change that prevents mechanical rescue of the complex to the elongation competent form. From the pause durations observed, we conclude that conversion to a transcriptionally inactive form takes place over the course of minutes at room temperature with the NTP concentrations used in this study (200 μM to 1 mM). To test the model of backtracking followed by mechanically irreversible change, we subjected complexes that had ceased transcription for various amounts of time to varying strengths of assisting force. The results of these rescue attempts are shown in Table 4. Complexes are most likely to be rescued mechanically when they have ceased transcription for less than 5 min. As the delay time is increased before applying greater assisting force on the enzyme, the rescue efficiency decreases, until, finally, for waiting times longer than 12 min, we are unable to rescue any complex mechanically. As controls, the lifetimes of pauses for which we did not increase the force after cessation of transcription were determined. With no increase in initial force, the longest pause observed was 400 s, and the average pause duration was 122 s, whereas with an increase in assisting force, the longest pause rescued was 765 s and the average waiting time before successful rescues was 296 s. Thus, an increase in assisting mechanical force can access and rescue complexes that would otherwise become irreversibly arrested. Most importantly, the ability to rescue an arrested enzyme decreases with waiting time, suggesting that we can mechanically rescue complexes that are paused and possibly backtracked but not those that have undergone an irreversible conformational change into the arrested state (Fig. 5).
Table 4.
Mechanical rescue of paused molecules
| 0–5 min | 5–10 min | 10–15 min | >15 min | |
|---|---|---|---|---|
| N rescued | 9 | 2 | 3 | 0 |
| N failed | 22 | 18 | 22 | 19 |
| Success rate, % | 29 | 10 | 12 | 0 |
A pause was deemed “rescued” if, following an increase in applied assisting force, there was an immediate resumption of transcription. This table combines results from all NTP concentrations; we have found no effect of NTP concentration on our ability to rescue paused molecules, although our current statistics at 1 mM NTP are poor because of the much lower pause and arrest density and, therefore, fewer possibilities to attempt a rescue.
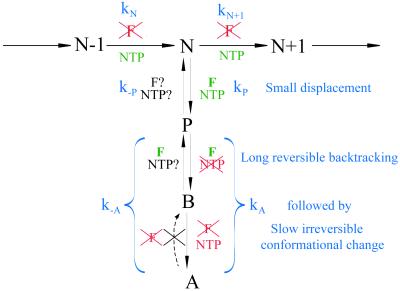
Figure 5.
Kinetic scheme for the elongation cycle, with associated force- and NTP-dependences of the rates. N−1, N, and N + 1 refer to consecutive steps in the main elongation pathway; P is a pause state, B is backtracked (prearrest), and A is arrest. The proposed changes associated with each step are shown in blue, as discussed in the text.
Kinetic Cycle of Transcription Elongation.
The results of this study allow us to determine the roles of mechanical and chemical forces on the various steps of the elongation cycle. Fig. 5 shows the kinetic scheme for RNA synthesis, pausing, and arrest given in our introductory remarks, including the role of force and NTP concentration determined in this study. Consistent with earlier studies, we have found the transcription rate to be force-independent but NTP-dependent. A reduction in NTP concentration leads to more frequent off-pathway excursions, manifest in an increased pause density. This result is consistent with the results of bulk biochemical assays (27), in which pause efficiencies are enhanced at lower NTP concentrations, and with the scheme of Fig. 5, in which pausing and elongation compete kinetically. The pause density depends also on the sense (assisting or opposing) of applied force, suggesting that at least a subset of pauses involves displacement of RNAP relative to the DNA template. The stronger effect of force on arrest efficiency lends support to the model of a displaced enzyme in the arrest state and suggests that this displacement is significantly larger than in paused states. The large scale of enzyme backtracking is evidenced by our ability to decrease the incidence of arrest and increase the mean length transcribed by the application of an assisting force and by the fact that even with the smallest of opposing forces (<2 pN), the transcribed length is reduced relative to that with small assisting forces, indicating premature arrest of the polymerase. Interestingly, the process of arrest seems to occur by a bipartite mechanism. First, the enzyme undergoes backtracking into an intermediate state (B, Fig. 5), which can be mechanically restored to elongation. This backtracking is followed by the kinetically slower step of a structural reorganization within the ternary elongation complex. Apparently, the conformational transition to the arrested state cannot be affected by force, as we cannot rescue complexes that have been transcriptionally inactive for longer than 12 min. Therefore, it seems that this arrested state can be restored to the active configuration only by biochemical means, after cleavage of downstream RNA by a factor such as GreB (29, 30).
Elongation Models.
The stability of the ternary complex at the end of the template has important implications for models of elongation. At the last position on blunt-ended DNA, there is no interaction between DNA and regions of the polymerase downstream of the active site (the downstream DNA-binding site in the inchworm model, the protein clamp in the sliding clamp model). Thus, the only interactions maintaining the ternary complex are with and within the RNA:DNA hybrid and with upstream DNA- and RNA-binding sites. The majority (84%) of RNAP molecules that reached the blunt downstream end of the DNA in our assisting-force experiments detached from the template. An analysis of the times spent at the end of the template before dissociation gives a half-life of approximately 40 s, a value comparable to the half-life of ternary complexes at the end of a blunt template determined in bulk biochemical experiments (36). We have found no force-dependent trend to these lifetimes in our study, suggesting that mechanical force exerts no significant effect on the stability of these ternary complexes. Our inability to drastically affect these interactions by the application of an assisting force probably reflects the fact that, in the absence of protein–downstream DNA interactions, lateral forces maintaining the polymerase along DNA are still significant.
We have shown that transcriptional arrest can occur during continuous elongation and at NTP concentrations near saturation, even when a mechanical force is acting to prevent backtracking of RNAP. Nonetheless the incidence of arrest is greatly inhibited by an assisting force and by increasing NTP concentrations. Models of a rigid enzyme suggest that entry into the backtracked, arrested state is driven by hybrid energetics. For example, studies that have modified the hydrogen-bonding within the RNA:DNA hybrid affect its stability and the incidence of backtracking (13). The strong effect of force on arrest suggests that the transition from paused to backtracked complexes involves a large displacement, implying that the enzyme does not populate intermediate states between these two configurations.
The experiments outlined in this paper have demonstrated that the application of force can play a unique role in determining the range of polymerase displacement occurring during transcription. That the enzyme can continue not only to grip the DNA but also to transcribe at an NTP-determined rate, even at such high assisting forces as 50 pN, is an impressive feat. It is still not known what the minimal step size of the enzyme is during transcription elongation, which is a crucial detail for discriminating among various models of RNAP translocation. The ability to observe transcription at high forces has direct implications for obtaining high-resolution information on the dynamics of RNA polymerase. More generally, the ability to access a higher range of forces by assisting a motor enzyme may help in gaining more information about the dynamics of other systems.
Supplementary Material
Acknowledgments
We thank Robert Landick for the gift of biotinylated RNA polymerase. We acknowledge helpful discussions with Zeu Bryant, John Davenport, Lillian Hsu, and Caroline Kane, and Errol Watson for assistance with template preparation. This research was supported by National Institutes of Health Grant 5R37GM032543-21, Department of Energy Grant DE-AC03-76SF00098, and by fellowships from the Natural Sciences and Engineering Research Council of Canada (to N.R.F.) and the European Molecular Biology Organization (to D.I.).
Abbreviation
- RNAP
RNA polymerase
References
- 1.Chamberlin M J, Nierman W C, Wiggs J, Neff N. J Biol Chem. 1979;254:61–69. [PubMed] [Google Scholar]
- 2.Uptain S M, Kane C M, Chamberlin M J. Annu Rev Biochem. 1997;66:117–172. doi: 10.1146/annurev.biochem.66.1.117. [DOI] [PubMed] [Google Scholar]
- 3.Arndt K M, Chamberlin M J. J Mol Biol. 1990;213:79–108. doi: 10.1016/S0022-2836(05)80123-8. [DOI] [PubMed] [Google Scholar]
- 4.Landick R. Science. 1999;284:598–599. doi: 10.1126/science.284.5414.598. [DOI] [PubMed] [Google Scholar]
- 5.Artsimovitch I, Landick R. Proc Natl Acad Sci USA. 2000;97:7090–7095. doi: 10.1073/pnas.97.13.7090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Erie D A, Hajiseyedjavadi O, Young M C, von Hippel P H. Science. 1993;262:867–873. doi: 10.1126/science.8235608. [DOI] [PubMed] [Google Scholar]
- 7.Wang M D, Schnitzer M J, Yin H, Landick R, Gelles J, Block S M. Science. 1998;282:902–907. doi: 10.1126/science.282.5390.902. [DOI] [PubMed] [Google Scholar]
- 8.Davenport R J, Wuite G J L, Landick R, Bustamante C. Science. 2000;287:2497–2500. doi: 10.1126/science.287.5462.2497. [DOI] [PubMed] [Google Scholar]
- 9.Chamberlin M J. Harvey Lect. 1995;88:1–21. [PubMed] [Google Scholar]
- 10.Krummel B, Chamberlin M J. J Mol Biol. 1992;225:239–250. doi: 10.1016/0022-2836(92)90918-a. [DOI] [PubMed] [Google Scholar]
- 11.Wang D G, Meier T I, Chan C L, Feng G H, Lee D N, Landick R. Cell. 1995;81:341–350. doi: 10.1016/0092-8674(95)90387-9. [DOI] [PubMed] [Google Scholar]
- 12.Yager T D, von Hippel P H. In: Escherichia coli and Salmonella typhimurium: Cellular and Molecular Biology. Neidhardt F C, editor. Washington, DC: Am. Soc. Microbiol.; 1987. [Google Scholar]
- 13.Nudler E, Mustaev A, Lukhtanov E, Goldfarb A. Cell. 1997;89:33–41. doi: 10.1016/s0092-8674(00)80180-4. [DOI] [PubMed] [Google Scholar]
- 14.Komissarova N, Kashlev M. J Biol Chem. 1997;272:15329–15338. doi: 10.1074/jbc.272.24.15329. [DOI] [PubMed] [Google Scholar]
- 15.Landick R. Cell. 2001;105:567–570. doi: 10.1016/s0092-8674(01)00381-6. [DOI] [PubMed] [Google Scholar]
- 16.Nudler E. J Mol Biol. 1999;288:1–12. doi: 10.1006/jmbi.1999.2641. [DOI] [PubMed] [Google Scholar]
- 17.von Hippel P H. Science. 1998;281:660–665. doi: 10.1126/science.281.5377.660. [DOI] [PubMed] [Google Scholar]
- 18.Zhang G Y, Campbell E A, Minakhin L, Richter C, Severinov K, Darst S A. Cell. 1999;98:811–824. doi: 10.1016/s0092-8674(00)81515-9. [DOI] [PubMed] [Google Scholar]
- 19.Korzheva N, Mustaev A, Kozlov M, Malhotra A, Nikiforov V, Goldfarb A, Darst S A. Science. 2000;289:619–625. doi: 10.1126/science.289.5479.619. [DOI] [PubMed] [Google Scholar]
- 20.Yin H, Wang M D, Svoboda K, Landick R, Block S M, Gelles J. Science. 1995;270:1653–1657. doi: 10.1126/science.270.5242.1653. [DOI] [PubMed] [Google Scholar]
- 21.Schafer D A, Gelles J, Sheetz M P, Landick R. Nature (London) 1991;352:444–448. doi: 10.1038/352444a0. [DOI] [PubMed] [Google Scholar]
- 22.Yin H, Landick R, Gelles J. Biophys J. 1994;67:2468–2478. doi: 10.1016/S0006-3495(94)80735-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yin H, Artsimovitch I, Landick R, Gelles J. Proc Natl Acad Sci USA. 1999;96:13124–13129. doi: 10.1073/pnas.96.23.13124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harada Y, Ohara O, Takatsuki A, Itoh H, Shimamoto N, Kinosita K. Nature (London) 2001;409:113–115. doi: 10.1038/35051126. [DOI] [PubMed] [Google Scholar]
- 25.Wuite G J L, Davenport R J, Rappaport A, Bustamante C. Biophys J. 2000;79:1155–1167. doi: 10.1016/S0006-3495(00)76369-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Erie D A, Yager T D, von Hippel P H. Annu Rev Biophys Biomol Struct. 1992;21:379–415. doi: 10.1146/annurev.bb.21.060192.002115. [DOI] [PubMed] [Google Scholar]
- 27.Foster J E, Holmes S F, Erie D A. Cell. 2001;106:243–252. doi: 10.1016/s0092-8674(01)00420-2. [DOI] [PubMed] [Google Scholar]
- 28. Tinoco, I., Jr., & Bustamante, C. (2002) Biophys. Chem., in press. [DOI] [PubMed]
- 29.Borukhov S, Sagitov V, Goldfarb A. Cell. 1993;72:459–466. doi: 10.1016/0092-8674(93)90121-6. [DOI] [PubMed] [Google Scholar]
- 30.Borukhov S, Laptenko O, Lee J. Methods Enzymol. 2001;342:64–76. doi: 10.1016/s0076-6879(01)42536-5. [DOI] [PubMed] [Google Scholar]
- 31.Komissarova N, Kashlev M. Proc Natl Acad Sci USA. 1997;94:1755–1760. doi: 10.1073/pnas.94.5.1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Smith S B, Cui Y J, Bustamante C. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 33.Chamberlin M. In: RNA Polymerase. Chamberlin M, Losick R, editors. Plainview, NY: Cold Spring Harbor Lab. Press; 1976. pp. 159–191. [Google Scholar]
- 34.Zaychikov E, Denissova L, Guckenberger R, Heumann H. Nucleic Acids Res. 1999;27:3645–3652. doi: 10.1093/nar/27.18.3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Markovtsov V, Mustaev A, Goldfarb A. Proc Natl Acad Sci USA. 1996;93:3221–3226. doi: 10.1073/pnas.93.8.3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nudler E, Avetissova E, Markovtsov V, Goldfarb A. Science. 1996;273:211–217. doi: 10.1126/science.273.5272.211. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.