Skip to main content
Springer Nature Link
Log in

The role of stress in the growth of a multicell spheroid

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract.

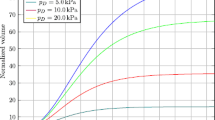
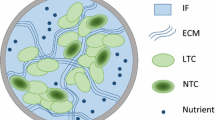
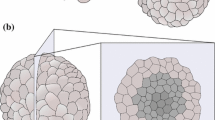
Rather recent experimental results demonstrate the non–negligible role of mechanical stress in the growth of a multicell spheroid. In this paper we discuss a theoretical framework for volumetric growth suitable for modeling the growth of soft tissues exhibiting the properties of a solid. After a proper kinematic decomposition, balance equations for mass, momentum and energy are discussed together with constitutive relationships. The mathematical model is then applied to avascular tumor growth. We show by numerical simulation that, under assumption of spherical symmetry, the mathematical model is able to reproduce the experimental data with a satisfying qualitative agreement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Canada)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ambrosi, D., Mollica, F.: On the mechanics of tumor growth. Int. J. Eng. Sci. 40, 1297–1316 (2002)

    Article  Google Scholar 

  2. Ambrosi, D., Preziosi, L.: On the closure of mass balance models of tumor growth. Math. Models Meth. Appl. Sci. 12, 737–754 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  3. Blatz, P.J., Ko, W.L.: Application of finite elasticity theory to the deformation of rubbery materials. Trans. Soc. Rheology 6, 223–251 (1962)

    Article  Google Scholar 

  4. Byrne, H.: Modelling avascular tumour growth. In: Cancer Modelling and Simulation. L. Preziosi (ed), Chapman & Hall/CRC, 2003

  5. Chen, C.Y., Byrne, H.M., King, J.R.: The influence of growth–induced stress from the surrounding medium on the development of multicell spheroids. J. Math. Biol. 43, 191–220 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  6. DiCarlo, A., Quiligotti, S.: Growth and balance. Mech. Res. Commun. 29, 449–456 (2002)

    Article  MATH  Google Scholar 

  7. Forgacs, G., Foty, R.A., Shafrir, Y., Steinberg, M.S.: Viscoelastic properties of living embryonic tissues: a quantitative study. Biophys. J. 74, 2227–2234 (1998)

    Google Scholar 

  8. Folkman, J., Hochbergand, M.: Self–regulation of growth in three dimensions. J. Exp. Med. 138, 745–753 (1973)

    Google Scholar 

  9. Greenspan, H.P.: Models for the growth of a solid tumour by diffusion. Stud. Appl. Math. 52, 317–340 (1972)

    Google Scholar 

  10. Gurtin, M.E.: An introduction to continuum mechanics. Academic Press, New York, 1981

  11. Helmlinger, G., Netti, P.A., Lichtenbeld, H.C., Melder, R.J., Jain, R.K.: Solid stress inhibits the growth of multicellular tumour spheroids. Nature Biotech. 15, 778–783 (1997)

    Google Scholar 

  12. Holmes, M.H.: Finite deformation of soft tissue: analysis of a mixture model in uni–axial compression. Transactions of the ASME 108, 372–381 (1986)

    Google Scholar 

  13. Humphrey, J.D.: Continuum biomechanics of soft biological tissues Proceedings of the Royal Society 459, 3–46 (2003)

  14. Klisch, S.M., Van Dyke, T.J., Hoger, A.: A theory of volumetric growth for compressible elastic biological materials. Math. Mech. Solids 6, 551–575 (2001)

    MATH  Google Scholar 

  15. Landman, K., Please, C.P.: Tumor dynamics and necrosis: surface tension and stability. IMA J. Math. Appl. Med. Biol. 18, 131–158 (2001)

    MATH  Google Scholar 

  16. Mollica, F., Rajagopal, K.R., Srinivasa, A.R.: The inelastic behavior of metals subject to loading reversal. Int. J. Plasticity 17, 1119–1146 (2001)

    Article  MATH  Google Scholar 

  17. Quarteroni, A., Valli, A.: Domain Decomposition Methods for Partial Differential Equations. Oxford University Press, New York, 1999

  18. Pioletti, D.P., Rakotomanana, L.R.: Non–linear viscoelastic laws for soft biological tissues. Eur. J. Mech. A/Solids 19, 749–759 (2000)

    Article  MATH  Google Scholar 

  19. Rajagopal, K.R., Srinivasa, A.R.: Mechanics of the inelastic behavior of materials. Part I: Theoretical underpinnings. Int. J. Plasticity 14, 945–967 (1998)

    Article  MATH  Google Scholar 

  20. Rajagopal, K.R., Srinivasa, A.R.: Mechanics of the inelastic behavior of materials. Part II: Inelastic response. Int. J. Plasticity 14, 969–995 (1998)

    Article  MATH  Google Scholar 

  21. Rodriguez, E.K., Hoger, A., McCulloch, A.: Stress dependent finite growth in soft elastic tissues. J. Biomechanics 27, 455–467 (1994)

    Article  Google Scholar 

  22. Skalak, R., Zargaryan, S., Jain, R.K., Netti, P.A., Hoger, A.: Compatibility and genesis of residual stress by volumetric growth. J. Math. Biol. 34, 889–914 (1996)

    Article  MATH  Google Scholar 

  23. Taber, L.: Biomechanics of growth, remodeling and morphogenesis. Appl. Mech. Rev. 48, 487–545 (1995)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Politecnico di Torino, corso Duca degli Abruzzi 24, 10129, Torino, Italy

    D. Ambrosi

  2. Dipartimentó di Ingegneria dei Materiali, via Saraget 1, 44100, Ferrara, Italy

    F. Mollica

Authors
  1. D. Ambrosi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Mollica
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. Ambrosi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ambrosi, D., Mollica, F. The role of stress in the growth of a multicell spheroid. J. Math. Biol. 48, 477–499 (2004). https://doi.org/10.1007/s00285-003-0238-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-003-0238-2

Keywords

Search

Navigation