Skip to main content
Springer Nature Link
Log in

Vibration attenuation on spur gears through optimal profile modification based on an alternative dynamic model

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

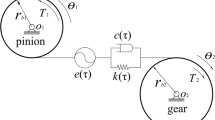
Abstract

The dynamic characteristic of a gear transmission system is an important parameter to define its quality. The variation in the number of teeth in contact during rotation of the gears has a large contribution to the vibrations of these systems. From this context, the need to evaluate the dynamic characteristics of the gear while it is still in the design phase is highlighted. In this work, the influence of addendum modification to the tooth profile of spur gears on the gear mesh vibration was studied. For this purpose, simulations were performed in order to determine an optimal value to the modification parameter capable of minimizing the vibrations. The model of the dynamic system used in this problem considers time-varying meshing stiffness and damping, and it includes an improvement to the equivalent mass calculation compared to other works in the field. It is shown that the amount of modification obtained for specified operating conditions presents optimal results only for those designed conditions, and its behavior degrades significantly if operating conditions change. From the comparison between the simulation results of the optimized and original system, it is concluded that the optimal modification brings the dynamic responses closer to the static ones, with change rates close to zero and nearly constant transmission error, providing minimal vibration to the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Canada)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Abbreviations

AGMA:

American Gear Manufacturers Association

BDF:

Backward differentiation formulae

CAD:

Computer aided design

DMF:

Dynamic meshing force

DTE:

Dynamic transmission error

EHL:

Elasto-hydrodynamic lubrication

FEA:

Finite element analysis

HPSTC:

Highest point of single tooth contact

LOA:

Line of action

LPSTC:

Lowest point of single tooth contact

LTCA:

Loaded tooth contact analysis

RMS:

Root mean square

TCA:

Tooth contact analysis

TE:

Theoretical transmission error

TPM:

Tooth profile modification

TVMD:

Time-varying meshing damping

TVMS:

Time-varying meshing stiffness

References

  1. Wang Y (2007) Optimized tooth profile based on identified gear dynamic model. Mech Mach Theory 42(8):1058–1068

    Article  Google Scholar 

  2. Hu Z, Tang J, Zhong J, Chen S, Yan H (2016) Effects of tooth profile modification on dynamic responses of a high speed gear-rotor-bearing system. Mech Syst Signal Process 76:294–318

    Article  Google Scholar 

  3. Ma H, Pang X, Feng R, Wen B (2016) Evaluation of optimum profile modification curves of profile shifted spur gears based on vibration responses. Mech Syst Signal Process 70:1131–1149

    Article  Google Scholar 

  4. Litvin FL, Lu J, Townsend D, Howkins M (1999) Computerized simulation of meshing of conventional helical involute gears and modification of geometry. Mech Mach Theory 34(1):123–147

    Article  Google Scholar 

  5. Wang C, Shi Z (2017) A dynamic calculation method of sliding friction losses for a helical gear pair. J Braz Soc Mech Sci Eng 39(5):1521–1528

    Article  Google Scholar 

  6. Wang C (2019) Optimization of tooth profile modification based on dynamic characteristics of helical gear pair. Iran J Sci Technol Trans Mech Eng 43(1):631–639

    Article  Google Scholar 

  7. Wang C (2021) Multi-objective optimal design of modification for helical gear. Mech Syst Signal Process 157:107762

    Article  Google Scholar 

  8. Wang C (2021) Study on 3-d modification for reducing vibration of helical gear based on tca technology, ltca technology and system dynamics. Mech Syst Signal Process 146:106991

    Article  Google Scholar 

  9. Gkimisis L, Vasileiou G, Sakaridis E, Spitas C, Spitas V (2021) A fast, non-implicit sdof model for spur gear dynamics. Mech Mach Theory 160:104279

    Article  Google Scholar 

  10. Yang D, Lin J (1987) Hertzian damping, tooth friction and bending elasticity in gear impact dynamics

  11. Ghosh S, Chakarborty G (2013) The influence of friction force on modified gear teeth and its effect on bearing force. In: 1st international and 16th national conference on machines and mechanisms, pp. 202–210. Indian Institute of Technology, Kharagpur, Roorkee

  12. Ghosh S, Chakraborty G (2016) On optimal tooth profile modification for reduction of vibration and noise in spur gear pairs. Mech Mach Theory 105:145–163

    Article  Google Scholar 

  13. Zhou R, Luo B, Li W (2022) A new dynamics modeling method for a spur gear pair with tooth profile modification. J Braz Soc Mech Sci Eng 44(9):438

    Article  Google Scholar 

  14. Shi JL, Ma XG, Xu CL, Zang SJ (2013) Meshing stiffness analysis of gear using the ishikawa method. In: Applied mechanics and materials, vol 401. Switzerland, pp 203–206 . Trans Tech Publications

  15. Budynas RG, Nisbett JK (2020) Shigley’s mechanical engineering design, vol 11. McGraw Hill, New York

    Google Scholar 

  16. Tian X, Zuo M, Fyfe KR (2004) Analysis of the vibration response of a gearbox with gear tooth faults. In: ASME international mechanical engineering congress and exposition, pp 785–793. ASME, Anaheim

  17. Sainsot P, Velex P, Duverger O (2004) Contribution of gear body to tooth deflections-a new bidimensional analytical formula. J Mech Des 126(4):748–752

    Article  Google Scholar 

  18. Tian X (2004) Dynamic simulation for system response of gearbox including localized gear faults. 2004. 109 f. Master’s thesis, University of Alberta

  19. Li Z, Zhu C, Liu H, Gu Z (2020) Mesh stiffness and nonlinear dynamic response of a spur gear pair considering tribo-dynamic effect. Mech Mach Theory 153:103989

    Article  Google Scholar 

  20. Dowson D, Higginson GR (1977) Elasto-hydrodynamic lubrication: international series on materials science and technology. Pergamon Press, New York

    Google Scholar 

  21. Zhang Y, Liu H, Zhu C, Song C (2017) Lubrication film stiffness of a spur gear pair. In: Proceedings of the international conference on power transmissions, London, pp 981–986

  22. Inman DJ (2014) Engineering Vibration, vol 4. Pearson Education, New Jersey, p 24

    Google Scholar 

  23. Rao SS (2011) Mechanical vibrations. Pearson Education, New Jersey, pp 158–164

    Google Scholar 

  24. Thomson WT (2018) Theory of vibration with applications, 4th edn. CrC Press, Santa Barbara

    Book  Google Scholar 

  25. Luo B, Li W (2017) Influence factors on bulk temperature field of gear. Proc Inst Mech Eng Part J J Eng Tribol 231(8):953–964

    Article  Google Scholar 

  26. Ribeiro AA, Karas EW (2001) Um curso de otimizaçao. Universidade de Curitiba, Curitiba, Brasil

  27. Sánchez MB, Pleguezuelos M, Pedrero JI (2017) Approximate equations for the meshing stiffness and the load sharing ratio of spur gears including hertzian effects. Mech Mach Theory 109:231–249

    Article  Google Scholar 

  28. Luo B, Li W (2019) Research on tooth profile modification based on system dynamic characteristics under thermoelastic coupling condition. Meccanica 54(10):1499–1513

    Article  MathSciNet  Google Scholar 

  29. Khabou M, Bouchaala N, Chaari F, Fakhfakh T, Haddar M (2011) Study of a spur gear dynamic behavior in transient regime. Mech Syst Signal Process 25(8):3089–3101

    Article  Google Scholar 

Download references

Acknowledgements

The authors of this research work wish to acknowledge Universidade Federal do Amazonas (UFAM) and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) for the resources and amenities provided during the implementation of this work.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001.

Author information

Author notes

  1. Gustavo C. Silva Neto, Danilo S. Chui have contributed equally to this work.

Authors and Affiliations

  1. Departamento de Engenharia Mecânica, Faculdade de Tecnologia da Universidade Federal do Amazonas (UFAM), Av. Rodrigo Otávio, 6200, Manaus, AM, 69080-900, Brazil

    Flávio H. A. S. Dias, Gustavo C. Silva Neto & Danilo S. Chui

Authors
  1. Flávio H. A. S. Dias
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gustavo C. Silva Neto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Danilo S. Chui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Danilo S. Chui.

Ethics declarations

Conflict of interest

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this paper.

Additional information

Technical Editor: Adriano Todorovic Fabro.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dias, F.H.A.S., Silva, G.C. & Chui, D.S. Vibration attenuation on spur gears through optimal profile modification based on an alternative dynamic model. J Braz. Soc. Mech. Sci. Eng. 46, 10 (2024). https://doi.org/10.1007/s40430-023-04574-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-023-04574-3

Keywords

Search

Navigation