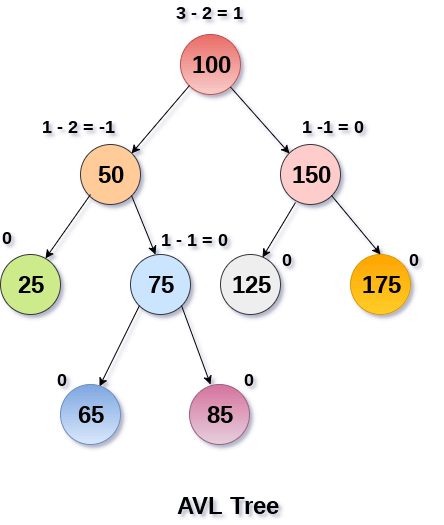
- AVL tree is a self-balancing binary search tree in which each node maintains extra information called a balance factor whose value is either -1, 0 or +1.
- Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of the right subtree of that node.
- Left rotation(L) : In left rotations, every node moves one position to left from the current position.
- Right rotation(R) : In right rotations, every node moves one position to right from the current position.
- Left Right rotation(LR) : In left right roation, First every node moves one position to the left, then one position to the right from the current position.
- Right Left rotaton(RL) : In right left rotation, First every node moves one position to the right, then one position to the left from the current position.
- Insert a new element into the tree using BST's (Binary Search Tree) insertion logic.
- After inserting the element check the Balance Factor of each node.
- When the balance factor of any node comes other than the three values(0,1,-1) then the tree is said to be unbalanced. Then perform the suitable Rotation to make it balanced.
- If there is an imbalance in the left child's right sub-tree, perform a left-right rotation
- If there is an imbalance in the left child's left sub-tree, perform a right rotation
- If there is an imbalance in the right child's right sub-tree, perform a left rotation
- If there is an imbalance in the right child's left sub-tree, perform a right-left rotation
- If the node to be deleted is a leaf node, it is simply removed from the tree.
- If the node to be deleted has one child node, the child node is replaced with the node to be deleted simply.
- If the node to be deleted has two child nodes then,
- Either replace the node with it’s inorder predecessor , i.e, the largest element of the left sub tree.
- Or replace the node with it’s inorder successor , i.e, the smallest element of the right sub tree.
- If the tree is unbalanced, then perform the suitable rotation to make it balanced.
- If there is an imbalance in the left child's right sub-tree, perform a left-right rotation
- If there is an imbalance in the left child's left sub-tree, perform a right rotation
- If there is an imbalance in the right child's right sub-tree, perform a left rotation
- If there is an imbalance in the right child's left sub-tree, perform a right-left rotation
- First compare the searching element with root, if less than root, then recursively call left subtree, else recursively call right subtree.
- If the element to search is found anywhere, return true, else return false.
- Time complexity
- insertion : O(logn)
- deletion : O(logn)
- search : O(logn)
- Space complexity : O(n)
- AVL tree has capabilities of self-balancing
- AVL trees have efficient search time complexity
- AVL trees are very difficult to implement
- A binary search tree follows some order to arrange the elements.
- In a Binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node.
- A height-balanced binary tree is defined as a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
- To check if a tree is height-balanced, get Get the Middle of the array and make it root.
- Get the middle of left half and make it left child of the root created in step 1.
- Get the middle of right half and make it right child of the root created in step 1.
- Return true if difference between heights is not more than 1 and left and right subtrees are balanced, otherwise return false.
- First, compare the element to be searched with the root element of the tree.
- If root is matched with the target element, then return the node's location.
- If it is not matched, then check whether the item is less than the root element, if it is smaller than the root element, then move to the left subtree.
- If it is larger than the root element, then move to the right subtree.
- Repeat the above procedure recursively until the match is found.
- If the element is not found or not present in the tree, then return NULL.
- Insertion :- O(n)
- Deletion :- O(n)
- Search :- O(n)
- Space Complexity :- O(n)
- Searching an element in the Binary search tree is easy as we always have a hint that which subtree has the desired element.
- As compared to array and linked lists, insertion and deletion operations are faster in BST.
- Many algorithms can be expressed more easily because it is just a binary tree.
- It employs recursive approach which requires more stack space.
- The interaction of binary search with memory hierarchy i.e. caching is poor.
- A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
- A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
- The left subtree of the binary search tree contains those values that are lesser than the node’s key. While performing this, it is not necessary that the tree should have an equal number of left nodes and right nodes.
- On the same lines, the next characteristic of the binary tree is that the right subtree contains values that are greater than the node’s key. Likewise, to the earlier point, while performing this, it is not necessary that the tree should have an equal number of right nodes and left nodes.
- Each of the subtrees that is formed should be a binary tree as a standalone, which essentially means that when we cut the full tree at any node, the resulting tree should be a binary search tree in itself.
- To convert bst from preoder traversal firstly we have to set a range {min .. max} for every node.
- Initialize the range as {INT_MIN .. INT_MAX}.
- The first node will definitely be in range, so create a root node. To construct the left subtree, set the range as {INT_MIN …root->data}.
- If a value is in the range {INT_MIN .. root->data}, the values are part of the left subtree.
- To construct the right subtree, set the range as {root->data..max .. INT_MAX}.
For Searching : time complexity is O(h) where h is height of BST.
For Insertion : time complexity is O(h) where h is height of BST.
For Deletion : deletion in binary tree has worst case complexity of O(n). In general, time complexity is O(h).
- We can always keep the cost of insert(), delete(), lookup() to O(logN) where N is the number of nodes in the tree so the benefit really is that lookups can be done in logarithmic time which matters a lot when N is large.
- We can implement order statistics with binary search tree - Nth smallest, Nth largest element. This is because it is possible to look at the data structure as a sorted array.
- BST can also be used in the design of memory allocators to speed up the search of free blocks, and to implement best fit algorithms where we are interested in finding the smallest free chunk with size greater than or equal to size specified in allocation request.
- We have an ordering of keys stored in the tree. Any time we need to traverse the increasing (or decreasing) order of keys, we just need to do the in-order (and reverse in-order) traversal on the tree.
- The main disadvantage is that we should always implement a balanced binary search tree. Otherwise the cost of operations may not be logarithmic and degenerate into a linear search on an array.
- The shape of the tree depends on the order of insertions, and it can be degenerated.
- When inserting or searching for an element, the key of each visited node has to be compared with the key of the element to be inserted/found. Keys may be long and the run time may increase much.