• About
• Status
• Related packages
• Installation
• Dependencies
• Usage examples
• API
• Authors
• License

Multivariate dual number algebra, automatic differentiation.

• Wikipedia: Dual numbers
• Wikipedia: Automatic_differentiation

(Package name with hat tip to @paniq)

Dual numbers are an elegant solution to compute precise⁽¹⁾ derivatives of functions which otherwise require complex & brittle numerical solutions. Furthermore, multivariate dual numbers can be used to obtain (in parallel) derivatives of multiple variables within a single function execution.

In this package, dual numbers are encoded as vanilla JS arrays with the internal structure: [real, d1 .. dn], where real is the real-valued part of the number and d1..dn multivariate derivatives. At minimum, at least d1 exists, but the number (of derivatives) depends on usage and the number of variables in a function one wishes to compute derivatives for.

⁽¹⁾ Here "precise" within the realm of IEEE-754

Some examples (see further below for code example):

[Math.PI, 0] // the scalar π as 1-dual number
[Math.PI, 1] // π as the current value of a 1-dual variable

[5, 1, 0] // 5 as first variable in 2-variable function
[3, 0, 1] // 3 as second variable in a 2-var function

[5, 1, 0, 0] // 1st var in 3-var fn
[3, 0, 1, 0] // 2nd var in 3-var fn
[2, 0, 0, 1] // 3rd var in 3-var fn

Alternatively, use convenience fns to create dual numbers:

$(5)     // [5, 0]
$(5, 1)  // [5, 1]

$2(5)    // [5, 0, 0]
$2(5, 2) // [5, 0, 1]

$3(5)    // [5, 0, 0, 0]
$3(5, 2) // [5, 0, 1, 0]

dual(5, 6)    // [5, 0, 0, 0, 0, 0, 0]
dual(5, 6, 4) // [5, 0, 0, 0, 1, 0, 0]

The following operations are available so far. Each operation takes one or more multivariate dual number(s) and computes the actual real-valued results as well as the 1st derivatives. Each op has an optimized/loop-free impl for 1-dual numbers.

• add(a, b)
• sub(a, b)
• mul(a, b)
• div(a, b)
• neg(a)
• abs(a)

Exponentials:

• pow(a, k) (k = scalar)
• sqrt(a)
• exp(a)
• log(a)

Trigonometry:

• sin(a)
• cos(a)
• tan(a)
• atan(a)

Polynomials:

• quadratic(x, a, b, c) ⇒ ax^2 + bx + c
• cubic(x, a, b, c, d) ⇒ ax^3 + bx^2 + cx + d
• quartic(x, a, b, c, d, e) ⇒ ax^4 + bx^3 + cx^2 + dx + e

For each polynomial, there're scalar versions available too, taking only rational numbers as arguments (rather than dual numbers already). These versions are suffixed with S (for "scalar"): quadraticS, cubicS and quarticS...

ALPHA - bleeding edge / work-in-progress

Search or submit any issues for this package

• @thi.ng/math - Assorted common math functions & utilities

yarn add @thi.ng/dual-algebra

ES module import:

<script type="module" src="https://cdn.skypack.dev/@thi.ng/dual-algebra"></script>

Skypack documentation

For Node.js REPL:

const dualAlgebra = await import("@thi.ng/dual-algebra");

Package sizes (brotli'd, pre-treeshake): ESM: 991 bytes

• @thi.ng/api

One project in this repo's /examples directory is using this package:

Screenshot	Description	Live demo	Source
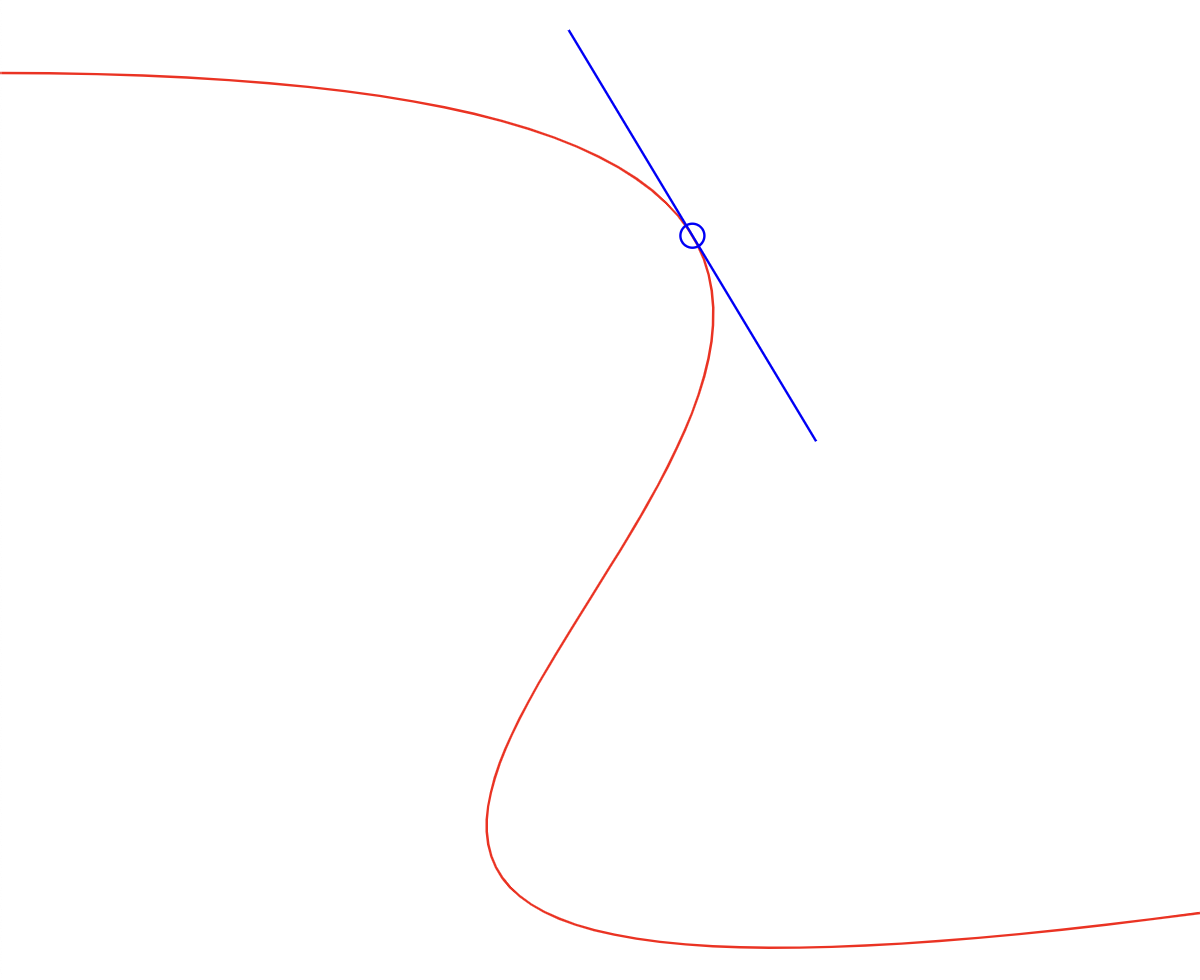	Compute cubic spline position & tangent using Dual Numbers	Demo	Source

Generated API docs

import { $2, add, mul, neg, sin, evalFn2 } from "@thi.ng/dual-algebra";

// compute the actual result and derivatives of X & Y
// of this function with 2 variables:
// z = -x^2 + 3 * sin(y)

const f = (x: number, y: number) => {
    // convert to multivariate dual numbers
    const xx = $2(x, 1);
    const yy = $2(y, 2);
    // compute...
    return add(neg(mul(xx, xx)), mul($2(3), sin(yy)));
}

// `evalFn2()` is higher order fn syntax sugar to simplify
// dealing w/ scalars, here same with that wrapper:
const g = evalFn2((x, y) => add(neg(mul(x, x)), mul($2(3), sin(y))));

f(0, 0);
// [0, 0, 3] => [f(x,y), dFdx(f(x,y)), dFdy(f(x,y))]

g(0, 0);
// [0, 0, 3]

f(1, Math.PI);
// [-0.9999999999999997, -2, -3]

Polynomial example (see interactive graph of this function):

import { add, mul, pow, cubicS } from "@thi.ng/dual-algebra";

// compute the cubic polynomial: f(x) = 2x^3 - 3x^2 - 4x + 5

// using `cubicS()` polynomial helper
const f1 = (x: number) => cubicS(x, 2, -3, -4, 5);

// ...or expanded out
const f2 = (x: number) =>
    add(
        add(
            add(
                mul([2, 0], pow([x, 1], 3)),
                mul([-3, 0], pow([x, 1], 2))
            ),
            mul([-4, 0], [x, 1])
        ),
        [5, 0]
    );

f2(0) // [5, -4] [f(x), dFdx(f(x))]
f2(1) // [0, -4]
f2(2) // [1, 8]

• Karsten Schmidt

If this project contributes to an academic publication, please cite it as:

@misc{thing-dual-algebra,
  title = "@thi.ng/dual-algebra",
  author = "Karsten Schmidt",
  note = "https://thi.ng/dual-algebra",
  year = 2020
}

© 2020 - 2024 Karsten Schmidt // Apache License 2.0