-
-
Notifications
You must be signed in to change notification settings - Fork 0
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
1 parent
c66c940
commit eb731de
Showing
5 changed files
with
40 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,5 @@ | ||
| --- | ||
| title: Geometric genus | ||
| --- | ||
|
|
||
| The *geometric genus* of a smooth connected curve $C$ is what one expects and can be defined in many ways, e.g. $\frac{1}{2}\dim H^1(C)$. For an irreducible, singular curve, the geometric genus is then defined to be the genus of its normalization (the curve obtained by ungluing all the nodes). |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,11 @@ | ||
| --- | ||
| title: Gromov-Witten invariants | ||
| --- | ||
|
|
||
| Gromov-Witten invariants count (in a loose sense only) holomorphic maps from genus 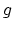 Riemann surfaces to a variety 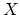 which pass through a given collection of cycles on 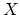. In order to define these, we compactify the space of maps from a variable pointed curve 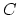 to 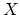 by allowing the domain curve to degenerate to a nodal curve so that the corresponding map always has finite automorphism group. For a fixed genus 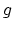, image homology class 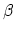, and number of marked points 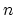, this gives the moduli space of stable maps 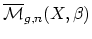 which is typically a highly singular Deligne-Mumford stack. The Gromov-Witten invariants of 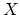 are given by integrals | ||
|
|
||
| ![$\displaystyle \int_{[\overline{\mathcal{M}}_{g,n}(X,\beta)]^\mathrm{vir}} | ||
| ev_1^*(\alpha_1) \cdots ev_n^*(\alpha_n) | ||
| $](https://www.aimath.org/WWN/modspacecurves/glossary/img70.png) | ||
|
|
||
| where 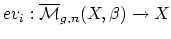 is evaluation at the 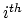 marked point and the 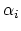 are elements of 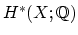. An important point of the theory is that this integral is defined via cap product with a distinguished homology class known as the virtual fundamental class of 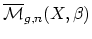. The descendent Gromov-Witten Invariants are obtained by inserting monomials in the Witten classes 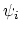 into the integral. |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,11 @@ | ||
| --- | ||
| title: Group completion | ||
| --- | ||
|
|
||
| Given a topological monoid $M$, the group completion is the space $\Omega BM$, where $BM$ is the classifying space of $M$ (thinking of $M$ as a topological category). If $M$ is already a topological group, then this operation does not change $M$ up to homotopy equivalence. Under some assumptions, we have the following description of the homology of the group completion. If we treat the monoid $\pi_{0}(M)$ as a directed system (with maps given by the monoid operation), then | ||
| $$ | ||
| \displaystyle \lim_{\alpha \in \pi_{0}(M)} H_{\ast}(M_{\alpha}) = H_{\ast}((\Omega | ||
| BM)_{0}) | ||
| $$ | ||
| in situations where the direct limit on the left-hand side is well-defined. In particular, if we consider the monoid $\amalg_g | ||
| B\Gamma_{g,2}$, the homology of the group completion is precisely the stable homology. The plus construction can often be used to give an alternative construction of the group completion. |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,7 @@ | ||
| --- | ||
| title: Harer stability | ||
| --- | ||
|
|
||
| Harer stability states that the degree 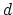 homology of the mapping class group 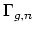 is independent of 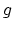 and 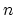 if 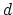 is small compared to 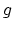. More precisely, consider the following maps on classifying spaces. First, we construct a map 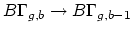 by adjoining a disk to a given boundary component. Second, we can construct a map 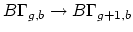 by gluing a torus with two boundary components along a given boundary component of our original Riemann surface. Harer's stability theorem asserts that both of these maps induce an isomorphism on 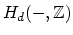 for 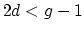. In particular, it allows us to talk about the stable homology/cohomology of the moduli space of curves, as in Mumford's conjecture. |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,6 @@ | ||
| --- | ||
| title: Spectrum | ||
| --- | ||
|
|
||
| A spectrum 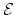 is (roughly) a sequence of based spaces 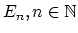, provided with maps 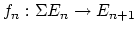 (where 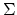 denotes suspension). There are many different definitions of the category of spectra, but they all yield the same homotopy category, known as the stable homotopy category. The homotopy category of spectra forms a triangulated category (with shifts given by suspension and looping); if we associate to a space 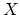 the suspesion spectrum 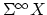 with 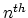-space 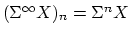, the homotopy classes of maps between the suspension spectra of 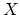 and 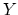 are the stable homotopy classes of maps between 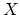 and 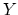. There is a correspondence between generalized (co)homology theories and spectra as follows. Given a generalized cohomology theory 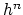, the Brown representability theorem gives a (universal) space 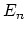 such that ![$ h^{n}(X) = [X,E_{n}]$](https://www.aimath.org/WWN/modspacecurves/glossary/img166.png); the suspension axiom provides the required structure maps for 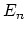 to form a spectrum. Conversely, for any spectrum 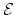, the functor ![$ h^n(X) = [X,\Omega^n \mathcal{E}]$](https://www.aimath.org/WWN/modspacecurves/glossary/img167.png) is a generalized cohomology theory, and 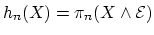 is a generalized homology theory. |