The Batch Normalization paper describes a method to address the various issues related to training of Deep Neural Networks. It makes normalization a part of the architecture itself and reports significant improvements in terms of the number of iterations required to train the network.
Covariate shift refers to the change in the input distribution to a learning system. In the case of deep networks, the input to each layer is affected by parameters in all the input layers. So even small changes to the network get amplified down the network. This leads to change in the input distribution to internal layers of the deep network and is known as internal covariate shift.
It is well established that networks converge faster if the inputs have been whitened (ie zero mean, unit variances) and are uncorrelated and internal covariate shift leads to just the opposite.
Saturating nonlinearities (like tanh or sigmoid) can not be used for deep networks as they tend to get stuck in the saturation region as the network grows deeper. Some ways around this are to use:
- Nonlinearities like ReLU which do not saturate
- Smaller learning rates
- Careful initializations
Let us say that the layer we want to normalize has d dimensions x = (x1, ... xd). Then, we can normalize the kth dimension as follows:
We also need to scale and shift the normalized values otherwise just normalizing a layer would limit the layer in terms of what it can represent. For example, if we normalize the inputs to a sigmoid function, then the output would be bound to the linear region only.
So the normalized input xk is transformed to:
where γ and β are parameters to be learned.
Moreover, just like we use mini-batch in Stochastic Gradient Descent (SGD), we can use mini-batch with normalization to estimate the mean and variance for each activation.
The transformation from x to y as described above is called Batch Normalizing Tranform. This BN transform is differentiable and ensures that as the model is training, the layers can learn on the input distributions that exhibit less internal covariate shift and can hence accelerate the training.
At training time, a subset of activations in specified and BN transform is applied to all of them.
During test time, the normalization is done using the population statistics instead of mini-batch statistics to ensure that the output deterministically depends on the input.
Let us say that x = g(Wu+b) is the operation performed by the layer where W and b are the parameters to be learned, g is a nonlinearity and u is the input from the previous layer.
The BN transform is added just before the nonlinearity, by normalizing x = Wu+b. An alternative would have been to normalize u itself but constraining just the first and the second moment would not eliminate the covariate shift from u.
When normalizing Wu+b, we can ignore the b term as it would be canceled during the normalization step (b's role is subsumed by β) and we have
z = g( BN(Wu) )
For convolutional layers, normalization should follow the convolution property as well - ie different elements of the same feature map, at different locations, are normalized in the same way. So all the activations in a mini-batch are jointly normalized over all the locations and parameters (γ and β) are learnt per feature map instead of per activation.
- Reduces internal covariant shift.
- Reduces the dependence of gradients on the scale of the parameters or their initial values.
- Regularizes the model and reduces the need for dropout, photometric distortions, local response normalization and other regularization techniques.
- Allows use of saturating nonlinearities and higher learning rates.
Batch Normalization was applied to models trained for MNIST and Inception Network for ImageNet. All the above-mentioned advantages were validated in the experiments. Interestingly, Batch Normalization with sigmoid achieved an accuracy of 69.8% (overall best, using any nonlinearity, was 74.8%) while Inception model (sigmoid nonlinearity), without Batch Normalisation, worked only as good as a random guess.
While BN Transform does enhance the overall deep network training task, its precise effect on gradient propagation is still not well understood. A future extension of Batch Normalisation would be in the domain of Recurrent Neural Networks where internal covariate shift and vanishing gradients are more severe. It remains to be explored if it can also help with domain adaption by easily generalizing to new data distributions.
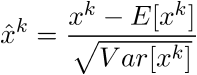
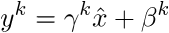
Hello @shagunsodhani, may I ask a question about this paper here?
In the section 2 of this paper, there's an example says that if
I've got author's point. However, how can I derive the correct gradient for bias b in above example?
It seems that the last equation in the example u + (b + delta_b) - E[u + (b + delta_b)] = u + b - E[u + b] can always be established no matter what delta_b is.