Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Travelling waves and spatial hierarchies in measles epidemics

Nature volume 414, pages 716–723 (2001)Cite this article

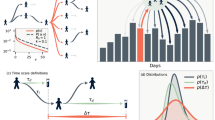
Abstract

Spatio-temporal travelling waves are striking manifestations of predator–prey and host–parasite dynamics. However, few systems are well enough documented both to detect repeated waves and to explain their interaction with spatio-temporal variations in population structure and demography. Here, we demonstrate recurrent epidemic travelling waves in an exhaustive spatio-temporal data set for measles in England and Wales. We use wavelet phase analysis, which allows for dynamical non-stationarity—a complication in interpreting spatio-temporal patterns in these and many other ecological time series. In the pre-vaccination era, conspicuous hierarchical waves of infection moved regionally from large cities to small towns; the introduction of measles vaccination restricted but did not eliminate this hierarchical contagion. A mechanistic stochastic model suggests a dynamical explanation for the waves—spread via infective ‘sparks’ from large ‘core’ cities to smaller ‘satellite’ towns. Thus, the spatial hierarchy of host population structure is a prerequisite for these infection waves.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Wavelet time series analysis for the log-transformed weekly London measles time series (see Box 1 for details).
Figure 2: Wavelet phase analysis of weekly measles reports for Cambridge, Norwich and London in the pre-vaccine era.
Figure 3: Phase differences from London for the full urban data set (954 locations).
Figure 4: Pre-vaccination (black) and vaccine era (red).
Figure 5: Average biennial behaviour of a spatially coupled measles model (see Box 2 for details).

Similar content being viewed by others

References

  1. Murray, J. D. Mathematical Biology (Springer, London, 1989).

    MATH  Google Scholar 

  2. Neubert, M. G., Kot, M. & Lewis, M. A. Dispersal and pattern formation in a discrete-time predator–prey model. Theor. Pop. Biol. 48, 7–43 (1995).

    MATH  Google Scholar 

  3. Sherratt, J. A. Periodic travelling waves in cyclic predator–prey systems. Ecol. Lett. 4, 30–37 (2001).

    Google Scholar 

  4. Hassell, M. P., Comins, H. N. & May, R. M. Spatial structure and chaos in insect population dynamics. Nature 353, 255–258 (1991).

    ADS  Google Scholar 

  5. Sole, R. V., Valls, J. & Bascompte, J. Spiral waves, chaos and multiple attractors in lattice models of interacting populations. Phys. Lett. A 166, 123–128 (1992).

    ADS  Google Scholar 

  6. Jeltsch, F., Muller, M. S., Grimm, V., Wissel, C. & Brandl, R. Pattern formation triggered by rare events: Lessons from the spread of rabies. Proc. R. Soc. Lond. B 264, 495–503 (1997).

    ADS  CAS  Google Scholar 

  7. Bjørnstad, O. N., Ims, R. A. & Lambin, X. Spatial population dynamics: analysing patterns and processes of population synchrony. Trends Ecol. Evol. 14, 427–432 (1999).

    PubMed  Google Scholar 

  8. Blasius, B., Huppert, A. & Stone, L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 399, 354–359 (1999).

    ADS  CAS  PubMed  Google Scholar 

  9. Mollison, D. Modeling biological invasions—chance, explanation, prediction. Phil. Trans. R. Soc. Lond. B 314, 675–693 (1986).

    ADS  Google Scholar 

  10. Bulmer, M. G. A statistical analysis of the 10-year cycle in Canada. J. Anim. Ecol. 43, 701–718 (1974).

    Google Scholar 

  11. Lambin, X., Elston, D. A., Petty, S. J. & MacKinnon, J. L. Spatial asynchrony and periodic travelling waves in cyclic populations of field voles. Proc. R. Soc. Lond. B 265, 1491–1496 (1998).

    CAS  Google Scholar 

  12. Ranta, E. & Kaitala, V. Travelling waves in vole population dynamics. Nature 390, 456–456 (1997).

    ADS  Google Scholar 

  13. Stenseth, N. C. et al. Common dynamic structure of Canada lynx populations within three climatic regions. Science 285, 1071–1073 (1999).

    CAS  PubMed  Google Scholar 

  14. Cliff, A. D., Haggett, P. & Smallman-Raynor, M. Measles: An Historical Geography of a Major Human Viral Disease from Global Expansion to Local Retreat, 1840–1990 (Blackwell, Oxford, 1993).

    Google Scholar 

  15. Grenfell, B. T. & Bolker, B. M. Cities and villages: infection hierarchies in a measles metapopulation. Ecol. Lett. 1, 63–70 (1998).

    Google Scholar 

  16. Bartlett, M. S. in Proc. Third Berkeley Symp. on Mathematical Statistics and Probability Vol. 4, 81–109 (Univ. California Press, Berkeley, 1956).

    Google Scholar 

  17. Schenzle, D. An age-structured model of pre- and post-vaccination measles transmission. IMA J. Math. Appl. Med. Biol. 1, 169–191 (1984).

    MathSciNet  CAS  PubMed  MATH  Google Scholar 

  18. Anderson, R. M. & May, R. M. Infectious Diseases of Humans: Dynamics and Control (Oxford Univ. Press, Oxford, 1991).

    Google Scholar 

  19. Grenfell, B. T. & Harwood, J. (Meta)population dynamics of infectious diseases. Trends Ecol. Evol. 12, 395–399 (1997).

    CAS  PubMed  Google Scholar 

  20. Earn, D. J. D., Rohani, P., Bolker, B. M. & Grenfell, B. T. A simple model for complex dynamical transitions in epidemics. Science 287, 667–670 (2000).

    ADS  CAS  PubMed  Google Scholar 

  21. Finkenstädt, B. F. & Grenfell, B. T. Time series modelling of childhood diseases: a dynamical systems approach. J. R. Stat. Soc. C 49, 187–205 (2000).

    MathSciNet  MATH  Google Scholar 

  22. Grenfell, B. T., Bjornstad, O. N. & Finkenstädt, B. F. Dynamics of measles epidemics. II. Scaling noise, determinism and predictability with the time series SIR model. Ecol. Monogr. (in the press).

  23. Torrence, C. & Compo, G. P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78 (1998).

    ADS  Google Scholar 

  24. Nason, G. P. & von Sachs, R. Wavelets in time series analysis. Phil. Trans. R. Soc. Lond. A 357, 2511–2526 (1999).

    ADS  MathSciNet  MATH  Google Scholar 

  25. Daubechies, I. Ten Lectures on Wavelets (Society for Industrial and Applied Mathematics, Philadelphia, 1992).

    MATH  Google Scholar 

  26. Percival, D. B. & Walden, A. T. Wavelet Methods for Time Series Analysis (Cambridge Univ. Press, Cambridge, 2000).

    MATH  Google Scholar 

  27. Bartlett, M. S. Measles periodicity and community size. J. R. Stat. Soc. A 120, 48–70 (1957).

    Google Scholar 

  28. Anderson, R. M., Grenfell, B. T. & May, R. M. Oscillatory fluctuations in the incidence of infectious disease and the impact of vaccination: time series analysis. J. Hyg. 93, 587–608 (1984).

    CAS  PubMed  PubMed Central  Google Scholar 

  29. Chatfield, C. The Analysis of Time Series: An Introduction (Chapman and Hall, London, 1996).

    MATH  Google Scholar 

  30. Finkenstädt, B. F. & Grenfell, B. T. Empirical determinants of measles metapopulation dynamics in England and Wales. Proc. R. Soc. Lond. B 265, 211–220 (1998).

    Google Scholar 

  31. Lloyd, A. L. & May, R. M. Spatial heterogeneity in epidemic models. J. Theor. Biol. 179, 1–11 (1996).

    ADS  CAS  PubMed  Google Scholar 

  32. Earn, D., Rohani, P. & Grenfell, B. T. Spatial dynamics and persistence in ecology and epidemiology. Proc. R. Soc. Lond. B 265, 7–10 (1998).

    CAS  Google Scholar 

  33. Bolker, B. M. & Grenfell, B. T. Impact of vaccination on the spatial correlation and dynamics of measles epidemics. Proc. Natl Acad. Sci. USA 93, 12648–12653 (1996).

    ADS  CAS  PubMed  PubMed Central  Google Scholar 

  34. Cliff, A. D., Haggett, P., Stroup, D. F. & Cheney, E. The changing geographical coherence of measles morbidity in the United States, 1962–88. Stat. Med. 11, 1409–1424 (1992).

    CAS  PubMed  Google Scholar 

  35. Bartless, M. S. The critical community size for measles in the U.S. J. R. Stat. Soc. A 123, 37–44 (1960).

    Google Scholar 

  36. Grenfell, B. T., Bolker, B. M. & Kleczkowski, A. Seasonality and extinction in chaotic metapopulations. Proc. R. Soc. Lond. B 259, 97–103 (1995).

    ADS  MATH  Google Scholar 

  37. Kendall, B. E., Schaffer, W. M. & Tidd, C. W. Transient periodicity in chaos. Phys. Lett. A 177, 13–20 (1993).

    ADS  MathSciNet  Google Scholar 

  38. Bradshaw, G. A. & Spies, T. A. Characterizing canopy gap structure in forests using wavelet analysis. J. Ecol. 80, 205–215 (1992).

    Google Scholar 

  39. Bjørnstad, O. N. & Bascompte, J. Synchrony and second order spatial correlation in host-parasitoid systems. J. Anim. Ecol. 70, 924–933 (2001).

    Google Scholar 

  40. Schaffer, W. M. & Kot, M. Nearly one dimensional dynamics in an epidemic. J. Theor. Biol. 112, 403–427 (1985).

    ADS  MathSciNet  CAS  PubMed  Google Scholar 

  41. Schwartz, I. B. in Biomedical Modelling and Simulation (eds Eisenfeld, J. & Levine, D. S.) 201–204 (Scientific, New York, 1989).

    Google Scholar 

  42. Bolker, B. M. & Grenfell, B. T. Space, persistence and the dynamics of measles epidemics. Phil. Trans. R. Soc. Lond. B 348, 309–320 (1995).

    ADS  CAS  Google Scholar 

  43. Hanski, I. & Gyllenberg, M. Two general metapopulation models and the core-satellite hypothesis. Am. Nat. 142, 17–41 (1993).

    Google Scholar 

  44. Bak, P. How Nature Works—The Science of Organised Criticality (Oxford Univ. Press, Oxford, 1977).

    Google Scholar 

  45. Rhodes, C. J. & Anderson, R. M. Power laws governing epidemics in isolated populations. Nature 381, 600–602 (1996).

    ADS  CAS  PubMed  Google Scholar 

  46. Office of Population Censuses and Surveys Registrar General's Weekly Return for England and Wales (Her Majesty's Stationery Office (HMSO), London, 1944–94).

    Google Scholar 

  47. Hall, P. & Patil, P. Properties of nonparametric estimators of autocovariance for stationary random fields. Prob. Theor. Relat. Fields 99, 399–424 (1994).

    MathSciNet  MATH  Google Scholar 

  48. Bjørnstad, O. N. & Falck, W. Nonparametric spatial covariance functions: estimation and testing. Environ. Ecol. Stat. 8, 53–70 (2001).

    MathSciNet  Google Scholar 

  49. Bjørnstad, O. N., Finkenstädt, B. & Grenfell, B. T. Dynamics of measles epidemics. I. Estimating scaling of transmission rates using a time series SIR model. Ecol. Monogr. (in the press).

  50. May, R. M. & Anderson, R. M. Spatial heterogeneity and the design of immunization programs. Math. Biosci. 72, 83–111 (1984).

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank S. Cornell, T. Coulson, J. Gog, M. Keeling, A. Lloyd, G. Nason, P. Rohani, C. Torrence and C. Williams for helpful discussions. B.T.G. and J.K. were supported by the Wellcome Trust. O.N.B. was supported by the National Center for Ecological Analysis and Synthesis (a Centre funded by an NSF grant, the University of California Santa Barbara, and the State of California) and the Norwegian Science Foundation.

Author information

Authors and Affiliations

  1. Zoology Department, University of Cambridge, Downing Street, Cambridge, CB2 3EJ, UK

    B. T. Grenfell, O. N. Bjørnstad & J. Kappey

  2. Departments of Entomology and Biology, 501 ASI Building, Penn State University, University Park, 16802, Pennsylvania, USA

    O. N. Bjørnstad

Authors
  1. B. T. Grenfell
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. N. Bjørnstad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. Kappey
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. T. Grenfell.

Supplementary information

Figure I

(GIF 9.32 KB)

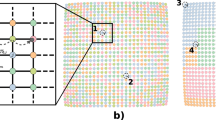
The figure (which accompanies Box 2, figure a) shows the mean (+/s.e.) biennial wavelet phase of 60 simulations of the spatial TSIR model with small centres, defined in Box 2 of the paper. To explore the phase relationships arising from approximately phase-locked biennial cycles, the simulations were run for 10 years, starting from the phase-locked deterministic attractor of the system.

Notes

  1. 1.

    The phase lag is not an ‘edge’ effect, since wrapped boundary condition also generate a phase lag near the city.

  2. 2.

    As we move away from the city, note that the phase error bars widen. This is partly due to greater irregularity nearer the edge, but also partly because occasional simulations drop onto the opposite attractor (with 180o phase lag). As noted in Box 2, this partly reflects distance from the city, but also a genuine edge effect (note that Norwich and its environs are near the coast, hence an ‘edge’ in terms of measles transmission).

  3. 3.

    Previous work (Bjørnstad et al. 2001, op. cit.) shows that the relative measles transmission rate (Ro) in the England and Wales data set is constant across 3 orders of magnitude of population size. In fact, the crude models used here show slight increases in transmission rate with coupling (because tight coupling in the crude way we have defined it can increase Ro).

    This is illustrated in Figure (II), which presents a phase analysis of the case when large centres are coupled (cf Box 2, figure (b) in the paper). Increased coupling between boroughs increases their effective Ro and causes them to lead the ‘periphery’ slightly, by 1 time step (2 weeks) – note also that the phase analysis picks up this small phase lag more sensitively than the crude plot of average biennia in Box 2.

    This effect – which is a byproduct of our coupling model, cannot cause the progressive phase lag of the periphery seen in Figure (I); this latter is driven by ‘sparks’ of infection in the hierarchical system, as described in Box 2. However, the effect of coupling on effective transmission does complicate the analysis of the relationship between waves and coupling. We are currently exploring this issue: preliminary analyses indicate that hierarchical waves will occur at a range of ‘intermediate coupling rates, as long as the overall dynamics are biennial and major epidemics occur in the same year. Recent work (1) indicates that a more mechanistic representation of coupling can remove the spurious slight increase in R0 in tightly-coupled centres.

    (1) Keeling, M.J. & Rohani, P. (2001) Spatial Coupling in Epidemiology: A Mechanistic Approach. Ecol. Letts. (in press).

Movie (FLI, 5.5 MB)

Structure of the movie frame

The movie shows the dynamics of measles in England and Wales during the period 1955-1965. The data are from the Registrar General's weekly notifications of measles in 954 urban locations; the movie plots a frame every 2 weeks.

The upper left quadrant shows observed measles dynamics, using colour coding for the logarithm of the number of reported infected cases (all data are scaled on (0-1) before plotting). Zero case reports are shown as white circles and circle size is proportional to {population size}0.2. The movie captures the overall synchonised biennial 'pulse' of measles epidemics, superimposed on the seasonal swing of infection. There are also more irregular epidemics in smaller places and many other interesting patterns, for example distinctive behaviour in many coastal towns.

The observed data also show travelling waves of measles, moving away from large centres such as London. These are revealed more clearly in the upper right quadrant, which shows the smoothed major epidemic cycles, filtered using wavelets in a window of 1.75 to 3 years. As discussed in the paper, the filtered series reveal dramatic waves of measles, moving away from large centres, especially London and the North West conurbation. The lower left quadrant shows the phase difference from London of these filtered series (see the paper for more details). The arrows and the colour of the arrows are indicators of the phase difference, as shown on the circular key (green denotes a zero phase difference from London, blue denotes a lag and yellow a lead). These give a more stable picture of the phase relationships -- notably, the wave moving away from London and a relatively early wave from the North West. Finally, the lower right quadrant plots a moving time bar against the London and Manchester series.

Running the movie after download

The format of the movie is flic, because it allows for high compression of the data. You can watch the movie in a variety of players - for example, Quicktime or the freeware Autodesk player AAwin.

Click here to download the Quicktime plugin >>> http://www.apple.com/quicktime/download/

Rights and permissions

Reprints and permissions

About this article

Cite this article

Grenfell, B., Bjørnstad, O. & Kappey, J. Travelling waves and spatial hierarchies in measles epidemics. Nature 414, 716–723 (2001). https://doi.org/10.1038/414716a

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/414716a

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing