Skip to main content
Springer Nature Link
Log in

Development of three-dimensional integral-type reconstruction formula for magnetic resonance elastography

  • Original Article
  • Published:
International Journal of Computer Assisted Radiology and Surgery Aims and scope Submit manuscript

Abstract

Purpose

The viscoelasticity (storage modulus and loss modulus) of living tissues is known to be related to diseases. Magnetic resonance elastography (MRE) is a quantitative method for non-invasive measuring viscoelasticity. The viscoelasticity is calculated from the elastic wave images using an inversion algorithm. The estimation accuracy of the inversion algorithm is degraded by background noise. This study aims to propose novel inversion algorithms that are applicable for noisy elastic wave images.

Methods

The proposed algorithms are based on the Voigt-type viscoelastic equation. The algorithms are designed to improve the noise robustness by avoiding direct differentiation of measurement data by virtue of Green's formula. Similarly, stabilization is introduced to the curl-operator which works to eliminate the compression waves in measurement data. To clarify the characteristics of the algorithms, the proposed algorithms were compared with the conventional algorithms using isotropic and anisotropic voxel numerical simulations and phantom experimental data.

Results

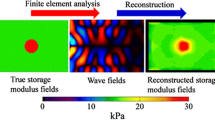
From the results of the numerical simulations, normalized errors of stiffness of proposed algorithms were 3% or less. The proposed algorithms mostly showed better results than the conventional algorithms despite noisy elastic wave images. From the gel phantom experiment, we confirmed the same tendency as the characteristics of the algorithms observed in the numerical simulation results.

Conclusion

We have developed a novel inversion algorithm and evaluated it quantitatively. The results confirm that the proposed algorithms are highly quantitative and noise-robust methods for estimating storage and loss modulus regardless of noise, voxel anisotropy, and propagation direction. Therefore, the proposed algorithms will appropriate to various three-dimensional MRE systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Canada)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Muthpillai R, Lomas DJ, Rossman PF, Greenleaf JF, Manduca A, Ehman RL (2020) Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science 269:1854–1857. https://doi.org/10.1126/science.7569924

    Article  Google Scholar 

  2. Liang Y, Li D (2020) Magnetic resonance elastography in staging liver fibrosis in non-alcoholic fatty liver disease: a pooled analysis of the diagnostic accuracy. BMC Gastroenterol 20(1):89. https://doi.org/10.1186/s12876-020-01234-x

    Article  PubMed  PubMed Central  Google Scholar 

  3. Singh S, Venkatesh SK, Loomba R, Wang Z, Sirlin C, Chen J, Yin M, Miller FH, Low RN, Hassanein T, Godfrey EM, Asbach P, Murad MH, Lomas DJ, Talwalkar JA, Ehman RL (2016) Magnetic resonance elastography for staging liver fibrosis in non-alcoholic fatty liver disease: a diagnostic accuracy systematic review and individual participant data pooled analysis. Eur Radiol 26(5):1431–1440. https://doi.org/10.1007/s00330-015-3949-z

    Article  PubMed  Google Scholar 

  4. Yin M, Talwalker JA, Glaser KJ, Manduca A, Grimm RC, Rossman PJ, Fidler JL, Ehman RL (2007) Assessment of hepatic fibrosis with magnetic resonance elastography. Clin Gastroenterol Hepatol 5(10):1207–1213. https://doi.org/10.1016/j.cgh.2007.06.012

    Article  PubMed  PubMed Central  Google Scholar 

  5. Yoon JH, Lee JM, Joo I, Lee ES, Sohn JY, Jang SK, Lee KB, Han JK, Choi BI (2014) Hepatic fibrosis: prospective comparison of MR elastography and US shear-wave elastography for evaluation. Radiology 273(3):772–782. https://doi.org/10.1148/radiol.14132000

    Article  PubMed  Google Scholar 

  6. Yoshimitsu K, Mitsufuji T, Shinagawa Y, Fujimitsu R, Morita A, Urakawa H, Hayashi H, Takano K (2016) MR Elastography of the liver at 3.0T in diagnosing liver fibrosis grades; preliminary clinical experience. Eur Radiol 26(3):656–663. https://doi.org/10.1007/s00330-015-3863-4

    Article  PubMed  Google Scholar 

  7. Thompson SM, Wang J, Chandan VS, Glaser KJ, Roberts LR, Ehman RL, Venkatesh SK (2017) MR elastography of hepatocellular carcinoma: correlation of tumor stiffness with histopathology features-Preliminary findings. Magn Reson Imaging 37:41–45. https://doi.org/10.1016/j.mri.2016.11.005

    Article  PubMed  Google Scholar 

  8. Li J, Zormpas-Petridis K, Boult JKR, Reeves EL, Heindl A, Vinci M, Lopes F, Cummings C, Springer CJ, Chesler L, Jones C, Bamber JC, Yuan Y, Sinkus R, Jamin Y, Robinson SP (2019) Investigating the contribution of collagen to the tumor biomechanical phenotype with noninvasive magnetic resonance elastography. Cancer Res 79(22):5874–5883. https://doi.org/10.1158/0008-5472.CAN-19-1595

    Article  CAS  PubMed  Google Scholar 

  9. Hiscox LV, Johnson CL, Barnhill E, McGarry MDJ, Huston J, van Beek EJR, Starr JM, Roberts N (2016) Magnetic resonance elastography (MRE) of the human brain: technique, findings and clinical applications. Phys Med Biol 61(24):R401–R437. https://doi.org/10.1088/0031-9155/61/24/R401

    Article  PubMed  Google Scholar 

  10. Murphy MC, Huston J 3rd, Ehman RL (2019) MR elastography of the brain and its application in neurological diseases. Neuroimage 187:176–183. https://doi.org/10.1016/j.neuroimage.2017.10.008

    Article  PubMed  Google Scholar 

  11. Garteiser P, Doblas S, Daire J, Wagner M, Leitao H, Vilgrain V, Sinkus R, Beers BEV (2012) MR elastography of liver tumours: value of viscoelastic properties for tumour characterization. Eur Radiol 22(10):2169–2177. https://doi.org/10.1007/s00330-012-2474-6

    Article  PubMed  Google Scholar 

  12. Pagé G, Tardieu M, Gennisson J, Besret L, Garteiser P, Beers BEV (2021) Tumor solid stress: assessment with MR elastography under compression of patient-derived hepatocellular carcinomas and cholangiocarcinomas xenografted in mice. Cancers 13(8):1891. https://doi.org/10.3390/cancers13081891

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  13. Knutsson H, Westin CF, Granlund G (1994) Local multiscale frequency and bandwidth estimation. Proc IEEE Int Conf Image Process 1:36–40

    Article  Google Scholar 

  14. Manduca A, Muthupillai R, Rossman P, Greenleaf JF, Ehman RL (1996) Local wavelength estimation for magnetic resonance elastography. Proc IEEE Int Conf Image Process 3:527–530

    Article  Google Scholar 

  15. Oliphant TE, Manduca A, Ehman RL, Greenleaf JF (2001) Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation. Magnet Resonance Med 45:299–310. https://doi.org/10.1002/1522-2594(200102)45:2%3c299::aid-mrm1039%3e3.0.co;2-o

    Article  CAS  Google Scholar 

  16. Romano AJ, Shirron JJ, Bucaro JA (1998) On the noninvasive determination of material parameters from a knowledge of elastic displacements theory and numerical simulation. IEEE Trans Ultrason Ferroelectr Freq Control 45:751–759. https://doi.org/10.1109/58.677725

    Article  CAS  PubMed  Google Scholar 

  17. Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, Felmlee JP, Greenleaf JF, Ehman RL (2001) Magnetic resonance elastography: non-invasive mapping of tissue elasticity. Med Image Anal 5(4):37–254. https://doi.org/10.1016/s1361-8415(00)00039-6

    Article  Google Scholar 

  18. Yin M, Talwalkar JA, Glaser KJ, Venkatesh SK, Chen J, Manduca A, Ehman RL (2011) Dynamic postprandial hepatic stiffness augmentation assessed with MR elastography in patients with chronic liver disease. Am J Roentgenol 197(1):64–70. https://doi.org/10.2214/AJR.10.5989

    Article  Google Scholar 

  19. Yasar TK, Wagner M, Bane O, Besa C, Babb JS, Kannengiesser S, Fung M, Ehman RL, Taouli B (2016) Inter-platform reproducibility of liver and spleen stiffness measured with MR elastography. J Magn Reson Imaging 43(5):1064–1072. https://doi.org/10.1002/jmri.25077

    Article  PubMed  Google Scholar 

  20. Silva AM, Grimm RC, Glazer KJ, Fu Y, Wu T, Ehman RL, Silva AC (2015) Magnetic resonance elastography: evaluation of new inversion algorithm and quantitative analysis method. Abdom Imaging 40(4):810–817. https://doi.org/10.1007/s00261-015-0372-5

    Article  PubMed  Google Scholar 

  21. Murphy MC, Manduca A, Trzasko JD, Glaser KJ, Huston J 3rd, Ehman RL (2018) Artificial neural networks for stiffness estimation in magnetic resonance elastography. Magn Reson Med 80(1):351–360. https://doi.org/10.1002/mrm.27019

    Article  PubMed  Google Scholar 

  22. Jiang Y, Fujiwara H, Nakamura G (2011) Approximate steady state models for magnetic resonance elastography. SIAM J Appl Math 71(6):1965–1989. https://doi.org/10.1137/100781882

    Article  Google Scholar 

  23. Sinkus R, Tanter M, Xydeas T, Catheline S, Bercoff J, Fink M (2005) Viscoelastic shear properties of in vivo breast lesions measured by MR elastography. Magn Reson Imaging 23(2):159–165. https://doi.org/10.1016/j.mri.2004.11.060

    Article  PubMed  Google Scholar 

  24. Mariappan YK, Glaser KJ, Ehman RL (2010) Magnetic resonance elastography: a review. Clin Anat 23(5):497–511. https://doi.org/10.1002/ca.21006

    Article  PubMed  PubMed Central  Google Scholar 

  25. Gill HE, Lisanti CJ, Schwope RB, Kim J, Katz M, Harrison S (2020) Technical success rate of MR elastography in a population without known liver disease. Abdom Radiol 46(2):590–596. https://doi.org/10.1007/s00261-020-02652-x

    Article  Google Scholar 

Download references

Acknowledgements

The work was supported in part by JSPS KAKENHI JP17H02115 and JP20H01821.

Author information

Authors and Affiliations

  1. Graduate School of Science and Engineering, Chiba University, 1-33 Yayoicho, Inage, Chiba, Chiba, 263-8522, Japan

    Tasuku Takeda & Mikio Suga

  2. Graduate School of Informatics, Kyoto University, Kyoto, Japan

    Hiroshi Fujiwara

  3. Center for Frontier Medical Engineering, Chiba University, Chiba, Japan

    Mikio Suga

Authors
  1. Tasuku Takeda
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hiroshi Fujiwara
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mikio Suga
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tasuku Takeda.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors.

Informed consent

This articles does not contain patient data.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Takeda, T., Fujiwara, H. & Suga, M. Development of three-dimensional integral-type reconstruction formula for magnetic resonance elastography. Int J CARS 16, 1947–1956 (2021). https://doi.org/10.1007/s11548-021-02517-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11548-021-02517-8

Keywords

Search

Navigation