Abstract
In order to understand how Wuhan curbed the COVID-19 outbreak in 2020, we build a network transmission model of 123 dimensions incorporating the impact of quarantine and medical resources as well as household transmission. Using our new model, the final infection size of Wuhan is predicted to be 50,662 (95%CI: 46,234, 55,493), and the epidemic would last until April 25 (95%CI: April 23, April 29), which are consistent with the actual situation. It is shown that quarantining close contacts greatly reduces the final size and shorten the epidemic duration. The opening of Fangcang shelter hospitals reduces the final size by about 17,000. Had the number of hospital beds been sufficient when the lockdown started, the number of deaths would have been reduced by at least 54.26%. We also investigate the distribution of infectious individuals in unquarantined households of different sizes. The high-risk households are those with size from two to four before the peak time, while the households with only one member have the highest risk after the peak time. Our findings provide a reference for the prevention, mitigation and control of COVID-19 in other cities of the world.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In early December 2019, an outbreak of the coronavirus disease 2019 (COVID-19) was reported in Wuhan, China. In Wuhan, which is an important transportation hub in China, tens of thousands of passengers were transported every day during the Spring Festival travel rush, which rapidly made COVID-19 an epidemic in the megacity. Also, as of January 22, 2020, 28 provinces, municipalities and autonomous regions of mainland China had reported confirmed cases.Footnote 1 In order to prevent further spread of the virus, Wuhan government decided a lockdown of the city on January 23, 2020,Footnote 2 and strictly controlled personnel entering into and leaving from the city. Then, a series of measures were taken for mitigating and stopping the transmission of COVID-19. All public transportation, including buses, subways, ships and passenger traffic, were suspended, and public places like entertainment venues and restaurants were closed. Community, villages and streets were also closed to minimize and stop the mobility of population.
At the same time, one-household one-pass card system was implemented in the city, and all entry and exit personnel were strictly registered. Moreover, the reopening of work places and schools was postponed. As of April 26, 2020, the number of new confirmed local cases in Wuhan had dropped to zero.Footnote 3
Though the COVID-19 epidemic in Wuhan City was curbed in last April, the global COVID-19 epidemic remains critical, with a total of more than 279 million confirmed cases and 5,399,598 deaths.Footnote 4 Therefore, it is of great importance to understand how Wuhan stopped the endemic, which will provide a valuable reference for mitigating and controlling the COVID-19 in the world.
The COVID-19 is transmitted mainly through close contact and respiratory droplets, with possible airborne transmission if aerosols are present (Chan et al. 2020; Huang et al. 2020). Symptoms include cough, fever and difficulty breathing, as with SARS (severe acute respiratory syndrome coronavirus) and MERS (Middle East respiratory syndrome coronavirus) (Wu et al. 2020a). The incubation period for COVID-19 is on average of 5–6 days, although it can take up to 14 days.Footnote 5 During this “pre-symptomatic” period, some infected individuals can be contagious; therefore, transmission from pre-symptomatic cases can occur before symptom onset.
During COVID-19 in Wuhan, the spreading epidemics were complicated. The lockdown of Wuhan effectively blocked the spatial spread of the COVID-19 and bought time for the prevention and control of the epidemic in China and other countries around the world (Chinazzi et al. 2020; Wells et al. 2020). However, for Wuhan, because the COVID-19 was an emerging infectious disease, human had little knowledge of COVID-19 and medical resources were not well ready yet. The lack of outpatient medical resources, such as test kits and medical personnel, makes it impossible for all infectious individuals to be timely tested and confirmed, which leads to a longer diagnosis time. The limited number of hospital beds makes it impossible to timely admit and cure all symptomatic infectious individuals, which leads to the prolonged transmission time of the infectious individuals. The lack of centrally quarantined points prevents close contacts from being quarantined in a timely and effective manner, which also leads to the increase in the risk of transmission. In order to overcome the shortage of medical personnel and materials in Wuhan, all other provinces successively sent essential healthcare personnel and medical resources to support Wuhan City in batches.
As an important medical resource, the number of hospital beds is directly related to the isolation and treatment of symptomatic infectious individuals. The more sufficient the number of hospital beds is, the more infectious individuals will be effectively isolated, and the transmission between people will be correspondingly reduced. Therefore, it is of great significance to study the emerging infectious diseases incorporated by the number of hospital beds. For the shortage of hospital beds, Wuhan had been increasing the number of designated hospitals (DHs) and began to build the Huoshenshan Hospital and Leishenshan Hospital on January 23, 2020, and January 25, 2020, respectively, immediately after the lockdown. Moreover, Fangcang Shelter Hospitals (FSHs) have been rapidly established and put into use since February 5, 2020, to treat patients with mild illnesses (Chen et al. 2020).Footnote 6
These measures have provided the most important material basis for the epidemic control in Wuhan. On the other hand, in the absence of an effective vaccine, quarantining close contacts is the most effective method in the prevention and control of emerging infectious diseases. To this end, while building hospitals, Wuhan had been increasing the number of centrally quarantined points. On the premise that there are vacant beds, every confirmed infectious individual is immediately hospitalized for massive isolation. At the same time, their close contacts are checked according to their social networks and are quarantined at home, centrally, or not quarantined. In addition, due to the fact that the COVID-19 occurred during the Spring Festival in China and the strict prevention and control measures implemented, the epidemic showed significant family clustered (see Footnote 5).
Up to now, a large number of mathematical models have been contributed to study the transmission of COVID-19 and the evaluation of prevention and control measures. These models can be divided into two categories: well-mixed compartment models and heterogeneous mixing network models. Among well-mixed compartment models, the simplest model is to divide individuals into the susceptible, the infectious and the recovered (Roda et al. 2020). Taking into account the quarantine of close contacts, Tang et al. added compartments for quarantined susceptible and latent individuals to the well-mixed model (Tang et al. 2020). Li et al. used a simulation model to investigate the role of two types of hospital beds in controlling the epidemic in Wuhan and concluded that FSHs played a key role in bringing the epidemic to an end (Li et al. 2020a).
Network models consider the contact pattern of human, in which people are regarded as nodes and contacts between people are regarded as links. Xue et al. established a mean-field network model based on node degree to study the spread of the COVID-19 in Wuhan, Toronto and Italy (Xue et al. 2020). Luo et al. used a network pairwise approximation model to study the transmission of COVID-19 in the Chinese mainland (except Hubei) and Hubei provinces, respectively (Luo et al. 2021). This model takes into account both the family cluster and the measure of quarantining close contacts, so as to better reproduce the epidemic prevention and control scene during the COVID-19 in China. None of these models takes into account the effect of medical resources. Although Li et al. studied the effect of FSHs on the COVID-19 epidemic in Wuhan and found that FSHs helped slow and eventually stop the COVID-19 in Wuhan (Li et al. 2020a), they ignored the family cluster and household transmission. In view of the complexity of the COVID-19 prevention and control in Wuhan, none of these models considered the household structure of families of the city due to the complexity.
Considering the significant family cluster transmission of COVID-19, the medical resources in Wuhan and the massive quarantine of close contacts, we build a household model with 123 dimensional to mimic the spread of COVID-19 in Wuhan and to evaluate the impact of medical resources and group quarantine on the spread of COVID-19. The final size of Wuhan is predicted to be 50,662 (95%CI: 46,234, 55,493), and the epidemic will last until April 25 (95%CI: April 23, April 29). It is worth noticing that the final size in this manuscript means that of reported cases. All simulation results show that the key to a successful control of COVID-19 is firstly to track, test and quarantine close contacts and secondly to increase the number of beds to hospitalize and isolate all the confirmed cases. The two complement to each other and are indispensable.
2 Materials and Methods
2.1 Data Collection and Description
We collect all the daily reported data on COVID-19 infections, including the confirmed cases (see Fig. 1a), the recovered cases and death caused by COVID-19 in Wuhan (see Footnote 3). The data are from January 23, 2020, to March 8, 2020. There is a sudden increase in confirmed cases on February 12. This is due to a change in the definition of confirmed cases in Wuhan, which includes clinically confirmed cases.Footnote 7\(^{,}\)Footnote 8\(^{,}\)Footnote 9 We also collect the number of beds in DHs and FSHs (see Footnote 3) (see Fig. 1b). As shown in Fig. 1b), since the first three FSHs were put into use on February 5, the number of beds increased gradually. Until February 27, the number of beds in DHs and FSHs in Wuhan was sufficient,Footnote 10 and there was no need to build new FSHs. As a result, the cumulative number of hospital beds has not changed since February 26. Although FSHs had been shutting downFootnote 11\(^{,}\)Footnote 12 since March 1, this does not affect the prediction of the transmission in Wuhan. According to Statistical Yearbook of Wuhan,Footnote 13 the population of Wuhan is 10,892,900 and the number of households is 3,108,800. But there are no data on the number of different household sizes in Wuhan. We collect the data of the number of different household sizes in Hubei Province, China, from China Statistical Yearbook.Footnote 14 Figure 2 shows the distribution of household size in Hubei Province, China. The household size ranges from one to ten, mostly two and three, and the number of households with seven or more is relatively very small. We will then use the household size distribution of Hubei Province to approximate the distribution of Wuhan.
2.2 The Network Model for COVID-19 in Wuhan with Household Transmission
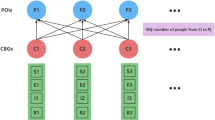
After the lockdown of Wuhan City, family members became the main close contacts of the confirmed cases, and the outbreak is characterized by family cluster transmission. In this scenario, we take households with different sizes as the basic variables and then subdivided these basic variables according to the number of susceptible and infectious within households. There are two ways of transmission: One is within the household, and the other is between the household which is caused by a member of the family going to public places. In view of complex network, Wuhan formed a metapopulation network (as shown in Fig. 3). Nodes in this metapopulation network fall into two categories, one representing a household with size from one to ten and the other representing a public place. All public places are regards as a node here. Members in the unquarantined households can move between their homes and the public place. Individuals in the same household are well mixed and are also well mixed in the public place. In addition, households are divided into quarantined households and unquarantined households based on the presence or absence of a confirmed case in the household. The difference between these two households lies in the following: Individuals in a quarantined household cannot move to the public place and can only contact individuals within the household, while for a unquarantined household, one member each day moves to the public place for a period of time every day and then goes home. Individuals’ movement between different unquarantined households is ignored in view of strict prevention and control measures.
The metapopulation network of Wuhan. Nodes in this metapopulation network fall into two categories, one representing a household and the other representing a public place. Households are further divided into two types: quarantined households and unquarantined households based on whether the presence or absence of a confirmed case
For individuals in Wuhan, this paper divides them into six compartments: susceptible individuals (S) in households, centrally quarantined susceptible (\(S_0\)), infectious individuals (I) in households, centrally quarantined infectious individuals (\(I_0\)), confirmed cases (C) and the removed (recovery or death) (R). Here, an infectious individual is an individual infected with COVID-19 virus and capable of transmitting the virus. I include those infected during the incubation period and those symptomatic infected beyond the incubation period without being confirmed. Although a confirmed individual is also infected with COVID-19 virus, he cannot transmit the virus because of being isolated. S in a unquarantined household may be infected by I within the same household at rate \(\beta _h\) and may randomly move to the public place and be infected by I from other unquarantined households at rate \(\beta _g\). I in a unquarantined household may become confirmed, then hospitalized and isolated after \(1/\mu (t)\) days. Meanwhile, their family members are quarantined at home with probability h, centrally quarantined with probability c, or not quarantined with probability \((1-h-c)\). For quarantined households, S may only be infected by I within the same households at rate \(\beta _h\); I may become confirmed, then hospitalized and isolated after \(1/\mu (t)\) days, while their family members are still quarantined at home. In centrally quarantined points, there is no contact between individuals, so \(S_0\) will not be infected; \(I_0\) may be confirmed, hospitalized and isolated after \(1/\mu (t)\) days. C will be removed after treatment at rate \(\gamma \). In view of strict prevention and control measures in Wuhan City, all confirmed cases and their close contacts are strictly tracked and recorded even after they are released from isolation or quarantine. So we consider that individuals who are released from isolation or quarantine are no longer involved in transmission. Figure 4 provides a detailed flowchart, and the variables and parameters in the flowchart are explained in Table 1.
According to Fig. 4, the following household model is established:
In model (1)–(5), if \(p+q\notin [1,10]\), \(p\notin [0,10]\), or \(q\notin [0,10]\), then \([S_pI_q]=0\); similarly, if \(p+q\notin [1,9]\), \(p\notin [0,9]\), or \(q\notin [0,9]\), then \([S_pI_q]_Q=0\). Since \([S_pI_q]_Q\) is formed when at least one infectious individual in \([S_pI_q]\) is confirmed, \(p+q\in [1,9]\). The dimension of this model is 123 with 65 \([S_pI_q]\) and 55 \([S_pI_q]_Q\).
The model (1)–(5) is explained in detail below. For unquarantined households \([{S_{p}}{I_{q}}]\) [see Eq. (1)], the first and the third terms represent that S are infected by I, including within-household transmission and transmission by I in the public place; the second term represents that I are confirmed and hospitalized; the last term represents that family members are not quarantined when an I of household \([{S_p}{I_{q + 1}}]\) is confirmed. For quarantined households \([{S_{p}}{I_{q}}]_Q\) [see Eq. (2)], the first and the third terms represent that S are infected by I in the same household; the second term represents that I are confirmed and hospitalized; the fourth term represents that family members are quarantined at home when an infectious individual of household \([{S_p}{I_{q + 1}}]\) is confirmed; the last term represents that family members are quarantined at home when an infectious individual of household \([{S_p}{I_{q + 1}}]_Q\) is confirmed. The only term in Eq. (3) represents that S in unquarantined households are centrally quarantined when an infectious individual is confirmed. In Eq. (4), the first term represents that I in unquarantined households are centrally quarantined when an infectious individual is confirmed; the second term represents that I are confirmed. In Eq. (5), the first three terms represent that I are confirmed, and the fourth term represents that C are removed.
The parameter \(1/\mu (t)\) represents the average time from infection to hospitalization (referred to as diagnosis time) of an infectious individual, which depends on the number of beds, newly symptomatic infectious individuals and confirmed cases, as shown in the following equation:
where B(t) is the number of beds at time t; \({C_n}(t)\) represents the number of newly symptomatic infectious individuals and
\(1/{\mu _{\max }}\) is the shortest diagnosis time, and it is approximate to the incubation period; \(1/{\mu _{\min }}\) is the longest diagnosis time.
When \(B(t)\ge C(t) + {C_n}(t)\), that is, the number of beds is sufficient, I will be confirmed and hospitalized as soon as they become symptomatic, so the diagnosis time is approximately equal to the average incubation period (recorded as the shortest diagnosis time). When \(B(t)\le C(t)\), that is, the number of beds is extremely short, newly symptomatic infectious individuals have to wait a long time before being confirmed and hospitalized (recorded as the longest diagnosis time). When \(C(t)< B(t) < C(t) + {C_n}(t)\), only a fraction of newly symptomatic infectious individuals can be confirmed and hospitalized. In this case, the diagnosis time is between the shortest diagnosis time and the longest diagnosis time.
2.3 The Household basic Reproduction Number
The basic reproduction number \({\mathcal {R}}_0\), which is defined as the average number of secondary cases that one case produces during the course of its infectious period in a totally susceptible population, determines the growing rate of an emerging infectious disease. This definition is for individuals, but the main variables of model (1)–(5) are households. So it is necessary to define the household basic reproduction number. Similar to the definition of \({\mathcal {R}}_0\), the household basic reproduction number \({\mathcal {R}}^*\) is defined as the average number of secondary households infected by a household with initially one infectious member during the course of its infectious period in a totally susceptible population. The basic reproduction number is defined for the transmission of infection from individual to individual, while the household basic reproduction number for the transmission of infection from household to household. When all households are of size 1, the household basic reproduction number is the same with the basic reproduction number, that is, \({\mathcal {R}}^*={\mathcal {R}}_0\). \({\mathcal {R}}_0\) is usually calculated by the next-generation matrix method (Van den Driessche and Watmough 2002), so we use the same method to calculate \({\mathcal {R}}^*\).
In the early stages of the spread of COVID-19, medical resources are adequate, so \(\mu (t)={\mu _{\max }}\). Moreover, there are only unquarantined households \([S_pI_q]\,(p + q \in [1,10], p, q \in [0,10])\), so the variables are
the infectious compartments are
and the disease-free equilibrium point is
Adopting the next-generation matrix method (Van den Driessche and Watmough 2002), we have
and
The first row, diagonal and next diagonal of the block matrix  are nonzero matrices; the rest are zero matrices. The diagonal and last diagonal of the block matrix \(V^{55 \times 55}\) are nonzero matrices, and the rest are zero matrices. In detail,
are nonzero matrices; the rest are zero matrices. The diagonal and last diagonal of the block matrix \(V^{55 \times 55}\) are nonzero matrices, and the rest are zero matrices. In detail,

So \({\mathcal {R}}^* = \rho ({F^{55 \times 55}}{({V^{55 \times 55}})^{ - 1}})\), where \(N = \sum _{p = 1}^{10} {[{S_p}{I_0}]}\) and \(\rho (A)\) is the spectral radius of the matrix A. It is difficult to find the explicit expression of \({\mathcal {R}}^*\), but it can be calculated by numerical methods.
3 Parameters Estimation and Numerical Simulations
Based on the collected data and the MCMC (Markov chain Monte Carlo) method (Gamerman and Lopes 2006), this section will estimate the parameters of household model, predict the prevalence trend of COVID-19 in Wuhan City and evaluate the effectiveness of prevention and control measures, including quarantine and medical resources.
3.1 Parameters and Initial Conditions
A total of 152 parameters and initial values of variables are involved in the household model, among which five parameters are derived from the literature, four parameters need to be estimated, and the remaining 143 parameters and initial values need to be pre-calculated.
The five parameters derived from the literature are the shortest diagnosis time (see Footnote 5), the longest diagnosis time (see Footnote 5), the removed rate (Luo et al. 2021), and the population and the total number of households in Wuhan (see Footnote 13) (see Table 2).
The four parameters need to be estimated are the within-household transmission rate \({\beta _h}\), the transmission rate in the public place \({\beta _g}\), household quarantined rate h and centrally quarantined rate c. Based on the cumulative number of confirmed cases and beds collected from January 23 to March 8 in Wuhan, we adopt the MCMC method (Gamerman and Lopes 2006) for 20,000 iterations with a burn-in of 10,000 iterations to fit the model (1)–(5) to estimate these four parameters. A change in the definition of confirmed cases in Wuhan City on February 12 resulted in a sudden increase in 12,000 confirmed cases (as shown in Fig. 1a). Under the new definition of confirmed cases, the cumulative number of confirmed cases reported from January 23 to February 11 underestimated the actual number of confirmed cases. Therefore, in the parameter estimation, different weights are applied to the log-likelihood function around February 12 (the weight after February 12 is greater than before February 12) to obtain more realistic results.
Now, the parameter values and initial values that need to be calculated are given in the following. Firstly, the number of households \(H_k\) with a household size of k in Wuhan is calculated according to the probability distribution \(P(k)(k \in [1,10])\) with a household size of k. Considering that the distribution of household sizes in Wuhan is consistent with that in Hubei Province, according to China Statistical Yearbook, the probability distribution of P(k) with a household size of k in Wuhan is shown in Fig. 2. According to Wuhan Statistical Yearbook, the total number of households in Wuhan is \(H=3{,}108{,}800\), so \(H_k\) can be calculated by the following equation:
Secondly, the initial values of confirmed cases C(0), I in unquarantined household I(0) and the number of individuals quarantined Q (including quarantined infectious individuals and susceptible individuals) are obtained by simple calculations. C(0) equals the difference between the cumulative number of confirmed cases and the cumulative number of removed individuals (the sum of the number of recovered individuals and deaths) at the initial time. The number of newly confirmed cases in one incubation period can be used to approximate I(0). Although the Wuhan Municipal Health Commission has not announced the number of individuals quarantined, the Hubei Provincial Health Commission announced daily data that individuals are quarantined.Footnote 15 According to the ratio of cumulative confirmed cases in Wuhan and Hubei Province, Q can be estimated. Next, we calculate the number of unquarantined households with size \(k>0\) and I being \(q>0\). Considering that the larger the population of households with size k is, the greater the number of I is, and letting \(H_k^I\) be the total number of I in all households with size k at the initial time, we have
According to the principle of randomness of infection and clustering of families, we believe that in an unquarantined household with a size of k with infectious individuals, the number of households with different numbers of infectious individuals \(q (1\le q \le k)\) is equal, which is represented by U(k). For example, when \(k=2\), the number of unquarantined households with infectious individuals \(q=1\) is equal to that with \(q=2\), and both equal to U(2). Then, the total number of infectious individuals in the unquarantined household with size 2 is \(H_2^I = U(2) + 2U(2)\). In a similar way, the total number of infectious individuals in the unquarantined household with size k is \(H_k^E = U(k)\sum _{q = 1}^k q.\) Thus, when \(q > 0\), the initial values of the unquarantined households behave as \([{S_p}{I_q}](0) = U(p+q) = \frac{{H_{p + q}^I}}{{\sum _{i = 1}^{p + q} i }}\). The initial values of quarantined households are calculated in a similar way to that of unquarantined households, which will not be repeated here. All the values of parameters and the initial values are summarized in Tables 2 and 3.
The formulas involved in Tables 2 and 3 are as follows:
3.2 Parameter Estimation
Based on the cumulative number of confirmed cases and beds collected from January 23 to March 8 in Wuhan, we adopt the MCMC method (Gamerman and Lopes 2006) for 20,000 iterations with a burn-in of 10,000 iterations to fit the model (1)–(5) to estimate four parameters (see Table 2). A good fitting between the model solution and real data after February 12 is shown in Fig. 5. On February 12, the definition of confirmed cases in Wuhan changed. Under the new definition of confirmed cases, the reported data before February 12 were lower than the real data, so it is reasonable for the model to overestimate the confirmed cases before February 12. According to Table 2, within-household transmission rate is larger than the transmission rate in the public place. This is due to more frequent within-household contact and individuals staying within household for longer time. The household quarantined rate h is 52.19% (95%CI: 52.13%, 52.25%), and the centrally quarantined rate c is 9.19% (95%CI: 39.15%, 39.24%), which means that on average about 9% of households with confirmed cases are not effectively quarantined.
Based on the estimated parameters, under the current prevention and control measures, the household model predicts that the peak size of Wuhan is 17,356 (95%CI: 16,222, 18,571), that the peak time is on February 15 (95%CI: February 14, February 16), that the final size is 50,662 (95%CI: 46,234, 55,493) and that the time duration is 94 days (95%CI: 92, 98 days) (counting from January 23, 2020). The household basic reproduction number is 11.6540. Compared with the actual situation in Wuhan, the household model does not predict the peak size well. However, the peak time and duration time predicted by the model are only two days away from the actual, and the relative error between the final size and the actual (50,340) is only 0.64%. This indicates that the household model established in this paper is reasonable, and the prediction is more accurate. It is noted that the actual final size of Wuhan did not take into account the imported cases.
Figure 6 illustrates the total number and the distribution of I in the unquarantined household with different sizes. Figure 7 illustrates the number of quarantined infectious individuals (including household quarantined infectious individuals and centrally quarantined infectious individuals) and confirmed cases. It is shown that infectious individuals in the unquarantined households are mainly distributed in household with size from 1 to 6. In detail, the high-risk households are mainly with size from 2 to 4 before the peak time, while the households with size 1 become the most at risk after the peak time. After February 3, the number of infectious individuals in the household with size from 2 to 6 drops sharply. At the same time, the number of quarantined infectious individuals and confirmed cases is still increasing. After February 7, the number of quarantined infectious individuals begins to decrease. It is noticed that Huoshenshan Hospital was put into use from February 4 and that FSHs were put into use from February 5. The increase in the number of beds allowed infectious individuals to be confirmed and hospitalized timely. Meanwhile, their close contacts were also timely quarantined. Prompt confirmation of infectious individuals and prompt quarantine of close contacts led to a rapid reduction in the number of infectious individuals in the unquarantined households. The number of infectious individuals in the unquarantined households with size 1 was slow to reduce after February 3. This is mainly because the number of infectious individuals in such household can only be reduced by confirmation. This also reflects the importance of quarantining close contacts.
3.3 The Effect of Quarantining Close Contacts
For emerging infectious diseases, isolating the infectious and quarantining the susceptible can effectively control the spread of the disease from the source. Figure 8 shows the evolution of the cumulative confirmed cases under different quarantine methods for close contacts. Obviously, centralized quarantine of all close contacts is most conducive to disease prevention and control. If close contacts are not quarantined, the infectious disease will continue for 3 years, and eventually about 87% of Wuhan population will be infected. When quarantining close contacts, the centrally quarantined rate and household quarantined rate can characterize the control of the spread of the COVID-19. The greater the sum of these two rates, the more conducive to the control of the spread of the infectious disease is. If the sum of these two rates is a fixed value, the higher the centrally quarantined rate, the more conducive to the control of the spread of disease is. Therefore, in the prevention and control of infectious diseases, the centralized quarantine of close contacts should be achieved to the greatest extent. Even if centralized quarantine of all close contacts cannot be achieved, strict household quarantine for them is also conducive to the prevention and control of infectious diseases.
The effect of quarantining close contacts on the transmission of COVID-19. Subfigure a shows three extreme cases: purple means no close contacts are quarantined; black means all close contacts are quarantined at home; red means all close contacts are centrally quarantined. Subfigure b compares the case where the centralized quarantine rate and the home quarantine rate are both greater than 0, and the sum of the two is 1 and 0.8, respectively (Color figure online)
Massive centralized quarantine of all close contacts is most conducive to disease prevention and control. However, it will take some time to set up centralized quarantine points. In the event of an emerging infectious disease, it will be difficult to put all close contacts under centralized quarantine immediately. Let \({t_0}\) indicate the start time of the centralized quarantine for all close contacts (\(h=0,c=1\)). Figure 9 compares the cumulative number of confirmed cases under five different \({t_0}\). Before reaching peak time, the sooner all close contacts are quarantined, the better the control of the spread of the disease is. However, when \({t_0}\) exceeds the peak time, achieving complete centralized quarantine has only a slight impact on the final size and duration time.
3.4 The Role of FSHs
Since February 5, 2020, Wuhan has put FSHs with more than 13,000 beds into use. In order to study the necessity of establishing FSHs, this section compares the cumulative confirmed cases and the number of confirmed cases under three cases: whether FSHs are put into use or not, and when the FSHs are established at the same time as city lockdown (as shown in Fig. 10). It is shown that the final size with FSHs is reduced by about 17,000. If the establishment time of FSHs was advanced to January 23, then they could be put into use on January 25 under the assumption that it takes 2 days from establishment to the opening of FSHs. This measure reduces the final size by more than 20,000.
With the opening of the FSHs and the increase in designated hospitals (including the Huoshenshan and Leishenshan hospitals), the number of beds is increasing. On the one hand, the infectious individuals can be timely confirmed and hospitalized, thus reducing the number of deaths due to disease. On the other hand, the prompt confirmation of infectious individuals contributes to the prompt quarantine of close contacts, thus reducing the number of confirmed cases. Based on the daily reported data on infections, it is estimated that the mortality rate due to disease in Wuhan is about 5% by the ratio of the number of cumulative deaths to the cumulative confirmed cases. In order to study the impact of medical resources (number of hospital beds) on the number of deaths, the final size is calculated with a fixed number of hospital beds. The resulting final size is then multiplied by the mortality rate to give a rough estimate of the number of deaths from disease. Figure 11 illustrates the relationship between the number of beds and deaths. The number of deaths is 2512 according to the final size predicted by the household model. As can be seen from Fig. 11, when the number of beds is 8150, the number of deaths is approximate to the estimated value. An increase of just 50 beds could prevent about 360 deaths. The more the beds, the fewer the deaths. But when the number of beds exceeds 11,000, the number of deaths remains about the same, meaning that there are plenty of beds and adding more would have little impact on the infectious disease. This also indicates that the number of deaths would be reduced by about 54.26% if medical resources were adequate at the time of the city lockdown.
4 Discussion
Considering of the prevention and control measures taken after the city lockdown on January 23, 2020, we built a household model with medical sources and quarantining of close contacts. It is found that about 9% of households with confirmed cases are not effectively quarantined. The household model predicted that the final size of Wuhan is 50,662 (95%CI: 46,234, 55,493) and that the outbreak will not end until April 25 (95%CI: April 23, April 29). The predicted peak time and duration time are only 2 days away from the actual ones, and the relative error of the final scale is only 0.64%. The household basic reproduction number was estimated to be 11.6540. It looks overestimated, but it is actually reasonable. The value of household basic reproduction number depends not only on household sizes but also on the value of the basic reproduction number (Ball et al. 1997; Becker and Dietz 1995; Pellis et al. 2011). According to Ref. Li et al. (2020b, 2020c), Nishiura et al. (2020) and Wu et al. (2020b), the basic reproduction number of COVID-19 in Wuhan was estimated to be in the interval [2.23, 6.6037]. According to China Statistical Yearbook and Wuhan Statistical Yearbook, the average household size in Wuhan is 2.9373. For the initially infectious household with an infectious member, which is with the average size 2.9373, the other members soon become infectious since \({\mathcal {R}}_0\in [2.23,6.6037]\). This process takes a very short time. It is equivalent to all members of the household being infectious at the beginning. Then, each member of the infectious household will infect other households. According to the definition of the household basic reproduction number, a household with the average size 2.9373 may infect 6.5502–19.3970 households. Hence, the estimated household reproduction number was reasonable.
By studying the effects of different times and degrees of quarantine of close contacts on the cumulative confirmed cases, we found that not quarantining close contacts will eventually result in about 87% of infections. Moreover, it is found that putting FSHs into use reduced the final size by about 17,000. If the establishment time of FSHs started on January 23, 2020, immediately after the lockdown, the final size may be reduced by 20,000. If the medical resources are adequate at the time of Wuhan lockdown, the number of deaths may be reduced by nearly 54.26%. It is also shown that the high-risk households are mainly with size from 2 to 4 before the peak time, while the households with size 1 become the most at risk after the peak time. Based on the above analysis results, the keys to the success of COVID-19 prevention and control in Wuhan are to adopt tracking and quarantine measures for close contacts and to open the FSHs and increase DHs for isolating and curing confirmed cases.
Compared with other mathematical models for COVID-19, the dimension of this household model (123) is very high, but the advantages of the model are significant. On the one hand, this model reflects the characteristics of family cluster of COVID-19 which is an extension of the modeling in Li et al. (2020a). On the other hand, this model can depict the evolution of infectious individuals in household with different sizes and indicate high-risk household type. Moreover, fine division of compartment allows this model to well reproduce the process of COVID-19 transmission and control in Wuhan. The conclusions obtained are more credible. Our findings of the successful experience in Wuhan can help the prevention and control of similar emerging infectious diseases and also provide a good reference for COVID-19 prevention and control in other places of the world.
This paper also has some limitations. Taking into account the strict implementation of Wuhan’s epidemic prevention and control measures, this paper believes that people who have been quarantined or isolated (whether susceptible people are released from quarantine or confirmed cases are removed after hospitalization) will no longer participate in transmission. This is a simplification of the household model. When individuals in Wuhan are divided into susceptible S, infectious I, confirmed C, recovered R and dead D, the flowchart is shown in Fig. 12. The household is divided into quarantined household and unquarantined household based on the presence or absence of quarantined individuals. \([S_s^0I_i^0C_cR_rD_d]\) is defined as the number of unquarantined households in which the number of S, I, C, R, D is s, i, c, r, d, respectively. Here, \((s,i,c,r,d)\in \{(s,i,c,r,d)\in {\mathbb {N}}^5\mid s+i+c+r+d\in [1,10]\}\). \([S_0^sI_0^iC_cR_rD_d]\) denotes the number of quarantined households in which the number of S, I, C, R, D is s, i, c, r, d, respectively. Here, \((s,i,c,r,d)\in \{(s,i,c,r,d)\in {\mathbb {N}}^5\mid s+i+c+r+d\in [2,10],s+i\geqslant 1,c+r+d\geqslant 1\}\). For this household model with detailed division, its dimension is more than 5600. It can also be used to study the transmission of COVID-19. However, such a high dimension makes it more difficult to select the initial values of the variables and makes the program run slower. Therefore, it is necessary to simplify the model reasonably. The model (1)–(5) is one of the reasonable simplifications of this model. According to China Statistical Yearbook, household sizes in China are divided into 10 categories: 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 and above. The number of households with size larger than 10 is counted together with those with size 10, and it is small compared to that of other sizes. In addition, considering that gatherings of more than 10 people were prohibited during COVID-19, we set the size of households with 10 and above to be 10. We will collect more detailed data and expand household size in the future work.
The flowchart of household model with more detailed division. The black solid lines represent infection; the black dashed lines are caused by the transformation of C; the yellow lines mean that I is confirmed and that his family members are quarantined; the gray line indicates the release of quarantine (Color figure online)
Although the household model established in this paper is for the megacity of Wuhan, it could be extended to study of COVID-19 in other countries and regions. When applied to other provinces and cities in China, medical resources are adequate, so \(\mu (t)\) should be constant; there is no household quarantine, so \(h=0,c=1\) and \([S_pI_q]_Q=0\). When analyzing other countries, the status of family members and the household sizes may vary. The detailed division will result in higher model dimensions which is more complicated; we will keep it as future work.
Data Availability
All relevant data during this study are included in this published article.
Notes
National Health Commission of the People’s Republic of China. http://www.nhc.gov.cn/.
Wuhan Novel Coronavirus Pneumoinfection Prevention and Control Headquarters Notification (No.1). http://www.gov.cn/xinwen/2020-01/23/content_5471751.htm.
Wuhan Municipal Health Commission. http://wjw.wuhan.gov.cn.
Johns Hopkins University Coronavirus resource center. https://coronavirus.jhu.edu/map.html.
Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19). https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf.
Central People’s Government of the People’s Republic of China. http://www.gov.cn/xinwen/2020-02/06/content_5475062.htm.
Data of COVID-19 in Wuhan on February 12, 2020. http://wjw.wuhan.gov.cn/ztzl_28/fk/yqtb/202004/t20200430_1197352.shtml.
Diagnosis and treatment plan for covid-19 (trial version 4). http://www.nhc.gov.cn/yzygj/s7653p/202001/4294563ed35b43209b31739bd0785e67.shtml.
Diagnosis and treatment plan for covid-19 (trial version 5). http://www.nhc.gov.cn/yzygj/s7653p/202002/d4b895337e19445f8d728fcaf1e3e13a.shtml.
The number of beds is adequate. http://news.cri.cn/20200301/5aa1713e-712e-4ed5-d5af-b77b3cf3595d.html.
The first Fangcang shelter hospital is closed. https://baijiahao.baidu.com/s?id=1660105374181532222&wfr=spider&for=pc.
The last Fangcang shelter hospital is closed. https://m.chinanews.com/wap/detail/zw/sh/2020/03-11/9121442.shtml.
Wuhan Statistical Yearbook. http://tjj.hubei.gov.cn/tjsj/sjkscx/tjnj/gsztj/whs/.
China Statistical Yearbook. http://www.stats.gov.cn/tjsj/ndsj/2019/indexch.htm.
Health Commission of Hubei Province. http://wjw.hubei.gov.cn/.
References
Ball F, Mollison D, Scalia-Tom Ba G (1997) Epidemics with two levels of mixing. Ann Appl Probab 7(1):46–89. https://doi.org/10.2307/2245132
Becker NG, Dietz K (1995) The effect of household distribution on transmission and control of highly infectious diseases. Math Biosci 127:207–219. https://doi.org/10.1016/0025-5564(94)00055-5
Chan J, Yuan S, Kok K et al (2020) A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet 395(10223):514–523. https://doi.org/10.1016/S0140-6736(20)30154-9
Chen S, Zhang Z, Yang J et al (2020) Fangcang shelter hospitals: a novel concept for responding to public health emergencies. Lancet 395(10232):1305–1314. https://doi.org/10.1016/S0140-6736(20)30744-3
Chinazzi M, Davis JT, Ajelli M et al (2020) The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 368(6489):395–400. https://doi.org/10.1126/science.aba9757
Gamerman D, Lopes HF (2006) Markov chain Monte Carlo: stochastic simulation for Bayesian inference. Chapman and Hall/CRC
Huang C, Wang Y, Li X et al (2020) Clinical features of patients infected with 2019 novel coronavirus in Wuhan. China. Lancet 395:497–506. https://doi.org/10.1016/S0140-6736(20)30183-5
Li J, Yuan P, Heffernan J et al (2020a) Fangcang shelter hospitals during the COVID-19 epidemic, Wuhan, China. Bull World Health Organ 98(12):830-841D. https://doi.org/10.2471/BLT.20.258152
Li RY, Pei S, Chen B et al (2020b) Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 368:489–493. https://doi.org/10.1126/science.abb3221
Li Y, Wang LW, Peng ZH et al (2020c) Basic reproduction number and predicted trends of coronavirus disease 2019 epidemic in the mainland of China. Infect Dis Poverty 9:94. https://doi.org/10.1186/s40249-020-00704-4
Luo X, Feng S, Yang J et al (2021) Nonpharmaceutical interventions contribute to the control of COVID-19 in China based on a pairwise model. Infect Dis Model 6:643–663. https://doi.org/10.1016/j.idm.2021.04.001
Pellis L, Ferguson NM, Fraser C (2011) Epidemic growth rate and household reproduction number in communities of households, schools and workplaces. J Math Biol 63:691–734. https://doi.org/10.1007/s00285-010-0386-0
Roda WC, Varughese MB, Han D et al (2020) Why is it difficult to accurately predict the COVID-19 epidemic? Infect Dis Model 5:271–281. https://doi.org/10.1016/j.idm.2020.03.001
Tang B, Wang X, Li Q et al (2020) Estimation of the transmission risk of 2019-nCov and its implication for public health inverventions. J Clin Med 9:462. https://doi.org/10.3390/jcm9020462
Nishiura H, Linton NM, Akhmetzhanov AR (2020) Initial cluster of novel coronavirus (2019-nCoV) infections in Wuhan, China is consistent with substantial human-to-human transmission. J Clin Med 9(2):488. https://doi.org/10.3390/jcm9020488
Van den Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48. https://doi.org/10.1016/S0025-5564(02)00108-6
Wu P, Hao X, Lau EHY et al (2020a) Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China, as at 22 January 2020. Euro Surveill 25(3):2000044. https://doi.org/10.2807/1560-7917.ES.2020.25.3.2000044
Wu JT, Kathy L, Leung GM (2020b) Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet 395:689–697. https://doi.org/10.1016/S0140-6736(20)30260-9
Wells CR, Sah P, Moghadas SM et al (2020) Impact of international travel and border control measures on the global spread of the novel 2019 coronavirus outbreak. Proc Natl Acad Sci USA 117(13):202002616. https://doi.org/10.1073/pnas.2002616117
Xue L, Jing S, Miller JC et al (2020) A data-driven network model for the emerging COVID-19 epidemics in Wuhan, Toronto and Italy. Math Biosci 326. https://doi.org/10.1016/j.mbs.2020.108391
Funding
This work is supported by the National Natural Science Foundation of China Grants 61873154, Health Commission of Shanxi Province Grants 2020XM18, Shanxi Provincial Department of Science and Technology COVID-19 Emergency Special Fund grants 202003D31011/GZ and Fundamental Research Program of Shanxi Province Grants 20210302124608 and 20210302124381.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Feng, S., Zhang, J., Li, J. et al. The Impact of Quarantine and Medical Resources on the Control of COVID-19 in Wuhan based on a Household Model. Bull Math Biol 84, 47 (2022). https://doi.org/10.1007/s11538-021-00989-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11538-021-00989-y