JEE Main 2019 Maths question paper pdf is provided which consists of step by step solutions prepared by our subject experts. These solutions for the questions have been carefully structured and written in a simple language for better understanding. These will help students to grasp the concepts and solve problems easily. Practising these solutions will further help them to analyze their preparation level, identify their weak areas and concentrate on improving them. Students can easily download the question paper and solutions in PDF format below.
JEE Main 2019 Question Papers
January 2019 Maths Paper
Question 1. There are 5 girls and 7 boys. A team of 3 boys and 2 girls is to be formed such that no two specific boys are in the same team. Number of way to do so
a) 400
b) 250
c) 200
d) 300
Total number of teams = 7C3× 5C2
= 35×10 = 350
Let A, B be the specific boys.
Number of teams with these two boys in the same team = 5C1 × 5C2
= 5×10 = 50
Required number of ways = 350-50 = 300
Answer:(d)
Question 2. The equation x2+2x+2 = 0 has roots α and β. Then value of α15 + β15is;
a) 512
b) 256
c) -512
d) -256
Solution:
(x+1)2 = -1 ⇒ x+1 = ±i
x = -1+I, -1-i
α = -1+I, β = -1-i
α = √2ei(3π/4), β = √2ei(-3π/4)
α15+ β15 = (√2)15(ei(45π/4) + ei(-45π/4))
= 215/2(2 cos(45π/4))
= 215/2 (2×-1/√2)
= -28
= -256
Answer: (d)
Question 3. \(\begin{array}{l}\int_{0}^{\pi }\left | \cos x \right |^{3}dx\end{array} \)
is equal to;
a) 4/3
b) 2/3
c) 0
d) 8/3
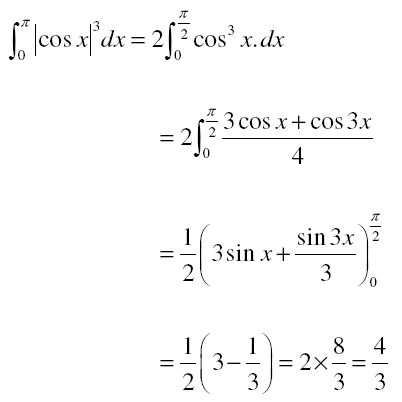
Answer: (a)
Question 4. If x2 ≠ nπ+1, n ∈N, then \(\begin{array}{l}\int x \sqrt{\frac{2 \sin \left(x^{2}-1\right)-\sin 2\left(x^{2}-1\right)}{2 \sin \left(x^{2}-1\right)+\sin 2\left(x^{2}-1\right)}} d x\end{array} \)
is equal to
a) \(\begin{array}{l}ln \cos \left ( \frac{x^{2}-1}{2} \right )+c\end{array} \)
b) \(\begin{array}{l}\frac{1}{2}ln \cos \left ( \frac{x^{2}-1}{2} \right )+c\end{array} \)
c) \(\begin{array}{l}ln \sec \left ( \frac{x^{2}-1}{2} \right )+c\end{array} \)
d) \(\begin{array}{l}\frac{1}{2}ln \sec \left ( \frac{x^{2}-1}{2} \right )+c\end{array} \)
Let x2-1 = t
2x dx = dt
x dx = dt/2
\(\begin{array}{l}\int \sqrt{\frac{2 \sin t-\sin 2 t}{2 \sin t+\sin 2 t}} \cdot \frac{d t}{2}=\frac{1}{2} \int \sqrt{\frac{2 \sin t(1-\cos t)}{2 \sin t(1+\cos t)}} \cdot d t\end{array} \)
=
\(\begin{array}{l}\frac{1}{2}\int \tan \frac{t}{2}.dt\end{array} \)
=
\(\begin{array}{l}log\left | \sec \frac{t}{2} \right |+c\end{array} \)
=
\(\begin{array}{l}log\left | \sec \left ( \frac{x^{2}-1}{2} \right )\right |+c\end{array} \)
Answer: (c)
Question 5. If \(\begin{array}{l}\vec{a}=i -j\end{array} \)
, \(\begin{array}{l}\vec{b}=i +j+k\end{array} \)
are two vectors, and c is another vector such that \(\begin{array}{l}\vec{a}\times \vec{c}+\vec{b}=\vec{0}\end{array} \)
and \(\begin{array}{l}\vec{a}. \vec{c}=4\end{array} \)
then \(\begin{array}{l}\left | \vec{c}\right |^{2} =\end{array} \)
a) 9
b) 8
c) 19/2
d) 17/2
\(\begin{array}{l}\vec{a}\times \vec{c}+\vec{b}=\vec{0}\end{array} \)
\(\begin{array}{l}\vec{a}\times \vec{c}=-\vec{b}\end{array} \)
\(\begin{array}{l}\vec{a\times }\left ( \vec{a}\times \vec{c}\right )=\vec{b}\times \vec{a}\end{array} \)
\(\begin{array}{l}\left ( \vec{a}. \vec{c}\right )\vec{a} – \left ( \vec{a}. \vec{a}\right )\vec{c}=\vec{b}\times \vec{a}\end{array} \)
..(i)
\(\begin{array}{l}\left ( \vec{a}. \vec{c}\right )=4 \; and \left ( \vec{a}. \vec{a}\right )=2\end{array} \)
..(ii)
\(\begin{array}{l}\vec{b}\times \vec{a}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 1& 1 & 1\\ 1&-1 & 0 \end{vmatrix} = \hat{i}+\hat{j}-2\hat{k}\end{array} \)
..(iii)
From (i), (ii) and (iii)
\(\begin{array}{l}4\vec{a}-2\vec{c}= \hat{i}+\hat{j}-2\hat{k}\end{array} \)
\(\begin{array}{l}-2\vec{c}= \hat{i}+\hat{j}-2\hat{k}-4( \hat{i}- \hat{j})\end{array} \)
\(\begin{array}{l}-2\vec{c}= -3\hat{i}+5\hat{j}-2\hat{k}\end{array} \)
\(\begin{array}{l}4\left | \vec{c}\right |^{2} =38\end{array} \)
\(\begin{array}{l}\left | \vec{c}\right |^{2} =\frac{19}{2}\end{array} \)
Answer: (c)
Question 6.If
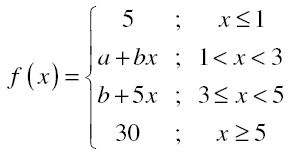
then:
a) f (x) is discontinuous ∀ a ∈ R, b ∈ R
b) f (x) is continuous if a = 0 & b = 5
c) f (x) is continuous if a = 5 & b = 0
d) f (x) is continuous if a = -5 & b = 10
f(1–) = f(1+)
a+b = 5 ..(i)
f(3+) = f(3–)
b+15 = a+3b ..(ii)
f(5+) = f(5–)
b + 25 = 30 … (iii)
From (iii), b = 5
From (i), a = 0 & from (ii), a = 5
f ( x) is discontinuous ∀a ∈R, b∈ R
Answer: (a)
Question 7. Average height and variance of 5 students in a class is 150 and 18 respectively. A new student whose height is 156 cm is added to the group. Find new variance.
a) 20
b) 22
c) 16
d) 14
Let 5 students are x1 , x2 , x3 , x4 , x5
Given
\(\begin{array}{l}\bar{x}= \frac{\sum x_{i}}{5}= 150\end{array} \)
Ʃxi = 750 ..(i)
\(\begin{array}{l}\frac{\sum x_{i}^{2}}{5}-(\bar{x})^{2}= 18\end{array} \)
\(\begin{array}{l}\frac{\sum x_{i}^{2}}{5}-(150)^{2}= 18\end{array} \)
\(\begin{array}{l}\sum x_{i}^{2}= (22500+18)\times 5\end{array} \)
\(\begin{array}{l}\sum x_{i}^{2}= 112590\end{array} \)
..(ii)
Height of new student = 156 (Let x6)
Now x1+ x2+ x3+x4 +x5+x6 = 750+156
\(\begin{array}{l}\bar{x}_{new} = \left ( \frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}}{6} \right )=\frac{906}{6}=151\end{array} \)
..(iii)
Variance (new) =
\(\begin{array}{l}\frac{\sum x_{i}^{2}}{6}-(\bar{X})^{2}\end{array} \)
= [(x12 + x22+ x32+ x42+ x52+ x62)/6]-(151)2
From equation (2) and (3)
Var(new) = [112590+(156)2/6] – (151)2
= 22821 – 22801
= 20
Answer: (a)
Question 8. a,b,c are in G.P. a+b+c = bx , then x cannot be;
a) 2
b) -2
c) 3
d) 4
Let the terms of G.P be a/r, a, ar
(a/r) + a+ar = ax
x = r+(1/r)+1
But r+(1/r) ≥ 2
Or r+(1/r) ≤ -2 ( using A.M,G.M inequality )
x-1 ) ≥ 2 or x-1 ≤ -2
x ≥ 3 or x ≤ -1
So x cannot be 2.
Answer: (a)
Question 9.{2403/15} = k/15 then find k. (where {.} denotes fractional part function).
a) 2
b) 8
c) 1
d) 4
Solution:
24 ≡ 1 (mod 15)
2400 ≡ 1 (mod 15)
2403 ≡ 8(mod 15)
{2403/15} = 8/15
k = 15
Answer: (b)
Question 10. \(\begin{array}{l}\lim_{y\to 0}\frac{\sqrt{1+\sqrt{1+y^{4}}}-\sqrt{2}}{y^{4}}\end{array} \)
=
a) 1/4√2
b) 1/2√2
c) 1/2√2(1+√2)
d) does not exist
Rationalising numerator,
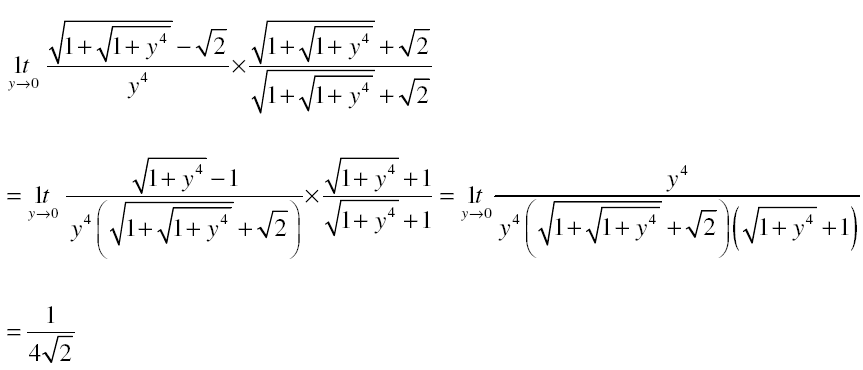
Answer: (a)
Question 11.There is a parabola having axis as x-axis, vertex is at a distance of 2 unit from origin & focus is at (4, 0). Which of the following point does not lie on the parabola.
a) (6, 8)
b) (5, 2√6)
c) (8, 4√3)
d) (4,-4)
The equation of parabola is y2 = 8(x-2)
(6,8) does not lie on this curve.
Answer: (a)
Question 12. Find sum of all possible values of θ in the interval (-π/2, π) for which \(\begin{array}{l}\frac{3+2i\sin \theta }{1-2i\sin \theta}\end{array} \)
is purely imaginary;
a) π/3
b) π
c) 2π/3
d) π/2
\(\begin{array}{l}z=\frac{3+2i\sin \theta }{1-2i\sin \theta}\times \frac{1+2i\sin \theta}{1+2i\sin \theta}\end{array} \)
=
\(\begin{array}{l}\frac{3-4\sin ^{2}\theta+i(8\sin \theta ) }{1+4\sin^{2} \theta}\end{array} \)
For z to be purely imaginary, Re(z) = 0
i.e
\(\begin{array}{l}\frac{3-4\sin ^{2}\theta }{1+4\sin^{2} \theta}=0\end{array} \)
sin2 θ = 3/4
As θ∈ (-π/2,π ) = ±π/3, 2π/3
Sum of all values of θ = 2π/3
Answer: (c)
Question 13.Let A = \(\begin{array}{l}\begin{bmatrix} \cos \theta &-\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\end{array} \)
find the value of A-50 at θ = π/12.
a) \(\begin{array}{l}\begin{bmatrix} -\frac{\sqrt{3}}{2} & -\frac{1}{2}\\ -\frac{1}{2}& \frac{\sqrt{3}}{2} \end{bmatrix}\end{array} \)
b) \(\begin{array}{l}\begin{bmatrix} \frac{\sqrt{3}}{2} & \frac{1}{2}\\ -\frac{1}{2}& \frac{\sqrt{3}}{2} \end{bmatrix}\end{array} \)
c) \(\begin{array}{l}\begin{bmatrix} -\frac{\sqrt{3}}{2} & \frac{1}{2}\\ \frac{1}{2}& \frac{\sqrt{3}}{2} \end{bmatrix}\end{array} \)
d) \(\begin{array}{l}\begin{bmatrix} \frac{{1}}{2} & \frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& -\frac{{1}}{2} \end{bmatrix}\end{array} \)
A =
\(\begin{array}{l}\begin{bmatrix} \cos \theta &-\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\end{array} \)
A is a rotation matrix.
An =
\(\begin{array}{l}\begin{bmatrix} \cos n\theta &-\sin n\theta \\ \sin n\theta & \cos n\theta \end{bmatrix}\end{array} \)
A-50 =
\(\begin{array}{l}\begin{bmatrix} \cos 50\: \theta &\sin 50\: \theta \\ -\sin 50\: \theta & \cos 50\: \theta \end{bmatrix}\end{array} \)
A-50 at θ= π/2 is
\(\begin{array}{l}\begin{bmatrix} \cos \frac{25\pi }{6}\: &\sin \frac{25\pi }{6}\: \\ -\sin \frac{25\pi }{6}\: & \cos \frac{25\pi }{6}\: \end{bmatrix}\end{array} \)
=
\(\begin{array}{l}\begin{bmatrix} \frac{\sqrt{3}}{2} & \frac{1}{2}\\ -\frac{1}{2}& \frac{\sqrt{3}}{2} \end{bmatrix}\end{array} \)
Answer: (b)
Question 14. If (A⊕B)∧(∼ A⊝ B)
= \(\begin{array}{l}A\wedge B\end{array} \)
what should be proper symbol in place of \(\begin{array}{l}\oplus\end{array} \)
and ⊝ to hold the equation
a) \(\begin{array}{l}\wedge and\vee\end{array} \)
b) \(\begin{array}{l}\wedge and\wedge\end{array} \)
c) \(\begin{array}{l}\vee and\vee\end{array} \)
d) \(\begin{array}{l}\vee and\wedge\end{array} \)
By inspection ⊕ represents ∧ and ⊝ represents ∨
|
A
|
B
|
A∧B
|
~A
|
~A∨B
|
(A∧B)∧ (~A∨B)
|
|
T
|
T
|
T
|
F
|
T
|
T
|
|
T
|
F
|
F
|
F
|
F
|
F
|
|
F
|
T
|
F
|
T
|
T
|
F
|
|
F
|
F
|
F
|
T
|
T
|
F
|
(A∧B)∧(~A∨B)≡ A∧B
Answer: (a)
Question 15. If y (x) is solution of x(dy/dx) +2y = x2, y(1) = 1, then value of y(1/2)
a) -49/16
b) 49/16
c) 45/8
d) -45/8
x(dy/dx) + 2y = x2
(dy/dx) + 2y/x = x
This is linear differential equation.
I.F =e ∫(2/x)dx = e2 log x = x2
solution is x2y = ∫x3 dx
x2y = (x4/4) + c
y(1) = 1 c = ¾
at x = 1/2 (¼)y = (1/64) +(3/4)
y = 49/16.
Answer: (b)
Question 16. From a well shuffled deck of cards, 2 cards are drawn with replacement. If x represent numbers of times ace coming, then value of P(x = 1) + P(x = 2) is;
a) 25/169
b) 24/169
c) 49/169
d) 23/169
P(x = 1) = 2C1×(4/52)×(48/52) = 24/169
P(x = 2) = 2C2×(4/52)2= 1/169
P(x = 1) + P(x = 2) = 25/169
Answer: (a)
Question 17. If eccentricity of the hyperbola \(\begin{array}{l}\frac{x^{2}}{\cos ^{2}\theta }-\frac{y^{2}}{\sin ^{2}\theta } =1\end{array} \)
is more than 2 when ∈(0, π/2) then values of length of latus rectum lies in the interval
a) (3, ∞)
b) (1, 3/ 2)
c) (2, 3)
d) (-3, -2)
For hyperbola, e2 = 1+(b2/a2)
= 1+tan2 θ
= sec2θ
e>2 ⇒ sec θ > 2
∈(π/3, π/2)
Length of latus rectum =2b2/a = 2 tan θ sin θ
= 2(>√3)(> √3/2)
> 3
Answer (a)
Question 18. If slant height of a right circular cone is 3 cm then the maximum volume of cone is
a) 2√3 πcm3
b) 4√3 πcm3
c) (2+√3) πcm3
d) (2-√3) πcm3
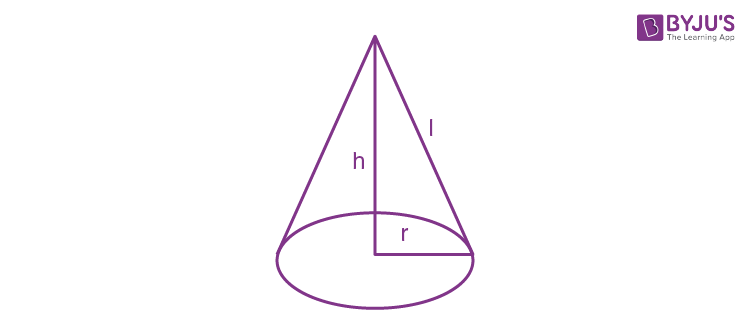
l = 3
r2 + h2 = 9
r2 = 9 -h2
V = (1/3)πr2h
= (1/3)πh(9 -h2)
V = 3πh – 1/3πh3
For maximum volume, dv/dh = 0
3π – πh2 = 0
h2 = 3
h = √3
r2 = 6
Volume = (1/3)π (6)(√3) = 2√3 πcm3
Answer (a)
Question 19. If cos-1(2/3x) + cos-1(3/4x) = π/2, x>3/4 then x =
a) √145/11
b) √145/12
c) √146/10
d) √146/11
cos-1 (2/3x) = π/2 – cos-1(3/4x)
cos-1 (2/3x) = cos-1 (√(16x2-9)/4x
2/3x = (√(16x2-9)/4x
(√(16x2-9) = 8/3
16x2-9 = 64/9
x2 = 145/(9×16)
x = √145/12
Answer: (b)
Question 20. If px+qy+r = 0 represent a family of straight lines such that 3p+2q+4r = 0 then;
a) All lines are parallel
b) All lines are inconsistent
c) All lines are concurrent at (3/4, 1/2)
d) All lines are concurrent at (3,2)
Px+qy+r = 0 … (i)
3p+2q+4r = 0
(3p/4) +(q/2) +r = 0 ..(ii)
(i) and (ii) are identical.
\(\begin{array}{l}\frac{x}{\frac{3}{4}} = \frac{y}{\frac{1}{2}}=1\end{array} \)
x = 3/4 and y = 1/2.
Answer: (d)
Question 21. Consider the system of equations x+y+z = 1, 2x+3y+2z =1, 2x+3y+(a2 -1)z = a+1 then
a) system has a unique solution for ǀaǀ = √3
b) system is inconsistence for ǀaǀ = √3
c) system is inconsistence for a = 4
d) system is inconsistence for a = 3
x + y + z = 1 … (i)
2x + 3y + 2z = 1 … (ii)
2x + 3y + (a2 −1)z = a +1 …(iii)
By observation, when a2-1 = 2
LHS of (ii) & (iii) are same but RHS different
Hence a2 = 3 ⇒ ǀaǀ = √3
For ǀaǀ = √3, the system is inconsistent.
Answer: (b)
Question 22.The value of 3(cos θ – sin θ)4 + 6(sin θ + cos θ)2+4 sin6θ is, where θ∈ (π/4, π/2)
a) 13-4 cos4θ
b) 13-4 cos6θ
c) 13-4 cos6θ+2 sin4θ cos2θ
d) 13-4 cos4θ+2 sin4θ cos2θ
3(cos2 θ+ sin2 θ -sin 2θ)2 +6(sin2 θ+ cos2 θ+ sin 2θ) +4sin6θ
= 3(1+sin2 2θ – 2sin 2θ)+6+6sin 2θ+4sin6θ
= 9+3sin2 2θ +4 sin6θ
= 9+3(4 sin2θ cos2θ)+4(1-cos2θ)3
= 9+12 cos2θ sin2θ+4(1-cos6θ-3 cos2θ sin2θ)
= 9+12 sin2θ cos2θ +4-4 cos6θ-12 sin2θ cos2θ)
= 13 – 4 cos6θ
Answer: (b)
Question 23. 3 circles of radii a, b, c (a < b < c) touch each other externally and have x – axis as a common tangent then;
a) a, b, c are in A.P.
b) 1/√b = (1/√a) + (1/√c)
c) √a, √b, √c are in A.P.
d) (1/√c) + (1/√b) = (1/√a)
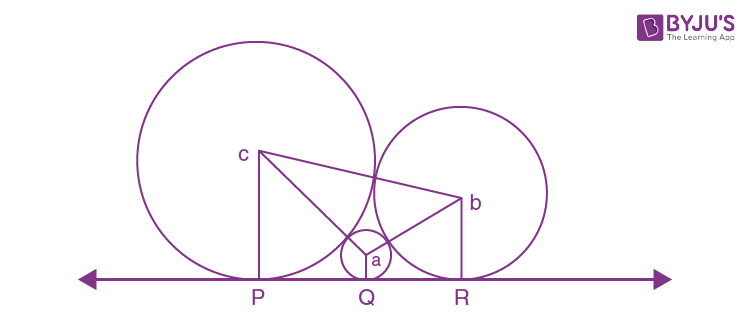
PQ +QR = PR
\(\begin{array}{l}\sqrt{(c+a)^{2}-(c-a)^{2}}+\sqrt{(b+a)^{2}-(b-a)^{2}}=\sqrt{(b+c)^{2}-(c-b)^{2}}\end{array} \)
√(4ac) + √(4ab) = √(4bc)
Dividing with √(4abc)
(1/√b) + (1/√c) = (1/√a)
Answer: (a)
Question 24.If f(x) = 1/x, f2(x) = 1-x, f3(x) = 1/(1-x) then find J(x) such that f2oJof1(x) = f3(x)
a) f1(x)
b) (1/x) f3(x)
c) f3(x)
d) f2(x)
f2(J(f1(x))) = f3(x)
f2(J(1/x)) = 1/(1-x)
1-J(1/x) = 1/(1-x)
J(1/x) = 1-(1/(1-x)) = x/(x-1)
J(x) = 1/(1-x) = f3(x)
Answer: (c)
Question 25.Find the equation of line through (−4,1,3) and parallel to the plane x + y + z = 3 while the line intersects another line whose equation is x + y – z = 0 = x + 2y -3z + 5;
a) \(\begin{array}{l}\frac{x+4}{-3}= \frac{y-1}{-2}=\frac{z-3}{1}\end{array} \)
b) \(\begin{array}{l}\frac{x+4}{1}= \frac{y-1}{2}=\frac{z-3}{1}\end{array} \)
c) \(\begin{array}{l}\frac{x+4}{-3}= \frac{y-1}{2}=\frac{z-3}{1}\end{array} \)
d) \(\begin{array}{l}\frac{x+4}{-1}= \frac{y-1}{2}=\frac{z-3}{-3}\end{array} \)
Family of planes containing the line of intersection of planes is π1 +λπ2 = 0
i.e. (x +y -z) +λ(x +2y -3z +5) = 0
This is passing through (-4,1,3)
λ= -1
Hence the equation of plane is y -2z + 5 = 0
Required line is lie in this plane and is parallel to x + y + z = 5
direction of required line =
\(\begin{array}{l}\begin{vmatrix} \hat{i} & \hat{j} &\hat{k} \\ 1& 1 & 1\\ 0 & 1 & -2 \end{vmatrix}\end{array} \)
=
\(\begin{array}{l}-3\hat{i}+2\hat{j}+\hat{k}\end{array} \)
Required line is
\(\begin{array}{l}\frac{x+4}{-3}= \frac{y-1}{2}=\frac{z-3}{1}\end{array} \)
Answer (c)
Question 26.Consider the curves y = x2 +2 and y = 10-x2. Let θ be the angle between both the curves at point of intersection, then find ǀtan θǀ
a) 8/15
b) 5/17
c) 3/17
d) 8/17
x2 +2 = 10-x2
x = ±2 and y = 4
Point of intersection of curves = (±2, 4)
y = x2+2; y = 10-x2
(dy/dx) = 2x; (dy/dx) = -2x
(dy/dx) at (±2, 4) = ±4 = m1; (dy/dx) at (±2, 4) = ±4 = m2
ǀtan θǀ = ǀ8/(1-16)ǀ
= 8/15
Answer (a)
Question 27.A plane parallel to y-axis passing through line of intersection of planes x+y+z =1 and 2x+3y-z-4 = 0 which of the point lie on the plane.
a) (3,2,1)
b) (−3,0,1)
c) (−3,1,1)
d) (3,1,−1)
Required plane is π1+ λπ2 = 0
(x+y+z-1)+λ(2x+3y-z-4) = 0
(1+2λ)x+(1+3λ)y+(1-λ)z-(1+4λ) = 0
This is parallel to y axis ⇒ λ = -1/3
Required plane is x+4z+1 = 0
By inspection, (3,1,-1) lie in this plane.
Answer (d)
Question 28.Find common tangent of the two curves y2 = 4x and x2+y2-6x = 0.
a) y = (x/3)+3
b) y = (x/√3) -√3
c) y = (x/3)-3
d) y = (x/√3) +√3
Equation of tangent to the parabola y2 = 4x is y = mx+(1/m)
m2x-my+1 = 0
This is also tangent to x2+y2-6x = 0.
i.e.,
\(\begin{array}{l}\left | \frac{3m^{2}+1}{\sqrt{m^{4}+m^{2}}} \right |=3\end{array} \)
9m4+1+6m2 = 9m4+9m2
3m2 = 1
m = ±1/√3
The common tangent is y = ±((x/√3)+√3)
Answer (1)
Question 29.
The area bounded by the curve y = x2 -1, tangent to it at (2, 3) and y-axis is;
a) 2/3
b) 4/3
c) 8/3
d) 1
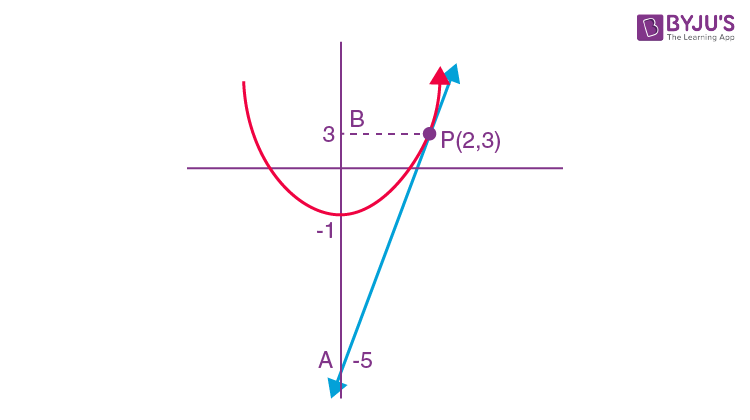
Equation of tangent at (2, 3) is
(y+3)/2 = 2x-1
y+3 = 4x-2
4x-y = 5
Required area = Ar(PAB) –
\(\begin{array}{l}\int_{-1}^{3}x_{parabola}dy\end{array} \)
=
\(\begin{array}{l}\frac{1}{2}\times 2\times 8-\int_{-1}^{3}\sqrt{y+1}dy\end{array} \)
=
\(\begin{array}{l}8-\frac{2}{3}\left ( (y+1)^{\frac{3}{2}} \right )^{3}_{-1}\end{array} \)
= 8-(16/3)
= 8/3
Answer (c)
Download PDF Here
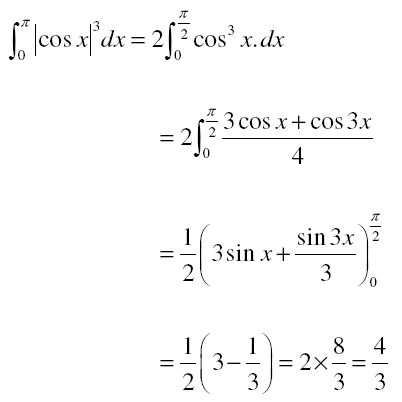
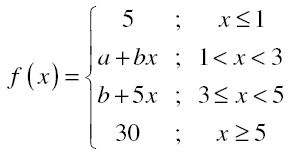
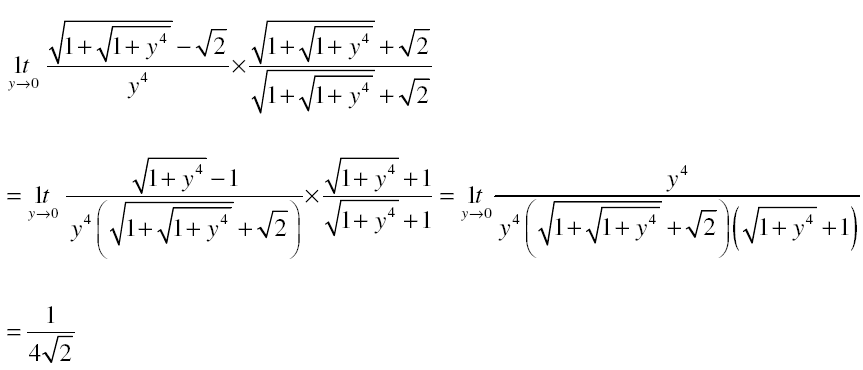




























Comments