Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017;112(520):1430-1442.
doi: 10.1080/01621459.2017.1288631. Epub 2017 Feb 28.

Bayesian Nonparametric Ordination for the Analysis of Microbial Communities

Boyu Ren  1 , Sergio Bacallado  2 , Stefano Favaro  3 , Susan Holmes  4 , Lorenzo Trippa  5
Affiliations

Bayesian Nonparametric Ordination for the Analysis of Microbial Communities

Boyu Ren et al. J Am Stat Assoc. 2017.

Abstract

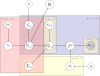
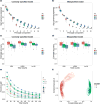
Human microbiome studies use sequencing technologies to measure the abundance of bacterial species or Operational Taxonomic Units (OTUs) in samples of biological material. Typically the data are organized in contingency tables with OTU counts across heterogeneous biological samples. In the microbial ecology community, ordination methods are frequently used to investigate latent factors or clusters that capture and describe variations of OTU counts across biological samples. It remains important to evaluate how uncertainty in estimates of each biological sample's microbial distribution propagates to ordination analyses, including visualization of clusters and projections of biological samples on low dimensional spaces. We propose a Bayesian analysis for dependent distributions to endow frequently used ordinations with estimates of uncertainty. A Bayesian nonparametric prior for dependent normalized random measures is constructed, which is marginally equivalent to the normalized generalized Gamma process, a well-known prior for nonparametric analyses. In our prior, the dependence and similarity between microbial distributions is represented by latent factors that concentrate in a low dimensional space. We use a shrinkage prior to tune the dimensionality of the latent factors. The resulting posterior samples of model parameters can be used to evaluate uncertainty in analyses routinely applied in microbiome studies. Specifically, by combining them with multivariate data analysis techniques we can visualize credible regions in ecological ordination plots. The characteristics of the proposed model are illustrated through a simulation study and applications in two microbiome datasets.

Keywords: Bayesian factor analysis; Dependent Dirichlet processes; Microbiome data analysis; Uncertainty of ordination.

PubMed Disclaimer

Figures

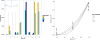
Figure 1
Figure 1
Figure 2
Figure 2
Plate diagram. We include the factor model for the latent variables Qi,j as well as the matrix S. Nodes encompassed by a rectangle are defined over the range of indices indicated at the corner of the rectangle, and the connections shown within the rectangle are between nodes with the same index. We use j to index biological samples, i to index microbial species and l to index the components of latent factors.
Figure 3
Figure 3
(a–b) Estimated proportion of variability captured by the first 10 PCs. Each box-plot here shows the variability of the estimated proportion across 50 simulation replicates. We show the results when the data are generated from the prior (Panel a) and from the model in (13) with a = 1 (Panel b). (c–d) Accuracy of the correlation matrix estimates S^ The box-plots show the variability of the accuracy in 50 simulation replicates, with data generated from the prior (Panel c) and from model (13) with a = 1 (Panel d). We vary the true number of factors m0 (colors) and nj and show the corresponding accuracy variations. (e) Comparison between Bayesian estimates of the underlying microbial distributions Pj and the empirical estimates. We consider the average total variation difference, averaging across all J biological samples. Each curve shows the relationship between nj and average accuracy gain. We set m0 = 3 and the parameter a varies from 0.5 to 3 (shapes). The similarity parameter θ is equal to 0.5, 0.75 or 0.95 (colors). (f) PCoA plot with confidence regions. We visualize the confidence regions using the method in Section 4. Each contour illustrates the uncertainty of a single biological sample’s position. Colors indicate cluster membership and annotated numbers are biological samples’ IDs.
Figure 4
Figure 4
(a) Posterior Probability of each pair of biological samples (j, j′) being clustered together. The labels on axes indicate the environment of origin for each biological sample. (b–d) Ordination plots of biological samples and 95% posterior credible regions. We illustrate the first three compromise axes with three panels. Panel (b) plots projections on the first and second axes. Panel (c) plots projections on the first and third axes. Panel (d) plots projections on the second and third axes. The percentages on the three axes are the ratios of the corresponding S0 eigenvalues and the trace of the matrix. The credible regions for some biological samples are so small that appears as single points. Colors and annotated text indicate the environments.
Figure 5
Figure 5
(a) Posterior Probability of each pair of biological samples (j, j′) being clustered together. The labels on axes indicate the CST for each biological sample. (b–d) Ordination plots of biological samples and posterior credible regions. We illustrate the first three compromise axes with three panels. The percentages on the three axes are the ratios of the corresponding S0 eigenvalues and the trace of the matrix. Colors and indicate CSTs.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abdi H, O’Toole AJ, Valentin D, Edelman B. Computer Vision and Pattern Recognition-Workshops, 2005 CVPR Workshops IEEE Computer Society Conference on. IEEE; 2005. Distatis: The analysis of multiple distance matrices; pp. 42–42.
    1. Anderson MJ, Ellingsen KE, McArdle BH. Multivariate dispersion as a measure of beta diversity. Ecology Letters. 2006;9(6):683–693. - PubMed
    1. Ando T. Bayesian factor analysis with fat-tailed factors and its exact marginal likelihood. Journal of Multivariate Analysis. 2009;100(8):1717–1726.
    1. Bhattacharya A, Dunson DB. Sparse Bayesian infinite factor models. Biometrika. 2011;98(2):291. - PMC - PubMed
    1. Brix A. Generalized gamma measures and shot-noise cox processes. Advances in Applied Probability. 1999:929–953.

Publication types