Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2011 Jun;7(6):e1002042.
doi: 10.1371/journal.pcbi.1002042. Epub 2011 Jun 2.

Effects of heterogeneous and clustered contact patterns on infectious disease dynamics

Erik M Volz  1 , Joel C Miller, Alison Galvani, Lauren Ancel Meyers
Affiliations

Effects of heterogeneous and clustered contact patterns on infectious disease dynamics

Erik M Volz et al. PLoS Comput Biol. 2011 Jun.

Erratum in

  • PLoS Comput Biol. 2011 Jul;7(7). doi: 10.1371/annotation/85b99614-44b4-4052-9195-a77d52dbdc05

Abstract

The spread of infectious diseases fundamentally depends on the pattern of contacts between individuals. Although studies of contact networks have shown that heterogeneity in the number of contacts and the duration of contacts can have far-reaching epidemiological consequences, models often assume that contacts are chosen at random and thereby ignore the sociological, temporal and/or spatial clustering of contacts. Here we investigate the simultaneous effects of heterogeneous and clustered contact patterns on epidemic dynamics. To model population structure, we generalize the configuration model which has a tunable degree distribution (number of contacts per node) and level of clustering (number of three cliques). To model epidemic dynamics for this class of random graph, we derive a tractable, low-dimensional system of ordinary differential equations that accounts for the effects of network structure on the course of the epidemic. We find that the interaction between clustering and the degree distribution is complex. Clustering always slows an epidemic, but simultaneously increasing clustering and the variance of the degree distribution can increase final epidemic size. We also show that bond percolation-based approximations can be highly biased if one incorrectly assumes that infectious periods are homogeneous, and the magnitude of this bias increases with the amount of clustering in the network. We apply this approach to model the high clustering of contacts within households, using contact parameters estimated from survey data of social interactions, and we identify conditions under which network models that do not account for household structure will be biased.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

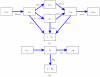
Figure 1
Figure 1. A schematic of the system of equations 7–8.
A: The flux between the probabilities that a node formula image is connected to a triangle with all possible configurations as well as the probability that a node formula image in the triangle has transmitted to formula image. B: The flux between the probabilities that a node formula image is connected by a line to a node formula image that is susceptible, infectious, recovered, and the probability that formula image has transmitted to formula image.
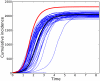
Figure 2
Figure 2. Cumulative number of infections through time.
Fifty stochastic simulations (blue dashed lines) are compared to the solution of equations (black line) 13–17. The degree distribution is generated by equation 29 with formula image and formula image. formula image. For comparison, a trajectory with formula image is shown in red.
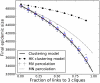
Figure 3
Figure 3. Comparison of clustering models.
The degree distribution is Poisson for the number of pairs of edges (mean degreeformula image). The black line corresponds to the solution of equations 13–17. The boxplots illustrate the 90% confidence interval from 50 stochastic simulations on networks with 5000 nodes. The remaining trajectories correspond to to the original bond percolation calculations , , our modified bond percolation calculations, and the HK clustering model , respectively. formula image.
Figure 4
Figure 4. Epidemic size and bias of network models without clustering.
Left: The final cumulative number of infections as predicted by the clique model is shown as a function of the transmissibility within households and the transmissibility for contacts outside of households. Right: The difference between final epidemic size in a model without clustering and the final size predicted by the clique model.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bansal S, Grenfell B, Meyers L. When individual behaviour matters: homogeneous and network models in epidemiology. J R Soc Interface. 2007;4:879. - PMC - PubMed
    1. Newman M. Spread of epidemic disease on networks. Phys Rev E. 2002;66:16128. - PubMed
    1. Newman M, Strogatz S, Watts D. Random graphs with arbitrary degree distributions and their applications. Phys Rev E. 2001;64:26118. - PubMed
    1. Szendroi B, Csányi G. Polynomial epidemics and clustering in contact networks. Proc R Soc Lond B Biol Sci. 2004;271:S364. - PMC - PubMed
    1. Smieszek T, Fiebig L, Scholz R. Models of epidemics: when contact repetition and clustering should be included. Theor Biol Med Model. 2009;6:11. - PMC - PubMed

Publication types