Abstract
Characterizing the genome-wide dynamic regulation of gene expression is important and will be of much interest in the future. However, there is currently no established method for identifying differentially expressed genes in a time course study. Here we propose a significance method for analyzing time course microarray studies that can be applied to the typical types of comparisons and sampling schemes. This method is applied to two studies on humans. In one study, genes are identified that show differential expression over time in response to in vivo endotoxin administration. By using our method, 7,409 genes are called significant at a 1% false-discovery rate level, whereas several existing approaches fail to identify any genes. In another study, 417 genes are identified at a 10% false-discovery rate level that show expression changing with age in the kidney cortex. Here it is also shown that as many as 47% of the genes change with age in a manner more complex than simple exponential growth or decay. The methodology proposed here has been implemented in the freely distributed and open-source edge software package.
Keywords: aging, differential expression, expression arrays, Q values, time series
The identification of genes that show changes in expression between varying biological conditions is a frequent goal in microarray experiments (1). Differential expression can be studied from a static or temporal viewpoint. In a static experiment, the arrays are obtained irrespective of time, capturing only a single moment of gene expression. In a temporal experiment the arrays are collected over a time course, allowing one to study the dynamic behavior of gene expression. A large amount of work has been done on the problem of identifying differentially expressed genes in static experiments (2). Because the regulation of gene expression is a dynamic process, it is also important to identify and characterize changes in gene expression over time. Here we present a general statistical method that identifies genes differentially expressed over time.
Several clustering methods have been applied to time course microarray data, including hierarchical clustering (3, 4), principal components-based clustering (5), Bayesian model-based clustering (6), and K-means clustering of curves (7, 8). None of these clustering methods is directly applicable to identifying genes that show statistically significant changes in expression over time. The K-means clustering method has been modified to compare expression over time between two groups (9), but this method can only be applied to a few hundred genes at a time because of the computational cost of fitting a single model to all genes simultaneously (7, 8). This approach also requires that the statistical significance be calculated under the assumption that the clustering model estimated for one of the groups is true, which is nonstandard and potentially problematic.
The method that we propose draws on ideas from the extensive statistical literature on time course data analysis (10, 11), particularly spline-based methods (12-16). It is applicable to detecting changes in expression over time within a single biological group and to detecting differences in the behavior of expression over time between two or more groups. Individuals may be sampled at multiple time points, or each time point may represent an independently sampled individual. The computational cost is not substantially greater than methods for static experiments, so there is no impeding limit on the number of genes that may be tested. For example, the method is applied here to microarray studies that each measures ≈40,000 genes.
The proposed method is applied to two recent studies carried out on humans. These studies encompass both types of sampling (longitudinal and independent; discussed below) and both types of differential expression over time (between groups and within a single group). In one study, gene expression was monitored over time in control individuals and endotoxin-treated individuals. Endotoxin [lipopolysaccharide (LPS)] is widely used to study acute inflammatory and immune response; our goal was to understand the mechanism of endotoxin response by identifying genes with expression that is different over time between the treated and untreated groups (17). In a second study, we examined the effect of age on gene expression in the kidney, where samples were obtained from human subjects ranging in age from 27 to 92 years. The goal here was to identify genes whose expression changes significantly with respect to age in human kidney cortex tissue (18). Genes are identified in both studies that corroborate previous findings and provide insights into these problems.
Existing methods for detecting differential expression from static sampling designs (2) are appropriate for comparing unordered categorical conditions, such as three different cancer tumor types (19) or two different treatments (20). It can be shown that these are not generally applicable to time course experiments (see Supporting Appendix, which is published as supporting information on the PNAS web site). Typically these existing methods fail to properly use the temporal structure present in the data, either leading to a loss in power or incorrect calculation of significance. The method that we propose is specifically designed for time course experiments; expression over time is modeled flexibly, and statistical significance is calculated while accounting for sources of dependence over time.
Materials and Methods
Sample Preparations. Details on the protocols are described in refs. 17 and 18. For the endotoxin study, four subjects were administered endotoxin and four were administered a placebo. Blood samples were collected before infusion and at 2, 4, 6, 9, and 24 h afterward. The leukocytes were isolated from the blood samples by using a modified lysis protocol (17). Total RNA was extracted by using an RNeasy kit (Qiagen, Valencia, CA). Samples from hours 4 and 6 were unavailable for one of the controls. For the kidney aging study, samples were obtained from normal kidney tissues removed at nephrectomy or renal transplant biopsy from 74 patients ranging in age from 27 to 92 years. The samples were dissected into cortex and medulla sections based on histological evaluation. Each frozen tissue section was homogenized, and total cellular RNA was isolated according to TRIzol reagent protocol. Comprehensive evaluations were performed and reported elsewhere on various medical factors of the patients (18), and it is unlikely that these factors have confounded age-regulated changes in gene expression (18, 21). Only cortex samples (72 in total) were used in our analysis.
Microarray Analysis. Messenger RNA was amplified and hybridized onto human U133A and U133B GeneChips according to the protocols recommended by Affymetrix (Santa Clara, CA); 44,924 probe sets on the arrays were analyzed. Normalization was performed by using dchip, and expression levels were calculated by using the perfect-match-only model (22). Expression values were then transformed by taking log2(Data + 10), where the relatively negligible number 10 was added to stabilize the variance of values close to zero. The human subjects observed in the kidney aging study did not represent a purely random sample. We attempted to alleviate potential confounding from this sampling scheme by selecting 35,068 probe sets whose expression is well explained by the available sex variable, irrespective of any age-dependent behavior (Supporting Appendix).
Statistical and Computational Details. Thorough details, including formula derivations, algorithms, and theoretical justifications can be found in Supporting Appendix.
Functional Analysis of Significant Genes. Probe sets on Affymetrix U133 GeneChips were mapped to gene IDs. Among the 4,163 probe sets significant at 0.1% for the endotoxin study, 2,914 unique genes were identified from 3,892 probe sets having mapped gene IDs. Among the 417 probe sets significant at 10% for the kidney study, 300 unique genes were identified from 364 probe sets with mapped gene IDs. In both studies, the Ingenuity Pathways Knowledge Base (Ingenuity Systems, Mountain View, CA) was used for functional analysis of genes. Briefly, the Ingenuity Pathways Knowledge Base consists of >106 individually modeled relationships into an ontology of >550,000 biological concepts. Relationships between genes, proteins, small molecules, complexes, cells, processes, and diseases were manually extracted by Ph.D.-level scientists from >200,000 peer-reviewed articles (17).
Results
Experimental Objectives and Statistical Formulations. We developed a general statistical method that identifies genes showing temporal differential expression. This method was applied to two human studies encompassing both types of temporal differential expression.
In one study, kidney cortex samples were obtained from 72 human subjects ranging in age from 27 to 92 years. Only one array was obtained per sample, and the age of the subject was recorded (see Materials and Methods). Fig. 1a displays a simulated example of expression measured from a single gene for this type of study. The solid line is the population average time curve for the probe set, which is its true average expression over time with all sources of variation removed. The points are the observed expression values, one per each individual, and these can be thought of as independent random deviations from the solid line due to biological and measurement variation. “Independent sampling” was performed in this study because each sample of cortex tissue represents an independently sampled individual.
Fig. 1.
Example of independently sampled time course expression data. (a) Simulated example of a gene's expression measurements obtained by independent sampling. The solid line is the population average time curve and the open circles are observed expression values. (b) Expression values of a significant gene in the kidney aging study. The solid line is the curve fit under the alternative hypothesis of differential expression, and the dashed line is the curve fit under the null hypothesis of no differential expression. The × symbols represent observed expression values.
To determine whether each gene has expression that changes with age, our method involves performing a hypothesis test on each gene of whether its population average time curve is flat. We call this type of differential expression “within-class temporal differential expression.” Fig. 1b shows the expression measurements from a highly significant gene, CRABP1, a cellular retinoic acid-binding protein. The gene was tested by first fitting a model under the null hypothesis that there is no differential expression, and then under the alternative hypothesis that there is differential expression. The null model is the dashed flat line that minimizes the sum of squares among all possible flat lines. The alternative model is the solid curve that minimizes the sum of squares among a general class of curves, namely natural cubic splines. A statistic is calculated that compares the goodness of fit of these two models. This statistic is a quantification of evidence for differential expression, and the larger it is the more differentially expressed the gene appears to be. For every gene, a statistic was calculated in this way, and a significance cut-off is applied to them by using a false discovery rate criterion (23). This process involves calculating the null distribution of the statistics when there is no differential expression and is accomplished through a data resampling technique.
In another study, eight human volunteers were randomly divided into endotoxin-treated and control groups of equal size (see Materials and Methods). Fig. 2a is a simulated example of expression measurements from a single gene in a group of four individuals. The solid line is the population average time curve for this gene. The dashed lines are the average time curves for the individuals, meaning that these are the true underlying time curves for each individual with the sources of variation removed up to their individual variation. The deviation of an expression value from its corresponding “individual average time curve” can be thought of as an independent random event. The deviation of an individual average time curve from the population average can also be thought of as an independent random event. However, this implies that the deviations of expression values from the population average time curve are correlated within individuals. The sampling performed in this study is called “longitudinal sampling” because each individual is observed at more than one time point.
Fig. 2.
Example of longitudinally sampled time course expression data. (a) Simulated example of a gene's expression measurements obtained from longitudinal sampling of four individuals. The solid line is the population average time curve. The dashed lines are the average time curves for the individuals. The points of a common shape correspond to one of the individuals. (b) Expression values of a significant gene from the endotoxin study. The solid lines are the curves fit under the alternative hypothesis of differential expression, and the dashed line is the curve fit under the null hypothesis of no differential expression. The × symbols represent controls, and the open circles represent treated individuals.
Here, the goal is to identify genes that show significant differential expression across time between the endotoxin-treated and control groups. We call this type of differential expression “between-class temporal differential expression.” The approach used here is conceptually similar to that in the kidney study. Fig. 2b shows the expression measurements from a significant gene in the study, IFN regulatory factor 1. Under the null hypothesis of no differential expression, the treated and control groups have the same population average time curve. Therefore, a single curve (a natural cubic spline) is fit to the combined groups, which is represented by the dashed curve in Fig. 2b. The alternative model is formed by fitting a separate curve to each group, as is shown by the solid lines in Fig. 2b. A statistic is computed based on the improvement in goodness of fit in going from a single curve to the separate curves for each group. As before, this statistic is a quantification of evidence for differential expression, and the larger it is the more differentially expressed the gene appears to be. A significance cut-off is applied to these statistics in the same fashion as in the kidney aging study.
In contrast to a static experiment, it is more difficult in the time course setting to form statistics that accurately quantify differential expression. Determining the distribution of the statistics when there is no differential expression is also more challenging. The behavior of expression over time may vary greatly from gene to gene, so a flexible modeling approach must be taken in forming statistics. Under certain study designs (e.g., the endotoxin study) there may be dependence between the expression measurements within a single individual, which complicates the formation of statistics and the simulation of the null distribution. Finally, simple permutation methods cannot be used to simulate null statistics because of the complex structure of time course measurements.
Proposed Statistical Method. Methodology was developed to address these issues in a statistically rigorous fashion. In doing so, a general model for gene expression over time within a single biological group was first formulated. Although a single model can be applied to both studies (Supporting Appendix), a simplified version is possible for the kidney study because of its independent sampling scheme. Let yij be the relative expression level of gene i in individual j, where there are i = 1, 2,..., 35,068 probe sets and j = 1, 2,..., 72 individuals. Individual j is observed at age tj, which lies somewhere between 27 and 92 years. The expression values are modeled by
 |
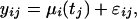where μi(tj) is the population average time curve for gene i evaluated at time tj and where εij is the random deviation from this curve. In terms of Fig. 1a, μi(t) is shown by the solid line. The distance between this curve and an observed expression value is εij. The εij are assumed to be independent random variables with mean zero and gene-dependent variance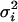 
.
The following model was developed for the endotoxin study and for longitudinal sampling in general. Let yijk be the relative expression level of gene i on individual j at the kth time point, where there are i = 1, 2,..., 44,924 probe sets and j = 1, 2,..., 8 different individuals sampled (four within each group). For each individual, there were k = 1, 2,..., 6 time points observed at times tjk, except for the one control, who is missing two time points. The expression values are modeled by
 |
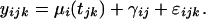The population average time curve for gene i is again μi(t). Individual j deviates from μi(t) by γij, implying that μi(t) + γij is the individual average time curve for individual j. The measurement error and remaining sources of random variation are modeled by εijk. The solid line in Fig. 2a is represented by μi(t), and the dashed lines are represented by μi(t) + γij. Each expression value deviates from its corresponding dashed line by εijk. The γij and εijk are assumed to be independent random variables with means equal to zero and gene-dependent variances 
and 
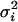, respectively. The case for which γij is modeled as a curve will be dealt with elsewhere; however, the endotoxin study did not contain enough observations to permit this extra level of complexity.
The population average time curve μi(t) is parameterized in terms of an intercept plus a p-dimensional linear basis:
 |
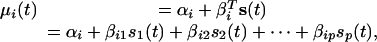where s(t) = [s1(t), s2(t),..., sp(t)]T is a prespecified p-dimensional basis, αi is the unknown gene-specific intercept, and βi = [βi1, βi2,..., βip]T is a p-dimensional vector of unknown gene-specific parameters. A natural choice for the basis is a polynomial of degree p, which would result in modeling μi(t) = αi + βi1t + βi2t2 + ··· + βiptp. The polynomial basis was effective in both studies, although a natural cubic spline basis is more flexible and makes fewer assumptions (12-16). Furthermore, a natural cubic spline parameterization of μi(t) resulted in increased power in both studies. For either type of basis, the curve was estimated by minimizing the sum of squares between the curve and the observed expression values, which involves assigning values to only αi and βi. The model fitting procedure for longitudinal sampling is slightly more complicated in that it also takes into account the dependence of measurements within an individual (Supporting Appendix). We also developed a method to automatically choose a single value of the basis dimension p for all genes based on a singular value decomposition of the expression data (Supporting Appendix). We found that allowing p to vary from gene to gene or choosing a single p in a post hoc fashion lead to anticonservative inflation of significance due to overfitting.
Not only does the basis representation of μi(t) facilitate model fitting, but it also greatly simplifies the hypothesis tests for differential expression. The tests can now be written in terms of the αi and βi for each gene, which implies that the tests do not depend on specific time points, so general sampling schemes may be analyzed as we have claimed. In the kidney aging study, the null hypothesis of no differential expression is equivalent to restricting μi(t) to be a constant, and the alternative hypothesis of differential expression allows μi(t) to be a curve. Thus, the null hypothesis model is fit under the constraint that μi(t) = αi and βi = 0, and the alternative hypothesis model is fit under the general parametrization of μi(t). For the endotoxin study, the null hypothesis is that the treated and control groups have equal μi(t) (i.e., equal αi and βi), and the alternative hypothesis is that they are not equal. The null hypothesis model is obtained by fitting a curve to the two groups combined, and the alternative hypothesis model is obtained by fitting a separate curve to each group. In this particular study, we were not interested in a difference in the intercepts αi because all individuals started out as untreated at time 0. Therefore, the intercept was implicitly assumed to be equal between the two groups under both hypotheses, which comes down to a test for equality of the βi between the two groups. This equality will not always be the case when testing for between-class temporal differential expression, so we have developed model fitting methods for both scenarios (Supporting Appendix).
A statistic for each gene was then formed that quantifies differential expression. The statistic was defined to be an analogue of the t and F statistics that are commonly used in static differential expression methods. The statistic compares the goodness of fit of the model under the null hypothesis to that under the alternative hypothesis. First, fitted values from the null and alternative models are calculated for each observed value. The residuals of the model fits are then obtained by subtracting the fitted from the observed values. Calculating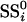 
to be the sum of squares of the residuals obtained from the null model, and 
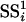from the alternative model, the statistic for gene i was constructed as
 |
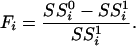This statistic is proportional to the typical F statistic used in comparing two nested models. The intuition behind the formula is that 
quantifies the increase in goodness of fit, and dividing this difference by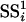 
provides exchangeability of the Fi across the genes. Justification and exact formulas for all cases can be found in Supporting Appendix.
The null distribution of these statistics is calculated through a data resampling method called the bootstrap (24), where residuals from the alternative model are resampled and added back to the null model to simulate the case where there is no differential expression (Supporting Appendix). We note that our resampling scheme takes into account dependence between time points when the study involves longitudinal sampling. The observed statistics and null statistics were used to estimate a Q value for each gene (Supporting Appendix), which estimates the false-discovery rate incurred when calling the gene significant (23, 25).
Analysis of Systemic Inflammatory Response Induced by LPS. In the endotoxin study there are 4,163, 7,409, and 12,720 significant probe sets at respective Q-value cut-offs of 0.1%, 1%, and 5%. These results indicate that an endotoxin injection causes a profound gene expression response in blood leukocytes, which is expected for a number of reasons. First, in vivo administration of LPS invokes an acute systemic inflammation that dramatically perturbs the body's physiology. Second, some differential expression may be due to changing distributions of cell populations in the blood in addition to transcriptional changes (17). Also, measuring differential expression over time is a more sensitive study design than the typical static design; any change over time qualifies as differential expression. A t test (23) and the sam software (20, 23) were used to test for differential expression between 0 and 2 h and between 0 and 4 h. The significance results are displayed in Table 1, where it can be seen that an actual time course analysis offers a sizeable increase in statistical power over a static design analysis.
Table 1. A comparison of the number of probe sets called significant as found by the proposed method, a standard t test, and a sam test.
| Proposed method
|
||||||
|---|---|---|---|---|---|---|
| Eight subjects, 46 arrays
|
Four subjects, 16 arrays
|
t test
|
sam
|
|||
| Q value cutoff, % | 0 h vs. 2 h | 0 h vs. 4 h | 0 h vs. 2 h | 0 h vs. 4 h | ||
| 1 | 7,409 | 548 | 0 | 0 | 0 | 0 |
| 2 | 9,188 | 2,683 | 226 | 91 | 65 | 0 |
| 3 | 10,467 | 4,392 | 1,678 | 837 | 1,756 | 695 |
| 4 | 11,642 | 5,859 | 2,524 | 1,826 | 2,535 | 1,718 |
| 5 | 12,720 | 7,229 | 3,202 | 2,686 | 3,101 | 2,694 |
Shown is a comparison of the proposed method to a standard t test and a sam test, which is a t test with adaptive asymmetric thresholding. The ratio of the number of probe sets called significant is an estimate of the increase in power that our procedure provides. For the static methods, eight subjects and 16 arrays were used to compare two time points (0 h vs. 2 h and 0 h vs. 4 h). The proposed method was compared to the static methods in two ways. First, all 8 subjects and 46 arrays were used, potentially giving our method an advantage due to a decrease in technical replication variance. Second, only four subjects were used at times 0, 4, 6, and 24 h for a total of 16 arrays, giving the static methods a substantial advantage in that they have twice as many biological replicates. The fairest comparison lies in between these two, although both applications outperform the static methods substantially.
Under the assumption that the control individuals have flat expression over time, it would have sufficed to simply test the endotoxin individuals for within-class temporal differential expression. However, we found that, among the controls, at least 6% of the probe sets show within-class temporal differential expression. We also tested the endotoxin-treated individuals for within-class temporal differential expression and found the significance to be inflated to unrealistic levels. Therefore, it is necessary to include both treated and control individuals in a test for between-class temporal differential expression to identify genes differentially expressed because of LPS injection.
To get a broad picture of the behavior of differentially expressed genes, a singular value decomposition was performed on the 4,163 most significant probe sets. Fig. 3 shows the top two eigen-genes that explain 66% and 16% of the variance, respectively. The relevant information is the shape of each eigen-gene, not the magnitude or direction of differential expression. Among the 4,163 most significant probe sets, 27% are up-regulated as the eigen-gene is drawn; 73% are down-regulated, which is simply the reflection of the eigen-gene's shape across the time axis. The second eigen-gene shows more complex behavior, where changes in expression occur in both directions over the time course. We identified 2,914 unique genes among the 4,136 probe sets; 756 showed up-regulation during the time course, and 2,158 showed down-regulation. Global functional analysis was performed by using a gene ontology built from experimental evidence compiled in the Ingenuity Pathways Knowledge Base (Fig. 4 and Data Set 1, which is published as supporting information on the PNAS web site).
Fig. 3.
Smoothed version of the top two eigen-genes obtained from probe sets significant at Q ≤ 0.1% in the endotoxin study. The solid lines are smoothers fit to endotoxin-treated individuals, and the dashed lines are fit to the control individuals. The first eigen-gene explains 66% of the variance and is represented by the black lines. The second eigen-gene explains 16% of the variance and is represented by the gray lines.
Fig. 4.
Functional analysis of genes found to be significant at Q ≤ 0.1% in the endotoxin study. Shown are representative functions differentially enriched [difference in log(significance) > 4] between the groups of up-regulated (light gray) and down-regulated (black) genes. The significance values of these functions in the combined group are shown in dark gray.
The most significant functional groups from the 756 up-regulated genes take part in immune response (121 genes), inflammatory disease (41 genes), cellular movement (84 genes), tissue morphology (72 genes), and cell death (144 genes). These groups are consistent with an intense response of leukocytes to LPS. The apparent expression of many elements of inflammation are up-regulated, including secretive cytokines, chemokines, and associated proteins (CCL20, CCL3, CCL4, CXCL16, CXCL2, IL-1A, IL-1B, IL-8, TNF, TNF-SF13B, IL-1RAP, IL-1RN, TNF-AIP3, and TNF-AIP6); their membrane receptors (CCR1, IL-10RB, IL-18R1, IL-18RAP, IL-1R1, IL-1R2, IL-4R, IL-8RA, IL-9R, and TNF-RSF6), Toll-like receptors (TLR4, TLR5, TLR6, and TLR8), Fc receptors (FC-AR, FC-ER1G, FC-GR1A, FC-GR2A, and FC-GR2B), IFN receptors (IFN-GR1, IFN-GR2, and IFN-AR1), protein tyrosine phosphatases (PTP-4A1, PTP-N2, PTP-N22, PTP-NS1, PTP-RC, PTP-RJ, PTP-RN2, and PTP-RO), Janus tyrosine kinases/signal transducers and activators of transcription (JAK2, JAK3, STAT2, STAT3, STAT5A, and STAT5B), and NFκB/IKB proteins (NFκB-2, NFκB-IA, and NFκB-IE). These and other elevated genes participate in the activation of innate immune response and many functions of leukocytes, including cell movement of leukocytes, infiltration, migration, phagocytosis, activation, chemotaxis, proliferation, and recruitment. The most significantly up-regulated gene is ORM1, a key acute phase plasma protein.
The most significant functional groups from the genes showing down-regulation are protein synthesis (83 genes), including genes of elongation initiation factors, ribosomal proteins, mitochondrial ribosomal protein; and RNA posttranscriptional modification (60 genes), including genes such as heterogeneous nuclear ribonucleoproteins, small nuclear ribonucleoproteins, and splicing factors. Members of RNA polymerase II are also decreased. Correspondingly, genes involved in oxidative phosphorylation, such as mitochondrial complexes I (NDUF), II (SDH), III (UQCR), and IV (COX) are down-regulated. This concerted suppression of the cell's protein syntheses, transcription programs, and energy productions may reflect a generalized stress response in blood leukocytes. Interestingly, expression levels of members associated with the MHC class II are also suppressed, consistent with the reduced antigen-presenting capability after LPS shock.
Taking these results together, we observed a comprehensive transcriptional response to LPS stimulation, where leukocyte cells reallocate resources and up-regulate transcription of genes involved in innate immune and defense mechanisms.
Analysis of Age-Related Genes in the Kidney Cortex. We detected substantial differential expression in this study, although not nearly as much as in the previous study. At Q-value cutoffs of 5% and 10%, there are 187 and 436 significant probe sets, respectively. Among the 436 probe sets significant at Q ≤ 10%, 320 unique genes were identified, with 240 show increasing expression with age and 80 show decreasing expression.
A functional analysis was also performed on these age-regulated genes (Data Set 2, which is published as supporting information on the PNAS web site). The most significant functional group is immune response (69 genes), which includes genes associated with the complement component (C1QA, C1QB, C1QG, C1QR1, C1R, C1S, and C4A), cytokines, chemokines, and receptors (CCL2, CCL20, CCR1, CX3CR1, CXCL9, CXCR4, IL10RB, CSF1R, and CSF2RB), and the MHC II complex (FCER1G, HLA-DMA, HLA-DPA1, HLA-DQB1, HLA-DRB1, and HLA-DRB3). All but three of these genes show up-regulated expression with age, which suggests an increased abundance of immune response genes in the kidney cortex, perhaps as a result of a low level of inflammation over life or as a compensation for the decreased immune function in older age. Renal infiltration with immunocompetent cells, which is known to correlate with renal diseases and increase over age, can also account for some of these observed changes.
The aging process has previously been shown to involve a widespread and complicated alteration in gene expression (18). In our analysis, significant genes were identified that have a variety of cell-to-cell signaling and interaction (68 genes). For example, 34 genes are involved in the quantity or mobilization of calcium and 14 genes in tyrosine phosphorylation. Fifty-nine genes were identified to be involved in apoptosis and cell death. The expression levels of apoptosis-enhancer proteins MYC (C-MYC), SP1 (Sp1 transcription factor), caspase 1, and ubiquitin D increase with age in the kidney, whereas the antiapoptosis protein HSPA9B (mortalin-2) decreases with age. However, the expression of BCL2A1, an inhibitor of the intrinsic apoptosis pathway, is observed to be increasing with age (26).
Gene expression may change with age in response to declining kidney function and increased susceptibility to kidney disease. Interestingly, a group of 12 genes known to be localized in mitochondria (HSPA9B, COX8A, COX7C, AKAP1, BCKDHA, CLPP, FDX1, AMT, DBT, ATP5G3, AK2, and NME4) are identified as significant, and their expression level uniformly declines in older age. A number of age-regulated genes are also known to be involved in renal diseases, including C1QA, CCR1, LYN, PTPRC, and TNFSF13B, which all show increasing expression with age (27-31). The expression of TRPM6 (a transient receptor potential cation channel) negatively correlates with age, and mutations of this gene cause hypomagnesemia with secondary hypocalcemia (32).
We used a 4-dimensional basis in the significance analysis, although other choices of p are possible. A 1-dimensional basis is equivalent to identifying differential expression by fitting a linear regression and testing whether the slope is zero. Applied to log-transformed expression data, a linear regression is only able to identify genes that show simple exponential behavior in their differential expression. By testing the null hypothesis of linear or flat log-transformed expression, we found that at least 25% of the 35,068 probe sets are differentially expressed in a manner more complex than an exponential function of age. Among the 417 most significant probe sets when using the 1-dimensional basis, it is estimated that at least 47% of these are more complex than simple exponential behavior. At Q ≤ 5%, just over half of the genes found to be significant using the 4-dimensional basis are also significant when using the 1-dimensional basis. Therefore, there is potentially a functional class of genes showing simple exponential temporal differential expression and another functional class showing substantially more complex differential expression.
Discussion
We have proposed a significance method to identify differentially expressed genes in time course microarray experiments and applied it to studies involving two types of sampling and both types of temporal differential expression. The method may also be applied to more complicated situations, where three or more groups are compared, for example. We have justified the method in terms of well established statistical concepts (Supporting Appendix).
Temporally differentially expressed genes were identified in two time course microarray studies on humans. The human in vivo model of bacterial endotoxin represents a unique opportunity to examine the onset of systemic inflammation in blood leukocytes. Our analysis suggests that a genome-wide transcriptional response takes place where blood leukocytes reallocate resources and up-regulate transcription of genes involved in innate immune and defense mechanisms. The inclusion of controls in this study played an important role, in which the controls themselves showed differential expression over time. In the clinical setting, comparing a treatment group to time 0 does not provide a proper control over the entire time course. The significance analysis of the kidney aging study indicates that a large proportion of genes have expression that increases with age, including those involved in signal transduction, cell growth, and genome stability. Genes related to metabolism were found to be decreasing with age. It was also shown that a large proportion of gene expression changing with age does so in a manner more complex than exponential growth. Therefore, in general it is important to use flexible models when identifying genes that are temporally differentially expressed.
We have developed a freely available point-and-click software package called edge that includes this methodology and new methodology for static experiments. edge is available from J.D.S. upon request.
Supplementary Material
Acknowledgments
We thank Stuart Kim, Steve Calvano, and Stephen Lowry for generously sharing data and James Dai for helping with the calculations used for Table 1. This research was supported by National Institutes of Health Grant R01 HG002913-01 (to J.D.S.) and National Institutes of Health Large-Scale Collaborative Research Grant U54 GM2119-03¶ (principle investigator, R.G.T.).
Author contributions: J.D.S., W.X., R.G.T., and R.W.D. designed research; J.D.S., W.X., and J.T.L. performed research; J.D.S., W.X., and J.T.L. contributed new reagents/analytic tools; J.D.S., W.X., and J.T.L. analyzed data; and J.D.S. and W.X. wrote the paper.
Abbreviation: LPS, lipopolysaccharide.
Footnotes
Participating investigators: H. V. Baker, P. E. Bankey, T. R. Billiar, B. H. Brownstein, S. E. Calvano, I. H. Chaudry, J. P. Cobb, C. Cooper, B. Freeman, R. L. Gamelli, N. S. Gibran, B. G. Harbrecht, W. Heagy, D. M. Heimbach, D. N. Herndon, J. W. Horton, J. L. Hunt, J. Johnson, J. A. Lederer, T. Logvinenko, S. F. Lowry, J. A. Mannick, B. A. McKinley, C. Miller-Graziano, M. N. Mindrinos, J. P. Minei, L. L. Moldawer, E. E. Moore, F. A. Moore, A. B. Nathens, G. E. O'Keefe, L. G. Rahme, D. G. Remick, Jr., M. B. Shapiro, R. L. Sheridan, G. M. Silver, R. D. Smith, S. Somers, G. Stephanopoulos, M. Toner, H. S. Warren, M. A. West, S. E. Wolf, and V. R. Young.
References
- 1.Slonim, D. K. (2002) Nat. Genet. 32, 502-508. [DOI] [PubMed] [Google Scholar]
- 2.Cui, X. & Churchill, G. A. (2003) Genome Biol. 4, 210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eisen, M. B., Spellman, P. T., Brown, P. O. & Botstein, D. (1998) Proc. Natl. Acad. Sci. USA 95, 14863-14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhu, G., Spellman, P. T., Volpe, T., Brown, P. O., Botstein, D., Davis, T. N. & Futcher, B. (2000) Nature 406, 90-94. [DOI] [PubMed] [Google Scholar]
- 5.Alter, O., Brown, P. O. & Botstein, D. (2000) Proc. Natl. Acad. Sci. USA 97, 10101-10106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wakefield, J., Zhou, C. & Self, S. (2003) Bayesian Stat. 7, 721-732. [Google Scholar]
- 7.Bar-Joseph, Z., Gerber, G., Jaakkola, T. S., Gifford, D. K. & Simon, I. (2003) J. Comp. Bio. 10, 341-356. [DOI] [PubMed] [Google Scholar]
- 8.Luan, Y. & Li, H. (2003) Bioinformatics 19, 474-482. [DOI] [PubMed] [Google Scholar]
- 9.Bar-Joseph, Z., Gerber, G., Simon, I., Gifford, D. K. & Jaakkola, T. S. (2003) Proc. Natl. Acad. Sci. USA 100, 10146-10151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Diggle, P., Heagerty, P., Liang, K. Y. & Zeger, S. (2002) Analysis of Longitudinal Data (Oxford Univ. Press, Oxford), 2nd Ed.
- 11.Ramsay, J. O. & Silverman, B. W. (1997) Functional Data Analysis (Springer, Berlin).
- 12.Wang, Y. (1998) J. R. Stat. Soc. B 60, 159-174. [Google Scholar]
- 13.James, G. & Hastie, T. (2001) J. R. Stat. Soc. B 63, 533-550. [Google Scholar]
- 14.Rice, J. & Wu, C. (2001) Biometrics 57, 253-259. [DOI] [PubMed] [Google Scholar]
- 15.Irizarry, R. A., Tankersley, C. G., Frank, R. & Flanders, S. E. (2001) Biometrics 57, 1228-1237. [DOI] [PubMed] [Google Scholar]
- 16.James, G. & Sugar, C. (2003) J. Am. Stat. Assoc. 98, 397-408. [Google Scholar]
- 17.Calvano, S. E., Xiao, W., Richards, D. R., Felciano, R. M., Baker, H. V., Cho, R. J., Chen, R. O., Brownstein, B. H., Cobb, J. P., Tschoeke, S. K., et al. (2005) Nature, in press. [DOI] [PubMed]
- 18.Rodwell, G. E. J., Sonu, R., Zahn, J. M., Lund, J., Wilhelmy, J., Wang, L., Xiao, W., Mindrinos, M., Crane, E., Segal, E., et al. (2004) PLoS Biol. 2, e427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hedenfalk, I., Duggan, D., Chen, Y. D., Radmacher, M., Bittner, M., Simon, R., Meltzer, P., Gusterson, B., Esteller, M., Kallioniemi, O. P., et al. (2001) N. Engl. J. Med. 344, 539-548. [DOI] [PubMed] [Google Scholar]
- 20.Tusher, V., Tibshirani, R. & Chu, C. (2001) Proc. Natl. Acad. Sci. USA 98, 5116-5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Higgins, J., Wang, L., Kambham, N., Montgomery, K., Maxon, V., Vogelmann, S., Lemley, K., Brown, P., Brooks, J. & van de Rijn, M. (2004) Mol. Biol. Cell 15, 649-656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li, C. & Wong, W. H. (2001) Proc. Natl. Acad. Sci. USA 98, 31-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Storey, J. D. & Tibshirani, R. (2003) Proc. Natl. Acad. Sci. USA 100, 9440-9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Efron, B. & Tibshirani, R. J. (1993) An Introduction to the Bootstrap (Chapman & Hall, Boca Raton, FL).
- 25.Storey, J. D. (2002) J. R. Stat. Soc. B 64, 479-498. [Google Scholar]
- 26.Hipfner, D. & Cohen, S. (2004) Nat. Rev. Mol. Cell Biol. 5, 805-816. [DOI] [PubMed] [Google Scholar]
- 27.Yu, C., Yen, T., Lowell, C. & DeFranco, A. (2001) Curr. Biol. 11, 34-38. [DOI] [PubMed] [Google Scholar]
- 28.Majeti, R., Xu, Z., Parslow, T., Olson, J., Daikh, D., Killeen, N. & Weiss, A. (2000) Cell 103, 1059-1070. [DOI] [PubMed] [Google Scholar]
- 29.Mitchell, D., Pickering, M., Warren, J., Fossati-Jimack, L., Cortes-Hernandez, J., Cook, H., Botto, M. & Walport, M. (2002) J. Immunol. 168, 2538-2543. [DOI] [PubMed] [Google Scholar]
- 30.Topham, P., Csizmadia, V., Soler, D., Hines, D., Gerard, C., Salant, D. & Hancock, W. (1999) J. Clin. Invest. 104, 1549-1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gross, J., Johston, J., Mudri, S., Enselman, R., Dillon, S., Madden, K., Xu, W., Parrish-Novak, J., Foster, D., Lofton-Day, C., et al. (2000) Nature 404, 995-999. [DOI] [PubMed] [Google Scholar]
- 32.Schilingmann, K., Weber, S., Peters, M., Niemann Nejsum, L., Vitzthum, H., Klingel, K., Kratz, M., Haddad, E., Ristoff, E., Dinour, D., et al. (2002) Nat. Genet. 31, 166-170. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.