Deployment & Documentation & Stats & License
Background: Outlier detection (OD) is a key data mining task for identifying abnormal objects from general samples with numerous high-stake applications including fraud detection and intrusion detection.
We propose TOD, a system for efficient and scalable outlier detection (OD) on distributed multi-GPU machines. A key idea behind TOD is decomposing OD applications into basic tensor algebra operations for GPU acceleration.
Citing TOD: Check out the design paper. If you use TOD in a scientific publication, we would appreciate citations to the following paper:
@article{zhao2021tod,
title={TOD: GPU-accelerated Outlier Detection via Tensor Operations},
author={Zhao, Yue and Chen, George H and Jia, Zhihao},
journal={arXiv preprint arXiv:2110.14007},
year={2021}
}
or:
Zhao, Y., Chen, G.H. and Jia, Z., 2021. TOD: GPU-accelerated Outlier Detection via Tensor Operations. arXiv preprint arXiv:2110.14007.
On average, TOD is 11 times faster than PyOD on a diverse group of OD algorithms!
If you need another reason: it can handle much larger datasets---more than a million sample OD within an hour!
GPU-accelerated Outlier Detection with 5 Lines of Code:
# train the COPOD detector
from pytod.models.knn import KNN
clf = KNN() # default GPU device is used
clf.fit(X_train)
# get outlier scores
y_train_scores = clf.decision_scores_ # raw outlier scores on the train data
y_test_scores = clf.decision_function(X_test) # predict raw outlier scores on testTOD is featured for:
- Unified APIs, detailed documentation, and examples for the easy use (under construction)
- More than 5 different OD algorithms and more are being added
- The support of multi-GPU acceleration
- Advanced techniques including provable quantization and automatic batching
Table of Contents:
- Installation
- Implemented Algorithms
- A Motivating Example PyOD vs. PyTOD
- Paper Reproducibility
- Programming Model Interface
- End-to-end Performance Comparison with PyOD
It is recommended to use pip for installation. Please make sure the latest version is installed, as PyTOD is updated frequently:
pip install pytod # normal install
pip install --upgrade pytod # or update if neededAlternatively, you could clone and run setup.py file:
git clone https://github.com/yzhao062/pytod.git
cd pyod
pip install .Required Dependencies:
- Python 3.6+
- mpmath
- numpy>=1.13
- torch>=1.7 (it is safer if you install by yourself)
- scipy>=0.19.1
- scikit_learn>=0.21
- pyod>=1.0.4 (for comparison)
PyTOD toolkit consists of three major functional groups (to be cleaned up):
(i) Individual Detection Algorithms :
| Type | Abbr | Algorithm | Year | Ref |
|---|---|---|---|---|
| Linear Model | PCA | Principal Component Analysis (the sum of weighted projected distances to the eigenvector hyperplanes) | 2003 | [29] |
| Proximity-Based | LOF | Local Outlier Factor | 2000 | [7] |
| Proximity-Based | COF | Connectivity-Based Outlier Factor | 2002 | [30] |
| Proximity-Based | HBOS | Histogram-based Outlier Score | 2012 | [9] |
| Proximity-Based | kNN | k Nearest Neighbors (use the distance to the kth nearest neighbor as the outlier score) | 2000 | [25] |
| Proximity-Based | AvgKNN | Average kNN (use the average distance to k nearest neighbors as the outlier score) | 2002 | [5] |
| Proximity-Based | MedKNN | Median kNN (use the median distance to k nearest neighbors as the outlier score) | 2002 | [5] |
| Probabilistic | ABOD | Angle-Based Outlier Detection | 2008 | [16] |
| Probabilistic | COPOD | COPOD: Copula-Based Outlier Detection | 2020 | [20] |
| Probabilistic | FastABOD | Fast Angle-Based Outlier Detection using approximation | 2008 | [16] |
Code is being released. Watch and star for the latest news!
kNN example shows that how fast and how easy PyTOD is. Take the famous kNN outlier detection as an example:
Initialize a kNN detector, fit the model, and make the prediction.
from pytod.models.knn import KNN # kNN detector # train kNN detector clf_name = 'KNN' clf = KNN() clf.fit(X_train)
# if GPU is not available, use CPU instead clf = KNN(device='cpu') clf.fit(X_train)
Get the prediction results
# get the prediction label and outlier scores of the training data y_train_pred = clf.labels_ # binary labels (0: inliers, 1: outliers) y_train_scores = clf.decision_scores_ # raw outlier scores
On a simple laptop, let us see how fast it is in comparison to PyOD for 30,000 samples with 20 features
KNN-PyOD ROC:1.0, precision @ rank n:1.0 Execution time 11.26 seconds
KNN-PyTOD-GPU ROC:1.0, precision @ rank n:1.0 Execution time 2.82 seconds
KNN-PyTOD-CPU ROC:1.0, precision @ rank n:1.0 Execution time 3.36 seconds
It is easy to see, PyTOD shows both better efficiency than PyOD.
Datasets: OD benchmark datasets are available at datasets folder.
Scripts for reproducibility is available in reproducibility folder.
Cleanup is on the way!
Complex OD algorithms can be abstracted into common tensor operators.
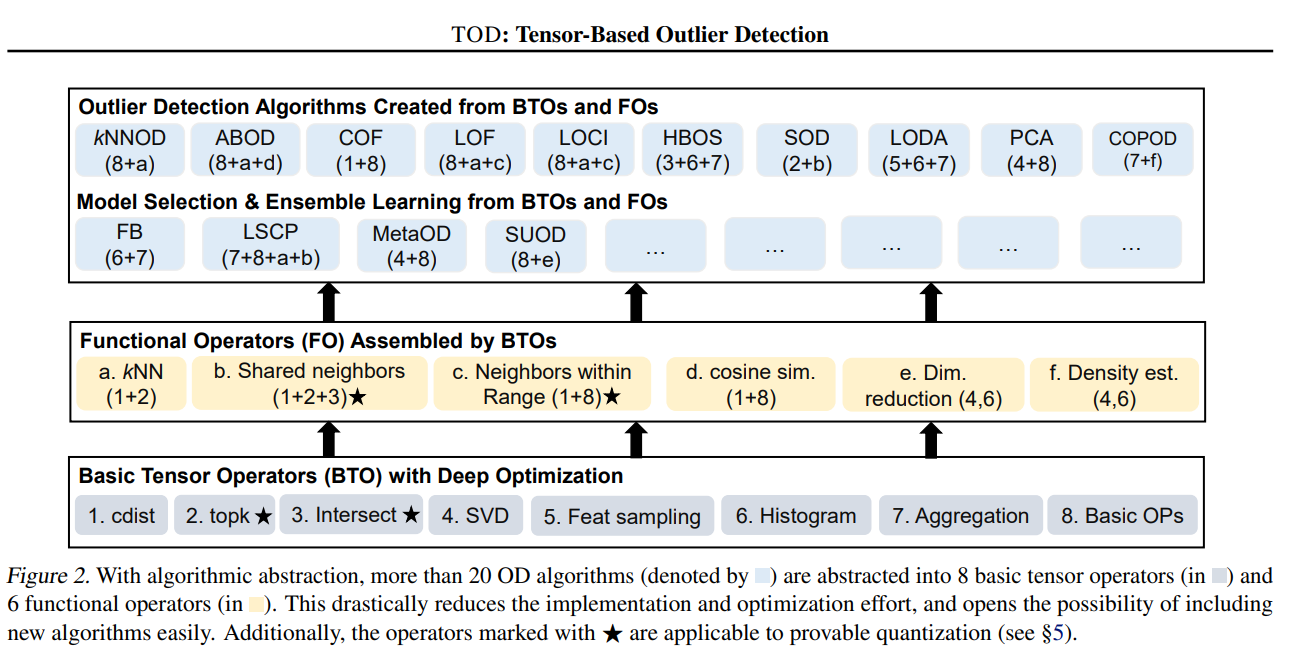
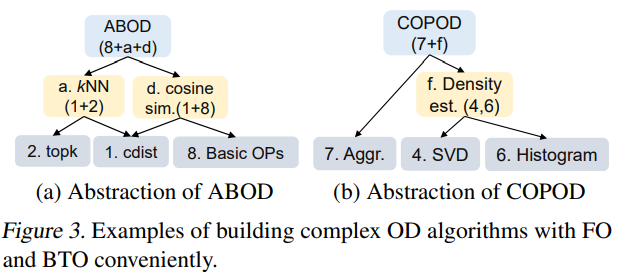
For instance, ABOD and COPOD can be assembled by the basic tensor operators.
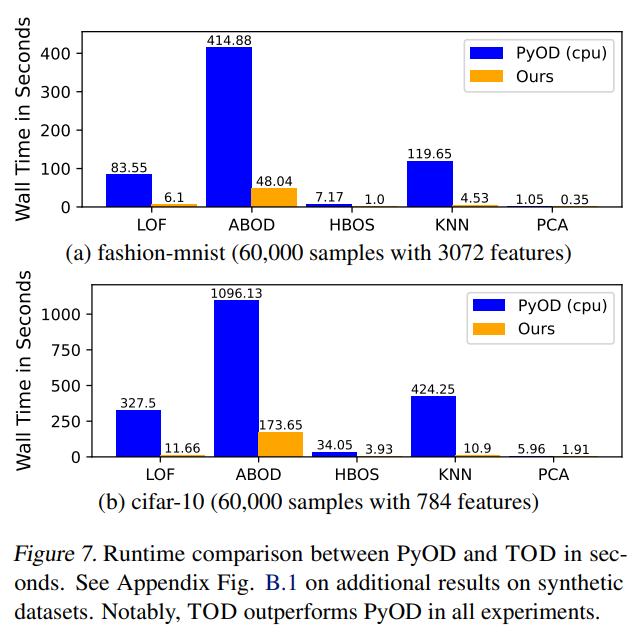
Overall, it is much (on avg. 11 times) faster than PyOD takes way less run time.
| [1] | Aggarwal, C.C., 2015. Outlier analysis. In Data mining (pp. 237-263). Springer, Cham. |
| [2] | Aggarwal, C.C. and Sathe, S., 2015. Theoretical foundations and algorithms for outlier ensembles.ACM SIGKDD Explorations Newsletter, 17(1), pp.24-47. |
| [3] | Aggarwal, C.C. and Sathe, S., 2017. Outlier ensembles: An introduction. Springer. |
| [4] | Almardeny, Y., Boujnah, N. and Cleary, F., 2020. A Novel Outlier Detection Method for Multivariate Data. IEEE Transactions on Knowledge and Data Engineering. |
| [5] | (1, 2) Angiulli, F. and Pizzuti, C., 2002, August. Fast outlier detection in high dimensional spaces. In European Conference on Principles of Data Mining and Knowledge Discovery pp. 15-27. |
| [6] | Arning, A., Agrawal, R. and Raghavan, P., 1996, August. A Linear Method for Deviation Detection in Large Databases. In KDD (Vol. 1141, No. 50, pp. 972-981). |
| [7] | Breunig, M.M., Kriegel, H.P., Ng, R.T. and Sander, J., 2000, May. LOF: identifying density-based local outliers. ACM Sigmod Record, 29(2), pp. 93-104. |
| [8] | Burgess, Christopher P., et al. "Understanding disentangling in beta-VAE." arXiv preprint arXiv:1804.03599 (2018). |
| [9] | Goldstein, M. and Dengel, A., 2012. Histogram-based outlier score (hbos): A fast unsupervised anomaly detection algorithm. In KI-2012: Poster and Demo Track, pp.59-63. |
| [10] | Gopalan, P., Sharan, V. and Wieder, U., 2019. PIDForest: Anomaly Detection via Partial Identification. In Advances in Neural Information Processing Systems, pp. 15783-15793. |
| [11] | Hardin, J. and Rocke, D.M., 2004. Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator. Computational Statistics & Data Analysis, 44(4), pp.625-638. |
| [12] | He, Z., Xu, X. and Deng, S., 2003. Discovering cluster-based local outliers. Pattern Recognition Letters, 24(9-10), pp.1641-1650. |
| [13] | Iglewicz, B. and Hoaglin, D.C., 1993. How to detect and handle outliers (Vol. 16). Asq Press. |
| [14] | Janssens, J.H.M., Huszár, F., Postma, E.O. and van den Herik, H.J., 2012. Stochastic outlier selection. Technical report TiCC TR 2012-001, Tilburg University, Tilburg Center for Cognition and Communication, Tilburg, The Netherlands. |
| [15] | Kingma, D.P. and Welling, M., 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114. |
| [16] | (1, 2) Kriegel, H.P. and Zimek, A., 2008, August. Angle-based outlier detection in high-dimensional data. In KDD '08, pp. 444-452. ACM. |
| [17] | Kriegel, H.P., Kröger, P., Schubert, E. and Zimek, A., 2009, April. Outlier detection in axis-parallel subspaces of high dimensional data. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 831-838. Springer, Berlin, Heidelberg. |
| [18] | Lazarevic, A. and Kumar, V., 2005, August. Feature bagging for outlier detection. In KDD '05. 2005. |
| [19] | Li, D., Chen, D., Jin, B., Shi, L., Goh, J. and Ng, S.K., 2019, September. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In International Conference on Artificial Neural Networks (pp. 703-716). Springer, Cham. |
| [20] | Li, Z., Zhao, Y., Botta, N., Ionescu, C. and Hu, X. COPOD: Copula-Based Outlier Detection. IEEE International Conference on Data Mining (ICDM), 2020. |
| [21] | Liu, F.T., Ting, K.M. and Zhou, Z.H., 2008, December. Isolation forest. In International Conference on Data Mining, pp. 413-422. IEEE. |
| [22] | Liu, Y., Li, Z., Zhou, C., Jiang, Y., Sun, J., Wang, M. and He, X., 2019. Generative adversarial active learning for unsupervised outlier detection. IEEE Transactions on Knowledge and Data Engineering. |
| [23] | Papadimitriou, S., Kitagawa, H., Gibbons, P.B. and Faloutsos, C., 2003, March. LOCI: Fast outlier detection using the local correlation integral. In ICDE '03, pp. 315-326. IEEE. |
| [24] | Pevný, T., 2016. Loda: Lightweight on-line detector of anomalies. Machine Learning, 102(2), pp.275-304. |
| [25] | Ramaswamy, S., Rastogi, R. and Shim, K., 2000, May. Efficient algorithms for mining outliers from large data sets. ACM Sigmod Record, 29(2), pp. 427-438. |
| [26] | Rousseeuw, P.J. and Driessen, K.V., 1999. A fast algorithm for the minimum covariance determinant estimator. Technometrics, 41(3), pp.212-223. |
| [27] | Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Siddiqui, S.A., Binder, A., Müller, E. and Kloft, M., 2018, July. Deep one-class classification. In International conference on machine learning (pp. 4393-4402). PMLR. |
| [28] | Scholkopf, B., Platt, J.C., Shawe-Taylor, J., Smola, A.J. and Williamson, R.C., 2001. Estimating the support of a high-dimensional distribution. Neural Computation, 13(7), pp.1443-1471. |
| [29] | Shyu, M.L., Chen, S.C., Sarinnapakorn, K. and Chang, L., 2003. A novel anomaly detection scheme based on principal component classifier. MIAMI UNIV CORAL GABLES FL DEPT OF ELECTRICAL AND COMPUTER ENGINEERING. |
| [30] | Tang, J., Chen, Z., Fu, A.W.C. and Cheung, D.W., 2002, May. Enhancing effectiveness of outlier detections for low density patterns. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 535-548. Springer, Berlin, Heidelberg. |
| [31] | Wang, X., Du, Y., Lin, S., Cui, P., Shen, Y. and Yang, Y., 2019. adVAE: A self-adversarial variational autoencoder with Gaussian anomaly prior knowledge for anomaly detection. Knowledge-Based Systems. |
| [32] | Zhao, Y. and Hryniewicki, M.K. XGBOD: Improving Supervised Outlier Detection with Unsupervised Representation Learning. IEEE International Joint Conference on Neural Networks, 2018. |
| [33] | Zhao, Y., Nasrullah, Z., Hryniewicki, M.K. and Li, Z., 2019, May. LSCP: Locally selective combination in parallel outlier ensembles. In Proceedings of the 2019 SIAM International Conference on Data Mining (SDM), pp. 585-593. Society for Industrial and Applied Mathematics. |
| [34] | Zhao, Y., Hu, X., Cheng, C., Wang, C., Wan, C., Wang, W., Yang, J., Bai, H., Li, Z., Xiao, C., Wang, Y., Qiao, Z., Sun, J. and Akoglu, L. (2021). SUOD: Accelerating Large-scale Unsupervised Heterogeneous Outlier Detection. Conference on Machine Learning and Systems (MLSys). |