The JEE Main 2022 June 29 – Shift 2 Maths Question Paper with Solutions are given on this page. The JEE Main 2022 answer keys help students to evaluate their performance in the JEE Main 2022 exam. The JEE Main 2022 question paper solutions can also be downloaded in PDF format for free. They have been accurately prepared by our subject experts. The JEE Main 2022 question papers and solutions help students to grasp the concepts in an easy way. Check out the JEE Main 2022 June 29 – Shift 2 Maths Question Paper with Solutions given below.
JEE Main 2022 June 29 Second Shift Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let α be a root of the equation 1 + x2 + x4 = 0. Then the value of α1011 + α2022 – α3033 is equal to
(A) 1
(B) α
(C) 1 + α
(D) 1 + 2α
Answer (A)
Sol. 1 + x2 + x4 = 0
Root is ω(cube root of unity)
ω1011 + ω2022 – ω3033
= (ω3)337 + (ω3)674 – (ω3)1011
= 1 + 1 – 1 = 1
2. Let arg(z) represent the principal argument of the complex number z. Then, |z| = 3 and arg(z – 1) – arg(z + 1) = π/4 intersect
(A) exactly at one point
(B) exactly at two points
(C) nowhere
(D) at infinitely many points
Answer (C)
Sol.
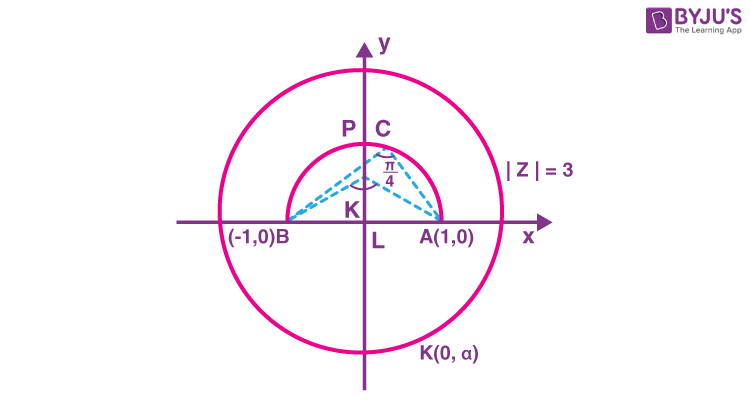
|z| = 3
arg(z – 1) – arg(z + 1) = π/4
\(\begin{array}{l}\angle AKL=\angle ACB=\frac{\pi}{4}\end{array} \)
⇒ LK = AL = α = 1
K(0, 1)
\(\begin{array}{l}\text{Radius}= \sqrt{2}\end{array} \)
\(\begin{array}{l}PL = PK + KL = \sqrt{2} +1\end{array} \)
\(\begin{array}{l}P(0, 1 +\sqrt{2})\end{array} \)
Number of intersection = 0
3. Let \(\begin{array}{l}A = \begin{bmatrix}2 & -1 \\0 & 2 \\\end{bmatrix}\end{array} \)
If B = I – 5C1(adjA) + 5C2(adjA)2 – …. – 5C5(adjA)5, then the sum of all elements of the matrix B is
(A) –5
(B) –6
(C) –7
(D) –8
Answer (C)
Sol.
\(\begin{array}{l}A=\left[\begin{array}{cc}2 & -1 \\ 0 & 2\end{array}\right] \Rightarrow \operatorname{adj}(A)\left[\begin{array}{ll}2 & 1 \\ 0 & 2\end{array}\right]\end{array} \)
B = I – 5C1(adjA) + 5C2(adjA)2 + ….. + 5C5(adjA)5
\(\begin{array}{l}=(I-adjA)^5=\left(\left[\begin{array}{ll}1 & 0 \\0 & 1\end{array}\right]-\left[\begin{array}{ll}2 & 1 \\0 & 2\end{array}\right]\right)^{5}=\left[\begin{array}{cc}-1 & -1 \\0 & 1\end{array}\right]^{5}\end{array} \)
Let
\(\begin{array}{l}P=\left[\begin{array}{cc}-1 & -1 \\ 0 & -1\end{array}\right] \Rightarrow B=P^{5}\end{array} \)
\(\begin{array}{l}P^{2} =\left[\begin{array}{cc}-1 & -1 \\0 & -1\end{array}\right] \left[\begin{array}{cc}-1 & -1 \\0 & -1\end{array}\right]=\left[\begin{array}{ll}1 & 2 \\0 & 1\end{array}\right]\end{array} \)
\(\begin{array}{l}P^{3} =\left[\begin{array}{ll}1 & 2 \\0 & 1\end{array}\right]\left[\begin{array}{cc}-1 & -1 \\0 & -1\end{array}\right]=\left[\begin{array}{cc}-1 & -3 \\0 & -1\end{array}\right] \end{array} \)
\(\begin{array}{l}P^{4} =\left[\begin{array}{cc}-1 & -3 \\0 & -1\end{array}\right]\left[\begin{array}{cc}-1 & -1 \\0 & -1\end{array}\right]=\left[\begin{array}{ll}1 & 4 \\0 & 1\end{array}\right] \end{array} \)
\(\begin{array}{l}P^{5} =\left[\begin{array}{ll}1 & 4 \\0 & 1\end{array}\right]\left[\begin{array}{cc}-1 & -1 \\0 & -1\end{array}\right]=\left[\begin{array}{cc}-1 & -5 \\0 & 1\end{array}\right]=B\end{array} \)
Sum of elements = –1 –5 – 1 + 0 = –7
4. The sum of the infinite series
\(\begin{array}{l}1+\frac{5}{6}+\frac{12}{6^{2}}+\frac{22}{6^{3}}+\frac{35}{6^{4}}+\frac{51}{6^{5}}+\frac{70}{6^{6}}+\ldots . .\end{array} \)
is equal to
\(\begin{array}{l}(A)\ \frac{425}{216}\end{array} \)
\(\begin{array}{l}(B)\ \frac{429}{216}\end{array} \)
\(\begin{array}{l}(C)\ \frac{288}{125}\end{array} \)
\(\begin{array}{l}(D)\ \frac{280}{125}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}S=1+\frac{5}{6}+\frac{12}{6^{2}}+\frac{22}{6^{3}}+\ldots\end{array} \)
\(\begin{array}{l}\frac{1}{6}S=\frac{1}{6}+\frac{5}{6^{2}}+\frac{12}{6^{3}}+\ldots\end{array} \)
\(\begin{array}{l}\frac{5 S}{6}=1+\frac{4}{6}+\frac{7}{6^{2}}+\frac{10}{6^{3}}+\frac{13}{6^{4}}+\ldots\end{array} \)
\(\begin{array}{l}\frac{5 S}{36}=\frac{1}{6}+\frac{4}{6^{2}}+\frac{7}{6^{3}}+\frac{10}{6^{4}}+\ldots\end{array} \)
\(\begin{array}{l}\frac{25 S}{36}=1+\frac{3}{6}+\frac{3}{6^{2}}+\frac{3}{6^{3}}+\frac{3}{6^{4}}+\ldots\end{array} \)
\(\begin{array}{l}\frac{25 S}{36}=1+\frac{\frac{3}{6}}{1-\frac{1}{6}}\end{array} \)
\(\begin{array}{l}\frac{25 S}{36}=\frac{8}{5}\end{array} \)
\(\begin{array}{l}S=\frac{288}{125}\end{array} \)
5. The value of \(\begin{array}{l}\lim _{x \rightarrow 1} \frac{\left(x^{2}-1\right) \sin ^{2}(\pi x)}{x^{4}-2 x^{3}+2 x-1}\end{array} \)
is equal to
\(\begin{array}{l}(A)\ \frac{\pi^{2}}{6}\end{array} \)
\(\begin{array}{l}(B)\ \frac{\pi^{2}}{3}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\pi^{2}}{2}\end{array} \)
\(\begin{array}{l}(D)\ \pi^{2}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\lim _{x \rightarrow 1} \frac{\left(x^{2}-1\right) \sin ^{2} \pi x}{x^{4}-2 x^{3}+2 x-1}\end{array} \)
\(\begin{array}{l}=\lim _{x \rightarrow 1} \frac{(x+1)(x-1) \sin ^{2} \pi x}{(x-1)^{3}(x+1)}\end{array} \)
Let x – 1 = t
\(\begin{array}{l}\lim _{t \rightarrow 0} \frac{(2+t) t \sin ^{2} \pi t}{t^{3}(t+2)} =\lim _{t \rightarrow 0}\frac{\sin ^{2} \pi t}{\pi^{2} t^{2}} \cdot \pi^{2}= \pi^{2}\end{array} \)
6. Let f : R → R be a function defined by;
\(\begin{array}{l}f(x)=(x-3)^{n_{1}}(x-5)^{n_{2}}, n_{1}, n_{2} \in N\end{array} \)
Then, which of the following is NOT true?
(A) For n1 = 3, n2 = 4, there exists α ∈ (3, 5) where f attains local maxima.
(B) For n1 = 4, n2 = 3, there exists α ∈ (3, 5) where f attains local minima.
(C) For n1 = 3, n2 = 5, there exists α ∈ (3, 5) where f attains local maxima.
(D) For n1 = 4, n2 = 6, there exists α ∈ (3, 5) where f attains local maxima.
Answer (C)
Sol. For n2 ∈ odd, there will be local minima in (3, 5)
for n2 ∈ even, there will be local maxima in (3, 5)
7. Let f be a real valued continuous function on [0, 1] and \(\begin{array}{l}f(x)=x+\int_{0}^{1}(x-t) f(t) d t\end{array} \)
Then, which of the following points (x, y) lies on the curve y = f(x)?
(A) (2, 4)
(B) (1, 2)
(C) (4, 17)
(D) (6, 8)
Answer (D)
Sol.
\(\begin{array}{l}f(x)=x \int_{0}^{1}(x-t) f(t) d t\end{array} \)
\(\begin{array}{l}f(x)=x+x \int_{0}^{1} f(t) d t-\int_{0}^{1} t f(t) d t\end{array} \)
\(\begin{array}{l}f(x)=x\left(1+\int_{0}^{1} f(t) d t\right)-\int_{0}^{1} t f(t) d t\end{array} \)
Let
\(\begin{array}{l}1+\int_{0}^{1} f(t) d t=a\ \text{and}\ \int_{0}^{1} t f(t) d t=1\end{array} \)
f(x) = ax – b
Now,
\(\begin{array}{l}a=1+\int_{0}^{1}(a t-b) d t=1+\frac{a}{2}-b \Rightarrow \frac{a}{2}+b=1\end{array} \)
\(\begin{array}{l}b=\int_{0}^{1} t(a t-b) d t=\frac{a}{3}-\frac{b}{2} \Rightarrow \frac{3 b}{2}=\frac{a}{3} \Rightarrow b=\frac{2 a}{9}\end{array} \)
\(\begin{array}{l}\frac{a}{2}+\frac{2 a}{9}=1\end{array} \)
\(\begin{array}{l}\Rightarrow a=\frac{18}{13} \quad b=\frac{4}{13}\end{array} \)
\(\begin{array}{l}f(x)=\frac{18 x-4}{13}\end{array} \)
(6, 8) lies on f(x) i.e. option (D)
8. If \(\begin{array}{l}\int_{0}^{2}\left(\sqrt{2 x}-\sqrt{2 x-x^{2}}\right) d x=\int_{0}^{1}\left(1-\sqrt{1-y^{2}}-\frac{y^{2}}{2}\right) d y+\int_{1}^{2}\left(2-\frac{y^{2}}{2}\right) d y+I\end{array} \)
then I equal is
\(\begin{array}{l}(A)\ \int_{0}^{1}\left(1+\sqrt{1-y^{2}}\right) d y\end{array} \)
\(\begin{array}{l}(B)\ \int_{0}^{1}\left(\frac{y^{2}}{2}-\sqrt{1-y^{2}}+1\right) d y\end{array} \)
\(\begin{array}{l}(C)\ \int_{0}^{1}\left(1-\sqrt{1-y^{2}}\right) d y\end{array} \)
\(\begin{array}{l}(D)\ \int_{0}^{1}\left(\frac{y^{2}}{2}+\sqrt{1-y^{2}}+1\right) d y\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\int_{0}^{2} \sqrt{2 x} d x-\int_{0}^{2} \sqrt{1-(x-1)^{2}} d x=\int_{0}^{2}\left(1-\frac{y^{2}}{2}\right) d y-\int_{0}^{1} \sqrt{1-y^{2}} dy+1+l\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{8}{3}-2 \int_{0}^{1} \sqrt{1-y^{2}} d y=\frac{2}{3}+1-\int_{0}^{1} \sqrt{1-y^{2}} d y+l\end{array} \)
\(\begin{array}{l}\Rightarrow I=1-\int_{0}^{1} \sqrt{1-y^{2}} d y\end{array} \)
\(\begin{array}{l}\Rightarrow I=\int_{0}^{1}\left(1-\sqrt{1-y^{2}}\right) d y\end{array} \)
9. If y = y (x) is the solution of the differential equation \(\begin{array}{l}\left(1+e^{2 x}\right) \frac{d y}{d x}+2\left(1+y^{2}\right) e^{x}=0\end{array} \)
and y(0) = 0, then \(\begin{array}{l}6\left(y^{\prime}(0)+\left(y\left(\log _{e} \sqrt{3}\right)\right)^{2}\right)\end{array} \)
is equal to
(A) 2
(B) –2
(C) –4
(D) –1
Answer (C)
Sol.
\(\begin{array}{l}\left(1+e^{2 x}\right) \frac{d y}{d x}+2\left(1+y^{2}\right) e^{x}=0\end{array} \)
\(\begin{array}{l}\int \frac{d y}{1+y^{2}}=-\int \frac{2 e^{x}}{1+e^{2 x}} d x \quad \begin{aligned}&e^{x}=t \\&e^{x} d x=d t\end{aligned}\end{array} \)
\(\begin{array}{l}\tan ^{-1} y=-2 \int \frac{d t}{1+t^{2}}\end{array} \)
\(\begin{array}{l}\tan ^{-1} y=2 \tan ^{-1}\left(e^{x}\right)+c\end{array} \)
\(\begin{array}{l}y(0) \Rightarrow c=\frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\tan ^{-1} y=-2 \tan ^{-1}\left(e^{x}\right)+\frac{\pi}{2}\end{array} \)
\(\begin{array}{l}y=\cot \left(2 \tan ^{-1} e^{x}\right)\end{array} \)
\(\begin{array}{l}\frac{d y}{d x}=-\operatorname{cosec}^{2}\left(2 \tan ^{-1} e^{x}\right)\left(\frac{2 e^{x}}{1+e^{2 x}}\right)\end{array} \)
\(\begin{array}{l}y^{\prime}(0)=\left.\frac{d y}{d x}\right|_{x=0}=\frac{-2}{2}=-1\end{array} \)
\(\begin{array}{l}y=\cot \left(2 \tan ^{-1} e^{x}\right)\end{array} \)
\(\begin{array}{l}y(\ln \sqrt{3})=\cot \left(2 \tan ^{-1} e^{\log e^{\sqrt{3}}}\right)\end{array} \)
\(\begin{array}{l}=\cot \left(2 \tan ^{-1} \sqrt{3}\right)=\cot \left(\frac{2 \pi}{3}\right)=-\cot \frac{\pi}{3}=-\frac{1}{\sqrt{3}}\end{array} \)
\(\begin{array}{l}6\left(y^{\prime}(0)+(y(\ln \sqrt{3}))^{2}\right)=6\left(-1+\left(-\frac{1}{\sqrt{3}}\right)^{2}\right)=6\left(-1+\frac{1}{3}\right)=-4\end{array} \)
10. Let P : y2 = 4ax, a > 0 be a parabola with focus S. Let the tangents to the parabola P make an angle of π/4 with the line y = 3x + 5 touch the parabola P at A and B. Then the value of a for which A, B and S are collinear is
(A) 8 only
(B) 2 only
\(\begin{array}{l}(C)\ \frac{1}{4}~\text{only}\end{array} \)
(D) any a > 0
Answer (D)
Sol.
\(\begin{array}{l}P:y^2=4ax,a >{0}~~~~S(a,0)\end{array} \)
Equation of tangent on parabola
\(\begin{array}{l}y=m x+\frac{a}{m}\end{array} \)
\(\begin{array}{l}y=3 x+5\end{array} \)
\(\begin{array}{l}\tan \frac{\pi}{4}=\left|\frac{m-3}{1+3 m}\right| \Rightarrow m-3=\pm(1+3 m)\end{array} \)
m – 3 = 1 + 3m
m = – 2
m – 3 = –1 – 3m
\(\begin{array}{l}m=\frac{1}{2}\end{array} \)
\(\begin{array}{l}\text{Equation of one tangent :}y=-2 x-\frac{a}{2}\end{array} \)
\(\begin{array}{l}\text{Equation of other tangent :}y=\frac{x}{2}+2a\end{array} \)
Point of contact are
\(\begin{array}{l}\left(\frac{a}{(-2)^{2}}, \frac{-2 a}{(-2)}\right) \text{and} \left(\frac{a}{\left(\frac{1}{2}\right)^{2}}, \frac{-2 a}{\frac{1}{2}}\right)\end{array} \)
\(\begin{array}{l}A\left(\frac{a}{4}, a\right)\ \text{and}\ B(4 a,-4 a)\end{array} \)
\(\begin{array}{l}\text{Now or} (\Delta ABS)=0 [S ~\text{is the focus}]\end{array} \)
\(\begin{array}{l}\frac{1}{2}\left|\begin{array}{ccc}\frac{a}{4} & a & 1 \\ 4 a & -4 a & 1 \\ a & 0 & 1\end{array}\right|=0\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{a}{4}(-4 a-0)-a(4 a-a)+1\left(0-\left(-4 a^{2}\right)\right)=0\end{array} \)
\(\begin{array}{l}=-a^{2}-3 a^{2}+4 a^{2}=0\end{array} \)
Always true
11. Let a triangle ABC be inscribed in the circle \(\begin{array}{l}x^{2}-\sqrt{2}(x+y)+y^{2}=0\end{array} \)
such that ∠BAC= π/2. If the length of side AB is √2, then the area of the ΔABC is equal to :
\(\begin{array}{l}(A)\ (\sqrt{2}+\sqrt{6}) / 3\end{array} \)
\(\begin{array}{l}(B)\ (\sqrt{6}+\sqrt{3}) / 2\end{array} \)
\(\begin{array}{l}(C)\ (3+\sqrt{3}) / 4\end{array} \)
\(\begin{array}{l}(D)\ (\sqrt{6}+2 \sqrt{3}) / 4\end{array} \)
Answer (Dropped)
Sol.
\(\begin{array}{l}x^{2}-\sqrt{2} x-\sqrt{2} y+y^{2}=0\end{array} \)
\(\begin{array}{l}\text{Centre}=\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\end{array} \)
Radius = 1
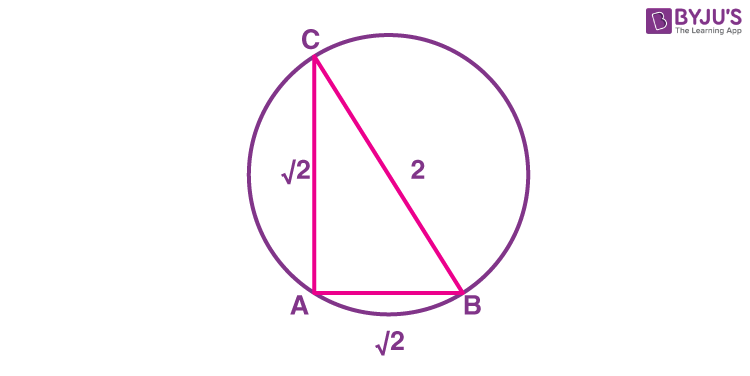
BC is diameter
\(\begin{array}{l}\operatorname{ar}(\triangle A B C)=\frac{1}{2} \times \sqrt{2} \times \sqrt{2}=1\end{array} \)
12. Let \(\begin{array}{l}\frac{x-2}{3}=\frac{y+1}{-2}=\frac{z+3}{-1}\end{array} \)
lie on the plane px – qy + z = 5, for some p, q ∈ ℝ. The shortest distance of the plane from the origin is :
\(\begin{array}{l}(A)\ \sqrt{\frac{3}{109}}\end{array} \)
\(\begin{array}{l}(B)\ \sqrt{\frac{5}{142}}\end{array} \)
\(\begin{array}{l}(C)\ \frac{5}{\sqrt{71}}\end{array} \)
\(\begin{array}{l}(D)\ \frac{1}{\sqrt{142}}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}\frac{x-2}{3}=\frac{y+1}{-2}=\frac{z+3}{-1}=\lambda\end{array} \)
\(\begin{array}{l}(3 \lambda+2,-2 \lambda-1,-\lambda-3)\text{lies on plane}~ px – qy+z=5\end{array} \)
\(\begin{array}{l}p(3 \lambda+2)-q(-2 \lambda-1)+(-\lambda-3)=5\end{array} \)
\(\begin{array}{l}\lambda(3 p+2 q-1)+(2 p+q-8)=0\end{array} \)
3p + 2q – 1 = 0
2p + q – 8 = 0
Solving these two equations, p = 15, q = -22
Equation of plane
\(\begin{array}{l}15 x+22 y+z-5=0\end{array} \)
Shortest distance from origin
\(\begin{array}{l}=\frac{|0+0+0-5|}{\sqrt{15^{2}+22^{2}+1}}\end{array} \)
\(\begin{array}{l}=\frac{5}{\sqrt{710}}\end{array} \)
\(\begin{array}{l}=\sqrt{\frac{5}{142}}\end{array} \)
13. The distance of the origin from the centroid of the triangle whose two sides have the equations
x – 2y + 1 = 0 and 2x – y – 1 = 0 and whose orthocenter is (7/3, 7/3) is :
(A) √2
(B) 2
(C) 2√2
(D) 4
Answer (C)
Sol.
\(\begin{array}{l}\left.\begin{array}{l}A B: x-2 y+1=0 \\ A C: 2 x-y-1=0\end{array}\right\} A(1,1)\end{array} \)
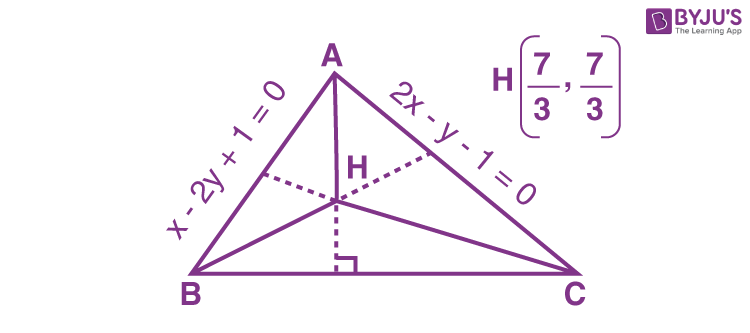
\(\begin{array}{l} \text {Altitude from B is}~ BH=x+2 y-7=0 \Rightarrow B(3,2)\end{array} \)
\(\begin{array}{l}\text{Altitude from C is}\ CH=2 x+y-7=0\Rightarrow C(2,3)\end{array} \)
\(\begin{array}{l} \text {Centroid of} ~\triangle ABC=G(2,2) O G=2 \sqrt{2}\end{array} \)
14. Let Q be the mirror image of the point P(1, 2, 1) with respect to the plane x + 2y + 2z = 16. Let T be a plane passing through the point Q and contains the line \(\begin{array}{l}\vec{r}=-\hat{k}+\lambda(\hat{i}+\hat{j}+2 \hat{k}), \lambda \in \mathbb{R}\end{array} \)
. Then, which of the following points lies on T?
(A) (2, 1, 0)
(B) (1, 2, 1)
(C) (1, 2, 2)
(D) (1, 3, 2)
Answer (B)
Sol. P(1, 2, 1) image in plane x + 2y + 2z = 16
\(\begin{array}{l}\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-1}{2}=\frac{-2(1+2 \times 2+2 \times 1-16)}{1^{2}+2^{2}+2^{2}}\end{array} \)
\(\begin{array}{l}\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-1}{2}=2\end{array} \)
Q(3, 6, 5)
\(\begin{array}{l}\vec{r}=-\hat{k}+\lambda(\hat{i}+\hat{j}+2 \hat{k})\end{array} \)
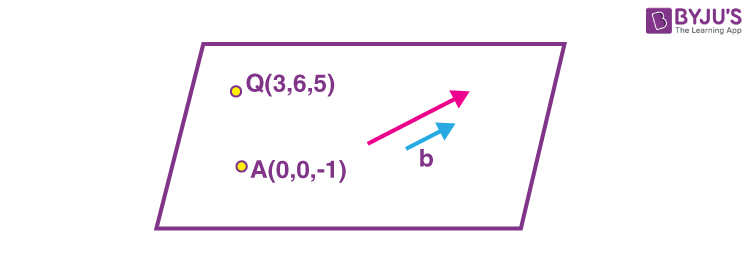
\(\begin{array}{l}A Q=3 \hat{i}+6 \hat{j}+6 \hat{k}\end{array} \)
\(\begin{array}{l}=3(\hat{i}+2 \hat{j}+2 \hat{k})\end{array} \)
\(\begin{array}{l}\vec{n}=(\hat{i}+2 \hat{j}+2 \hat{k}) \times(\hat{i}+\hat{j}+2 \hat{k})\end{array} \)
\(\begin{array}{l}\left|\begin{array}{lll}\hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 2 \\ 1 & 1 & 2\end{array}\right|\end{array} \)
\(\begin{array}{l}=2 \hat{i}-0 \hat{j}-\hat{k}\end{array} \)
Equation of plane ≡ 2(x – 0) + 0 (y – 0) – 1 (z + 1) = 0
2x – z = 1
Point lying on plane from the option is (1, 2, 1) i.e., option (B)
15. Let A, B, C be three points whose position vectors respectively are
\(\begin{array}{l}\vec{a}=\hat{i}+4 \hat{j}+3 \hat{k}\end{array} \)
\(\begin{array}{l}\vec{b}=2 \hat{i}+\alpha \hat{j}+4 \hat{k}, \alpha \in \mathbb{R}\end{array} \)
\(\begin{array}{l}\vec{c}=3 \hat{i}-2 \hat{j}+5 \hat{k}\end{array} \)
\(\begin{array}{l}\text{If}\ \alpha\ \text{ is the smallest positive integer for which}\ \vec{a}, \vec{b}, \vec{c}\end{array} \)
are non collinear, then the length of the median, in ΔABC, through A is:
\(\begin{array}{l}(A)\ \frac{\sqrt{82}}{2}\end{array} \)
\(\begin{array}{l}(B)\ \frac{\sqrt{62}}{2}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\sqrt{69}}{2}\end{array} \)
\(\begin{array}{l}(D)\ \frac{\sqrt{66}}{2}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}\overrightarrow{A B} \| \overrightarrow{A C}\end{array} \)
if
\(\begin{array}{l}\frac{1}{2}=\frac{\alpha-4}{-6}=\frac{1}{2}\end{array} \)
⇒ α = 1
\(\begin{array}{l}\vec{a}, \vec{b}, \vec{c}\ \text{are non-collinear for}\ \alpha = 2\end{array} \)
(smallest positive integer)
Mid point of BC
\(\begin{array}{l}=M\left(\frac{5}{2}, 0, \frac{9}{2}\right)\end{array} \)
\(\begin{array}{l}A M=\sqrt{\frac{9}{4}+16+\frac{9}{4}}=\frac{\sqrt{82}}{2}\end{array} \)
16. The probability that a relation R from {x, y} to {x, y} is both symmetric and transitive, is equal to
(A) 5/16
(B) 9/16
(C) 11/16
(D) 13/16
Answer (A)
Sol. Total number of relations
\(\begin{array}{l}=2^{2^{2}}=2^{4}=16\end{array} \)
Relations which are symmetric as well as transitive are
φ, {(x, x)}, {(y, y)}, {(x, x), (x, y), (y, y), (y, x)}, {(x, x), (y, y)}
\(\begin{array}{l}\therefore \text{Favourable cases} = 5\end{array} \)
\(\begin{array}{l}\therefore P_r = \frac{5}{16}\end{array} \)
17. The number of values of a ∈ N such that the variance of 3, 7, 12, a, 43 – a is a natural number is :
(1) 0
(2) 2
(3) 5
(4) Infinite
Answer (A)
Sol.
\(\begin{array}{l}\text{Mean}=\frac{3+12+7+a+43-a}{5}=13\end{array} \)
\(\begin{array}{l}\text{Variance} =\frac{9+49+144+a^{2}+(43-a)^{2}}{5}-13^{2}\in \text{Natural number}\end{array} \)
\(\begin{array}{l}\frac{2 a^{2}-a+1}{5} \in \textup{Natural number} \end{array} \)
\(\begin{array}{l}2a^2-a+1=5n ~~~~~[n\in N]\end{array} \)
\(\begin{array}{l}2a^2-a+1-5n=0\end{array} \)
D = 1 – 4(1 – 5n)2
= 40n – 7
D cannot be a perfect square as all perfect squares will be of the form of 4λ or 4λ + 1
So, a cannot be natural number
∴ Number of values = 0
18. From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of the tower. Then the height of the tower is :
(A) 15√3
(B) 20√3
(C) 20 + 10√3
(D) 30
Answer (D)
Sol.
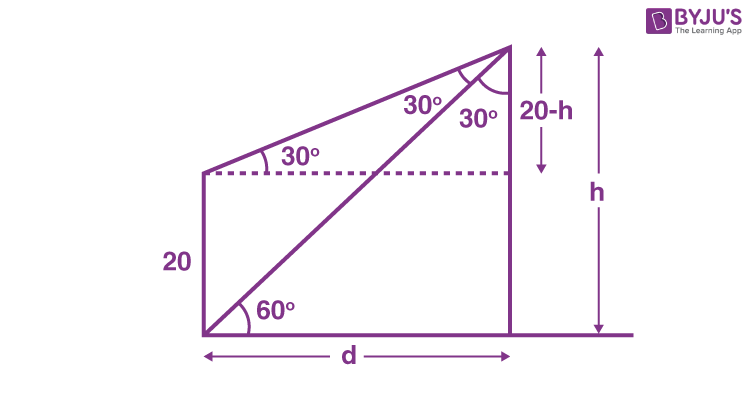
\(\begin{array}{l}\tan 60^{\circ}=\frac{h}{d} \quad \tan 30^{\circ}=\frac{20-h}{d}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{20-h}{h / \sqrt{3}}=\frac{1}{\sqrt{3}} \Rightarrow \frac{2 h}{3}=20 \Rightarrow h=30 \mathrm{~m}\end{array} \)
19. Negation of the Boolean statement (p ∨ q) ⇒ ((~ r) ∨ p) is equivalent to
(A) p ∧ (~ q) ∧ r
(B) (~ p) ∧ (~ q) ∧ r
(C) (~p) ∧ q ∧ r
(D) p ∧ q ∧ (~ r)
Answer (C)
Sol. p ∨ q ⇒ (~ r ∨ p)
≡ ~ (p ∨ q) ∨ (~ r ∨ p)
≡ (~ p ∧ ~ q) ∨ (p ∨ ~ r)
≡ [(~ p ∨ p) ∧ (~ q ∨ p)] ∨ ~ r
≡ (~ q ∨ p) ∨ ~ r
Its negation is ~ p ∧ q ∧ r.
20. Let n ≥ 5 be an integer. If 9n – 8n – 1 = 64α and 6n – 5n – 1 = 25β, then α – β is equal to
\(\begin{array}{l}(A)\ 1+{ }^{n} C_{2}(8-5)+{ }^{n} C_{3}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-1}-5^{n-1}\right)\end{array} \)
\(\begin{array}{l}(B)\ 1+{ }^{n} C_{3}(8-5)+{ }^{n} C_{4}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-2}-5^{n-2}\right)\end{array} \)
\(\begin{array}{l}(C)\ { }^{n} C_{3}(8-5)+{ }^{n} C_{4}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-2}-5^{n-2}\right)\end{array} \)
\(\begin{array}{l}(D)\ { }^{n} C_{4}(8-5)+{ }^{n} C_{5}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-3}-5^{n-3}\right)\end{array} \)
Answer (C)
Sol. (1 + 8)n – 8n – 1 = 64α
\(\begin{array}{l}\Rightarrow 1+8 n+{ }^{n} C_{2} 8^{2}+{ }^{n} C_{3} 8^{3}+\ldots+{ }^{n} C_{n} 8^{n}-8 n-1= 64 \alpha\end{array} \)
\(\begin{array}{l}\Rightarrow \alpha={ }^{n} C_{2}+{ }^{n} C_{3} 8+{ }^{n} C_{4} 8{ }^{2}+\ldots+{ }^{n} C_{n} 8^{n-2} \ldots \text { (1) }\end{array} \)
Similarly
(1 + 5)n – 5n – 1 = 25β
\(\begin{array}{l}\Rightarrow 1+5 n+{ }^{n} C_{2} 5^{2}+{ }^{n} C_{3} 5^{3}+\ldots+{ }^{n} C_{n} 5^{n}-5 n-1= 25\beta\end{array} \)
\(\begin{array}{l}\Rightarrow \beta={ }^{n} C_{2}+{ }^{n} C_{3} \cdot 5+{ }^{n} C_{4} \cdot 5^{2}+\ldots+{ }^{n} C_{n} 5^{n-2} \ldots(2)\end{array} \)
\(\begin{array}{l}\alpha-\beta={ }^{n} C_{3}(8-5)+{ }^{n} C_{4}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-2}-5^{n-2}\right) \end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse andw the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let \(\begin{array}{l}\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}, \vec{b}=\hat{i}-\hat{j}+\hat{k}\ and\ \vec{c}\end{array} \)
be a vector such that \(\begin{array}{l}\vec{a}+(\vec{b} \times \vec{c})=\overrightarrow{0}\ \text{and}\ \vec{b} \cdot \vec{c}=5.\end{array} \)
\(\begin{array}{l}\text{Then the value of}\ 3(\vec{c} \cdot \vec{a})\ \text{is equal to}——.\end{array} \)
Answer (10*)
Sol. Data not correct
\(\begin{array}{l}\because \vec{a} \cdot \vec{b}=1-2+3=2~~~~~\left\{\text {according~to}~ \vec{a}~and~\vec{b} \right \}\end{array} \)
but given that
\(\begin{array}{l}\vec{a}+(\vec{b} \times \vec{c})=\overrightarrow{0}\end{array} \)
\(\begin{array}{l}\vec{a}=-(\vec{b} \times \vec{c})\end{array} \)
\(\begin{array}{l}\Rightarrow \vec{a} \perp \vec{b} \text { and } \vec{a} \perp \vec{c}-\end{array} \)
\(\begin{array}{l}\therefore \vec{a} \cdot \vec{b}=0\end{array} \)
{Contradicts}
2. Let y = y(x), x > 1, be the solution of the differential equation\(\begin{array}{l}(x-1) \frac{d y}{d x}+2 x y=\frac{1}{x-1}\ \text{with}\ y(2)=\frac{1+e^{4}}{2 e^{4}}.\ \text{If}\ y(3)=\frac{e^{\alpha}+1}{\beta e^{\alpha}},\end{array} \)
then the value of α + β is equal to ____.
Answer (14)
Sol.
\(\begin{array}{l}\frac{d y}{d x}+y\left(\frac{2 x}{x-1}\right)=\frac{1}{(x-1)^{2}}\end{array} \)
\(\begin{array}{l}\text { I.F } =e^{\int \frac{2 x}{x-1} d x} \end{array} \)
\(\begin{array}{l}=e^{2 \int\left(\frac{x-1}{x-1}+\frac{1}{x-1}\right) d x}\end{array} \)
\(\begin{array}{l}=e^{2 x+2 \ln (x-1)}\end{array} \)
\(\begin{array}{l}=e^{2x}(x-1)^2\end{array} \)
\(\begin{array}{l}\Rightarrow \int d\left(y \cdot e^{2 x}(x-1)^{2}\right)=\int e^{2 x} d x\end{array} \)
\(\begin{array}{l}\Rightarrow y \cdot e^{2 x}(x-1)^{2}=\frac{e^{2 x}}{2}+c\end{array} \)
\(\begin{array}{l}\downarrow y(2)=\frac{1+e^{4}}{2 e^{4}}\end{array} \)
\(\begin{array}{l}\frac{1+e^{4}}{2 e^{4}} \cdot e^{4}=\frac{e^{4}}{2}+c\end{array} \)
\(\begin{array}{l}\Rightarrow c=\frac{e^{4}}{2}\left(\frac{1+e^{4}-e^{4}}{e^{4}}\right)=\frac{1}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow y \cdot e^{2 x}(x-1)^{2}=\frac{e^{2 x}+1}{2}\end{array} \)
\(\begin{array}{l}\downarrow y(3)=\frac{e^{\alpha}+1}{\beta e^{\alpha}}\end{array} \)
\(\begin{array}{l}\Rightarrow \quad \frac{e^{\alpha}+1}{\beta e^{\alpha}} \cdot e^{6} \cdot 4=\frac{e^{6}+1}{2}\end{array} \)
⇒ α = 6 and β = 8 ⇒ α + β = 14
3. Let 3, 6, 9, 12, … upto 78 terms and 5, 9, 13, 17, … upto 59 terms be two series. Then, the sum of terms common to both the series is equal to _____.
Answer (2223)
Sol. S1 : 3, 6, 9, 12,……78-terms
S2 : 5, 9, 13, 17,…….59-terms
Common terms are 9, 21,……….
T78 of S1 = 3 + (77).3 = 234
T59 of S2 = 5 + (58) 4 = 237
So nth common term ≤ 234
⇒ 9 + (n – 1) 12 ≤ 234
\(\begin{array}{l}\Rightarrow n<\frac{225}{12}+1\end{array} \)
\(\begin{array}{l}\Rightarrow n<\frac{237}{12} \Rightarrow n=19\end{array} \)
S19 of common terms
\(\begin{array}{l}=\frac{19}{2}[2(9)+18.12]\end{array} \)
= 19 (9 + 108)
= 117 × 19 = 2223
4. The number of solutions of the equation sin x = cos2 x in the interval (0, 10) is _____.
Answer (4)
Sol. sinx = 1 – sin2x
⇒ sin2x + sinx – 1 = 0
\(\begin{array}{l}\Rightarrow \sin x=\frac{-1 \pm \sqrt{5}}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow \sin x=\frac{-1+\sqrt{5}}{2}\end{array} \)
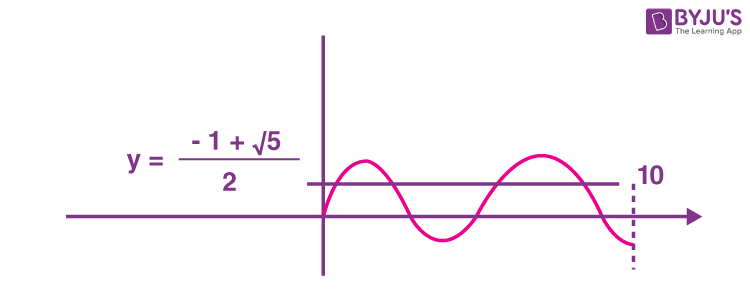
4 solutions
5. For real number a, b (a > b > 0), let
Area \(\begin{array}{l}\left\{(x, y): x^{2}+y^{2} \leq a^{2}\right.$ and $\left.\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} \geq 1\right\}=30 \pi\end{array} \)
and
\(\begin{array}{l} \text{Area} \left\{(x, y): x^{2}+y^{2} \geq b^{2}\right.$ and $\left.\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} \leq 1\right\}=18 \pi\end{array} \)
Then the value of (a – b)2 is equal to _____.
Answer (12)
Sol.
\(\begin{array}{l}x^{2}+y^{2} \leq a^{2} ~\text{is interior of circle} ~\text{and} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} \geq 1 ~ \text{is exterior of ellipse}\end{array} \)
 ∴ Area = πa2 – πab = 30π …(1)
∴ Area = πa2 – πab = 30π …(1)
\(\begin{array}{l} \text{Similarly}~ x^{2}+y^{2} \geq b^{2} \text~{and}~ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} \leq 1~\text {gives} \end{array} \)
πab – πb2 = 18π …(2)
\(\begin{array}{l} \text{By~(1) and (2)}, \frac{a}{b}=\frac{5}{3} \Rightarrow a=\frac{5b}{3}\end{array} \)
\(\begin{array}{l}\Rightarrow \pi \cdot \frac{25 b^{2}}{9}-\pi \cdot \frac{5 b^{2}}{3}=30 \pi\end{array} \)
\(\begin{array}{l}\Rightarrow \left(\frac{25}{9}-\frac{5}{3}\right) b^{2}=30\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{10}{9} b^{2}=30 \Rightarrow b^{2}=27\end{array} \)
\(\begin{array}{l} \text{and}~a^{2}=\frac{25}{9} \cdot 27=75\end{array} \)
\(\begin{array}{l}(a-b)^{2}=(5 \sqrt{3}-3 \sqrt{3})^{2}=3 \cdot 4=12\end{array} \)
6. Let f and g be twice differentiable even functions on (–2, 2) such that \(\begin{array}{l}f\left(\frac{1}{4}\right)=0, f\left(\frac{1}{2}\right)=0, f(1)=1~\text{and}~ g\left(\frac{3}{4}\right)=0, g(1)=2\end{array} \)
. Then, the minimum number of solutions of f(x)g′′(x) + f′(x)g′(x) = 0 in (–2, 2) is equal to_____.
Answer (4)
Sol. Let h(x)=f(x)· g’(x)
As f(x) is even
\(\begin{array}{l}f\left(\frac{1}{2}\right)=\left(\frac{1}{4}\right)=0\end{array} \)
\(\begin{array}{l}\Rightarrow f\left(-\frac{1}{2}\right)=f\left(-\frac{1}{4}\right)=0\end{array} \)
and g(x) is even ⇒ g′(x) is odd
and g(1) = 2 ensures one root of g′(x) is 0.
So, h(x) = f(x) . g′(x) has minimum five zeroes
∴ h′(x) = f′(x) · g′(x) + f(x) · g′′(x)= 0,
has minimum 4 zeroes
7. Let the coefficients of x–1 and x–3 in the expansion of \(\begin{array}{l}\left(2 x^{\frac{1}{5}}-\frac{1}{x^{\frac{1}{5}}}\right)^{15}, x>0\end{array} \)
be m and n respectively. If r is a positive integer such that \(\begin{array}{l}m n^{2}={ }^{15} C_{r} \cdot 2^{r}\end{array} \)
then the value of r is equal to ______.
Answer (5)
Sol.
\(\begin{array}{l}T_{r+1}={ }^{15} C_{r}\left(2 x^{1 / 5}\right)^{15-r}\left(\frac{-1}{x^{1 / 5}}\right)^{r}\end{array} \)
\(\begin{array}{l} \text{For coefficient of}~ x^{-1}\\\frac{15-r}{5}-\frac{r}{5}=-1 \Rightarrow 15-2 r=-5 \Rightarrow r=10\end{array} \)
\(\begin{array}{l}\therefore m={}^{15}C_{10}.2^5\end{array} \)
\(\begin{array}{l}\text{and for coefficient of}~ x^{-3}~~~~~15-2r=-15\Rightarrow r=15\\ \therefore n = -{}^{15}C_{15}\end{array} \)
\(\begin{array}{l}\text{Given }m n^{2} = { }^{15} C_{r} \cdot 2^{r}\end{array} \)
\(\begin{array}{l}\Rightarrow { }^{15} C_{10} \cdot 2^{5}={ }^{15} C_{r} \cdot 2^{r}\\ \Rightarrow r = 5\end{array} \)
8. The total number of four digit numbers such that each of first three digits is divisible by the last digit, is equal to _______.
Answer (1086)
Sol. If unit digit is 1 then → 9 ×s 10 × 10 = 900 numbers
If unit digit is 2 then → 4 × 5 × 5 = 100 numbers
If unit digit is 3 then → 3 × 4 × 4 = 48 numbers
If unit digit is 4 then → 2 × 3 × 3 = 18 numbers
If unit digit is 5 then → 1 × 2 × 2 = 4 numbers
If unit digit is 6 then → 1 × 2 × 2 = 4 numbers
For 7, 8, 9 → 4 + 4 + 4 = 12 Numbers
Total = 1086 Numbers
9. Let \(\begin{array}{l}M=\left[\begin{array}{cc}0 & -\alpha \\ \alpha & 0\end{array}\right]\end{array} \)
where α is a non-zero real number an \(\begin{array}{l}N=\sum_{k=1}^{49} M^{2 k}.\ \text{If}\ \left(I-M^{2}\right) N=-2 I\end{array} \)
then the positive integral value of α is ____ .
Answer (1)
Sol.
\(\begin{array}{l}M=\left[\begin{array}{cc}0 & -\alpha \\ \alpha & 0\end{array}\right], M^{2}=\left[\begin{array}{cc}-\alpha^{2} & 0 \\ 0 & -\alpha^{2}\end{array}\right]=-\alpha^{2}I\end{array} \)
\(\begin{array}{l}N=M^{2}+M^{4}+\ldots+M^{98}\\=\left[-\alpha^{2}+\alpha^{4}-\alpha^{6}+\ldots\right]I\\=\frac{-\alpha^{2}\left(1-\left(-\alpha^{2}\right)^{49}\right)}{1+\alpha^{2}}\cdot I\end{array} \)
\(\begin{array}{l}I-M^{2}=\left(1+\alpha^{2}\right) I\\\left(I-M^{2}\right) N=-\alpha^{2}\left(\alpha^{98}+1\right)=-2\\ \therefore \alpha=1\end{array} \)
10. Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x and
g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ____________ .
Answer (18)
Sol. f(g(x)) = 8x2 – 2x
g(f(x)) = 4x2 + 6x + 1
let f(x) = cx2 + dx + e
g(x) = ax + b
f(g(x)) = c(ax + b)2 + d(ax + b) + e ≡ 8x2 – 2x
g(f(x)) = a(cx2 + dx + e) + b ≡ 4x2 + 6x + 1
∴ ac = 4 ad = 6 ae + b = 1
a2c = 8 2abc + ad = –2 cb2 + bd + e = 0
By solving
a = 2 b = –1
c = 2 d = 3 e = 1
∴ f(x) = 2x2 + 3x +1
g(x) = 2x – 1
f(2) + g(2) = 2(2)2 + 3(2) + 1 + 2(2) – 1
= 18
JEE Main Question Paper & Solutions – June 29th 2022 Shift 2
JEE Main 2022 June 29 Shift 2 Question Paper – Physics Solutions
JEE Main 2022 June 29 Shift 2 Question Paper – Chemistry Solutions
JEE Main 2022 June 29 Shift 2 Question Paper – Maths Solutions
Frequently Asked Questions – FAQs
Q1
How many questions are there in the JEE Main 2022 June 29 Shift 2 Maths question paper?
There are 30 questions in the JEE Main 2022 June 29 Shift 2 Maths question paper.
Q2
What is the difficulty level of the JEE Main 2022 Shift 2 June 29 Maths question paper?
The difficulty level of the JEE Main 2022 Shift 2 June 29 Maths question paper is 1.9 out of 3.
Q3
Which topic was covered from the chapter Application of Integrals in the JEE Main 2022 Maths Shift 2 June 29 question paper?
The topic Area under the curves was covered from the chapter Application of Integrals.
Q4
How was the Shift 2 JEE Main 2022 June 29 Maths question paper?
The Shift 2 JEE Main 2022 June 29 Maths question paper was of moderate difficulty. It had 5 easy questions, 13 medium questions and 3 difficult questions as per the memory-based question paper.
Q5
Was there any question from Straight lines in the JEE Main 2022 Shift 2 June 29 Maths question paper?
Yes. There was a medium-level question from Straight lines in the JEE Main 2022 Shift 2 June 29 Maths question paper.






 ∴ Area = πa2 – πab = 30π …(1)
∴ Area = πa2 – πab = 30π …(1)











Comments